 |
Главная |
Дифференциальные уравнения второго порядка, которые допускают понижение порядка
|
из
5.00
|
Рассмотрим самые простые случаи дифференциальных уравнений второго порядка, которые допускают понижение порядка.
1. Самым простым уравнением такого вида является уравнение:
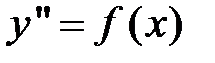 ,
,
то есть уравнение, правая часть которого зависит лишь от независимой переменной 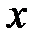 . Проинтегрировав левую и праву части уравнения, получим
. Проинтегрировав левую и праву части уравнения, получим 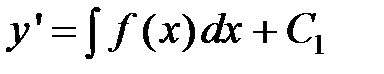 , где
, где 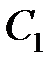 – произвольная интегрирования.
– произвольная интегрирования.
Таким образом, дифференциальное уравнение второго порядка имеет множество решений. Как отмечено выше, чтобы найти частное решение части, необходимо удовлетворить начальным условиям, то есть определить произвольные 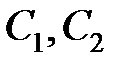
Пример 1. 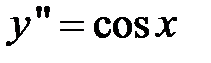 .
.
Решение. Поскольку 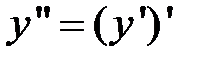 , то
, то 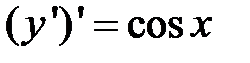 , то есть
, то есть 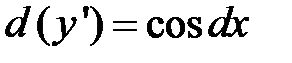 . Тогда
. Тогда 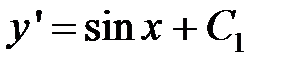 . Таким образом
. Таким образом 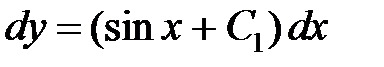 .
.
Проинтегрировав обе части полученного выражения, мы получим общее решение начального уравнения: 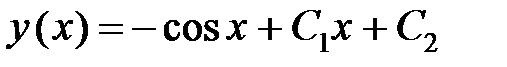 .
.
Пример 2. Найти частное решение 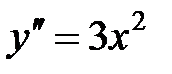 , которое удовлетворяет начальным условиям
, которое удовлетворяет начальным условиям 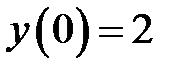 ,
, 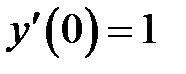 .
.
Решение.
Сначала ищем общее решение. Нужно последовательно проинтегрировать данное уравнение. Принимая во внимание, что 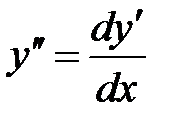 имеем
имеем 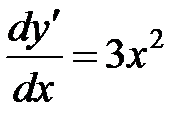 или
или 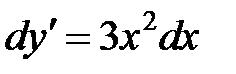 . Берем интеграл от обеих частей
. Берем интеграл от обеих частей
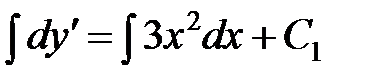 или
или 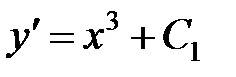
то есть 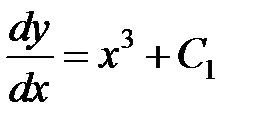
Умножим на 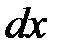 обе части уравнения
обе части уравнения 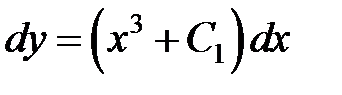 . Интегрируем
. Интегрируем
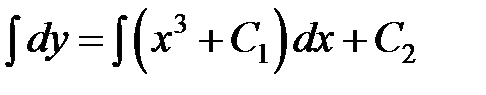 ,
, 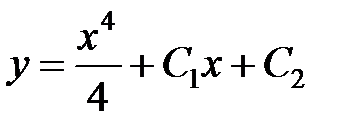 .
.
Теперь нужно найти 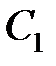 и
и 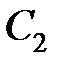 учитывая начальные условия. По условию
учитывая начальные условия. По условию 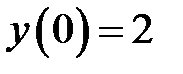 и
и 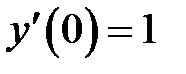 тогда
тогда
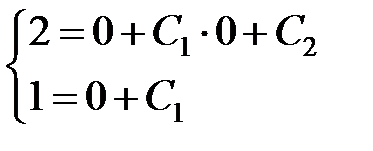 .
.
Следовательно  ,
, 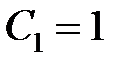 . Тогда
. Тогда 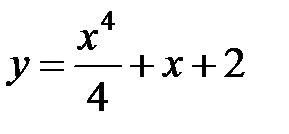 или
или 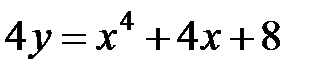 .
.
2. Дифференциальное уравнение, которое допускает понижение порядка, вида: 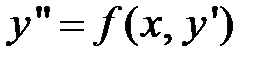 .
.
Правая часть уравнения не содержит в себе неизвестную функцию. В этом случае уравнение может быть решено с помощью подстановки:
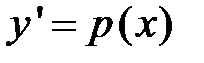 ,
, 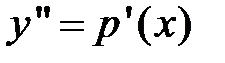 .
.
В результате применения этой подстановки уравнение принимает вид:  , то есть его порядок снижается. Следовательно, имеем дифференциальное уравнение первого порядка.
, то есть его порядок снижается. Следовательно, имеем дифференциальное уравнение первого порядка.
Пример 3. 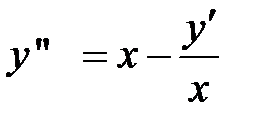 .
.
Решение. Поскольку уравнение не содержит в себе неизвестную функцию 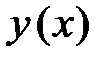 , то для его решения используем подстановку:
, то для его решения используем подстановку: 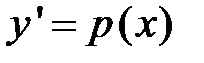 и
и 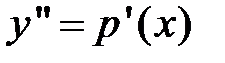 . Тогда получим:
. Тогда получим: 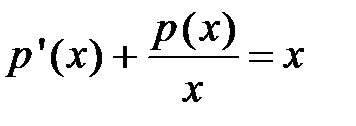 .
.
Сделаем замену 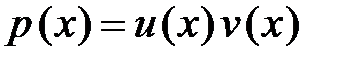 :
: 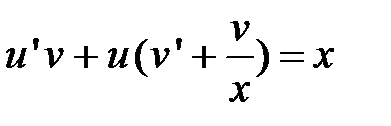 .
.
Приравняв выражение, которое стоит в последнем уравнении в скобках, к нулю, мы получим: 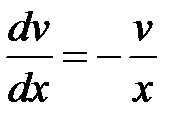 или
или 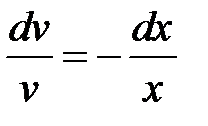 .
.
Проинтегрировав левую и праву части последнего соотношения получим: 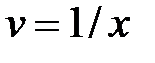 . Следовательно, для нахождения неизвестной функции
. Следовательно, для нахождения неизвестной функции 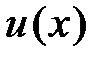 имеем дифференциальное уравнение:
имеем дифференциальное уравнение:
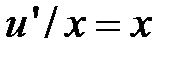 , то есть
, то есть 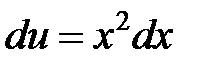 .
.
Таким образом, функция 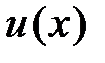 равна:
равна: 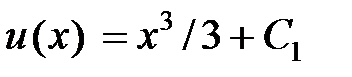 . Теперь найдем функцию
. Теперь найдем функцию 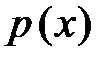 :
: 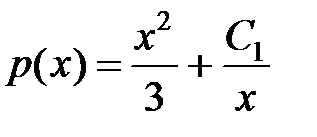 .
.
Поскольку 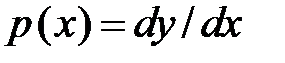 , то имеем:
, то имеем: 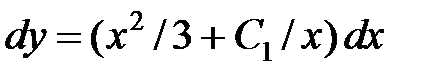 .
.
Далее проинтегрировав обе части последнего уравнения, получим окончательное решение начального уравнения:
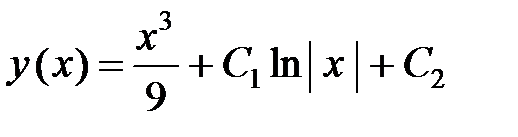 .
.
Пример 4. Найти общее решение 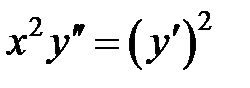 .
.
Решение. Применяем замену 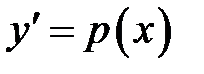 , откуда
, откуда 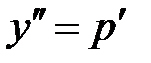 . После этого данное уравнение приобретает вид:
. После этого данное уравнение приобретает вид: 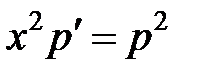 . Получили уравнение с разделяемыми переменными
. Получили уравнение с разделяемыми переменными 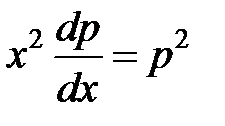 или
или 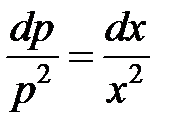 .
.
Берем интеграл от обеих частей 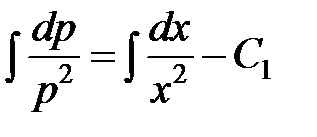 ,
,
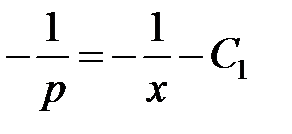 или
или 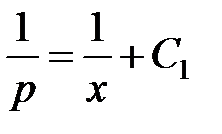 ,
, 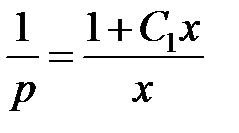 . Откуда
. Откуда 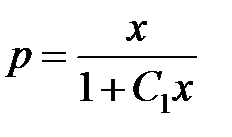 .
.
Учитывая, что 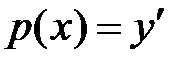 имеем
имеем 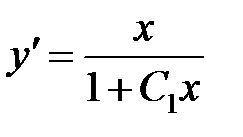 или
или 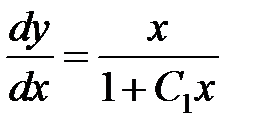 , следовательно
, следовательно 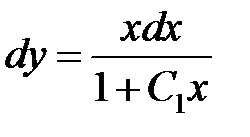 .
.
Интегрируем обе части последнего равенства 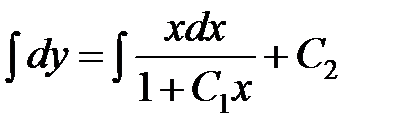 .
.
Для нахождения 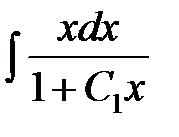 нужно выделить целую часть, потому что подинтегральная функция есть неправильная рациональная дробь. Для этого нужно разделить числитель на знаменатель.
нужно выделить целую часть, потому что подинтегральная функция есть неправильная рациональная дробь. Для этого нужно разделить числитель на знаменатель.
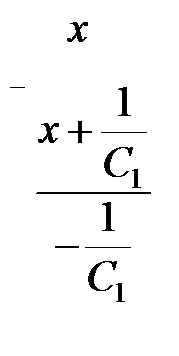
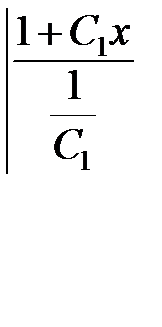 .
.
Интеграл принимает вид
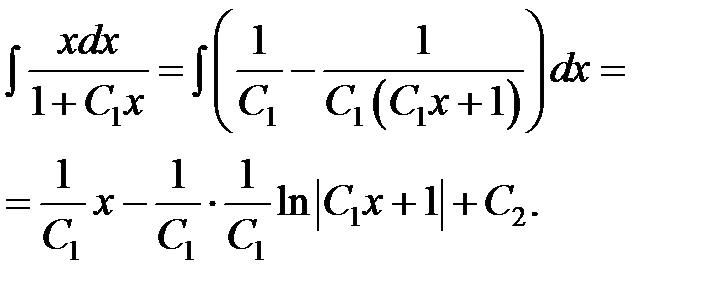
Таким образом 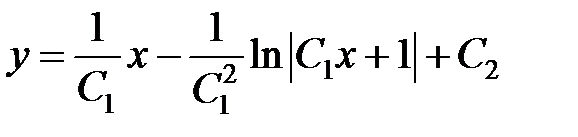 ,
,
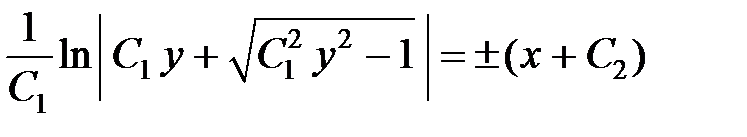 .
.
3. Уравнение, которое не содержит явно аргумент: 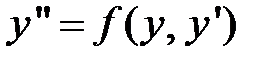 . Правая часть уравнения в этом случае не содержит в себе независимую переменную
. Правая часть уравнения в этом случае не содержит в себе независимую переменную 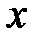 и решение можно получить с помощью подстановки:
и решение можно получить с помощью подстановки:
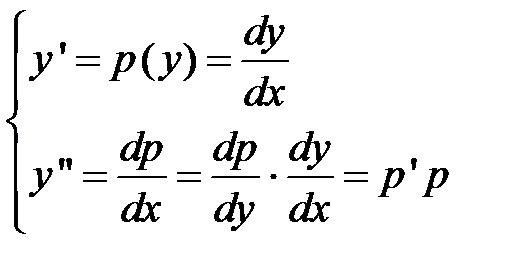 .
.
Подставляя неизвестную функцию 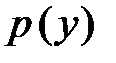 и ее производную
и ее производную 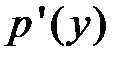 в начальное уравнение, получим дифференциальное уравнение первого порядка относительно
в начальное уравнение, получим дифференциальное уравнение первого порядка относительно 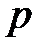 как функции от
как функции от 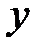 :
:
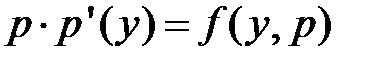 .
.
Пример 5. 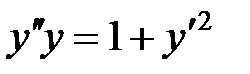 .
.
Решение.
Обозначив 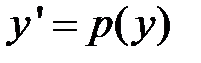 и
и 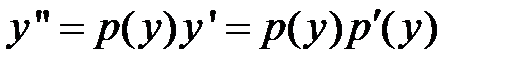 и подставив эти выражения в начальное уравнение, получим:
и подставив эти выражения в начальное уравнение, получим: 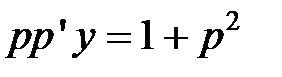 – дифференциальное уравнение с разделяемыми переменными. Отделив переменные, получим:
– дифференциальное уравнение с разделяемыми переменными. Отделив переменные, получим: 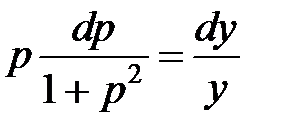 .
.
Отсюда: 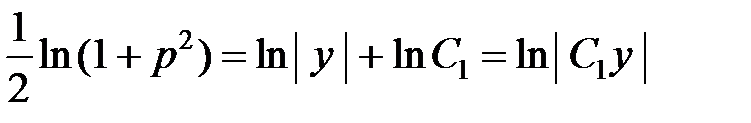 ,
,
или 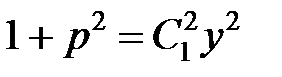 ,
, 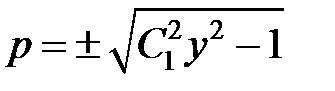 , или
, или 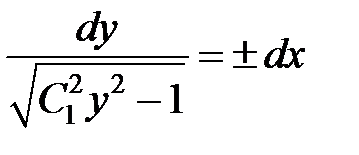 .
.
Проинтегрировав обе части полученного уравнения, получим общий интеграл начального дифференциального уравнения:
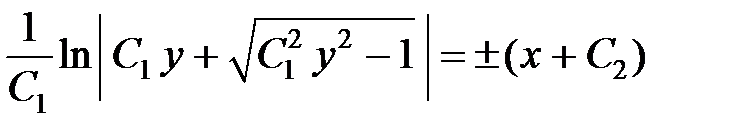 .
.
|
из
5.00
|
Обсуждение в статье: Дифференциальные уравнения второго порядка, которые допускают понижение порядка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

