 |
Главная |
Теорема Абеля. Радиус сходимости степенного ряда
|
из
5.00
|
Степенным рядом называется ряд:
 , (15.1)
, (15.1)
членами которого являются степенные функции 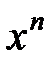 с возрастающими целыми показателями, числа
с возрастающими целыми показателями, числа 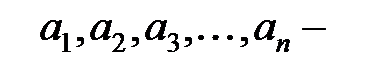 коэффициенты данного ряда. Виражение
коэффициенты данного ряда. Виражение 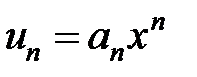 – общий член степенного ряда.
– общий член степенного ряда.
Иногда рассматривают степенной ряд более общего вида:
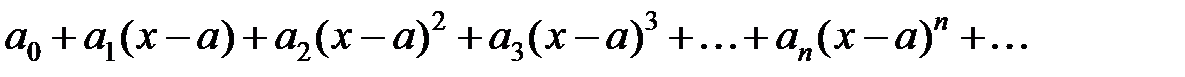 (15.2)
(15.2)
Этот ряд легко привести к предыдущему, если считать 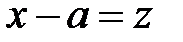 .
.
Областью сходимости степенного ряда называется множество значений  , при которых степенной ряд сходится.
, при которых степенной ряд сходится.
Теорема Абеля. Если степенной ряд сходится для некоторого значения 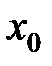 , не равного нулю, то он сходится абсолютно для всех значений
, не равного нулю, то он сходится абсолютно для всех значений 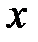 , для которых выполняется условие:
, для которых выполняется условие:
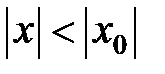 . (15.3)
. (15.3)
Если степенной ряд расходится для некоторого значения 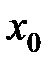 , то он расходитсяся для всех значений
, то он расходитсяся для всех значений 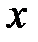 , для которых выполняется условие:
, для которых выполняется условие:
 . (15.4)
. (15.4)
Из теоремы Абеля вытекает, что для произвольного степенного ряда существует положительное число 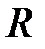 (конечное или бесконечное), такое, что для всех
(конечное или бесконечное), такое, что для всех 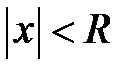 ряд сходится, причем абсолютно, а при
ряд сходится, причем абсолютно, а при 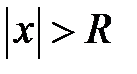 ряд расходится.
ряд расходится.
Интервал 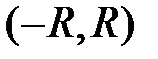 , во всех точках которого степенной ряд сходится, а в точках, которые не принадлежат данному интервалу, степенной ряд расходится называется интервалом сходимости данного ряда.
, во всех точках которого степенной ряд сходится, а в точках, которые не принадлежат данному интервалу, степенной ряд расходится называется интервалом сходимости данного ряда.
Половина интервала сходимости называется радиусом сходимости степенного ряда. Если 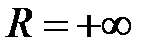 , то интервал сходимости составляет всю числовую ось
, то интервал сходимости составляет всю числовую ось 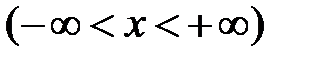 . Если
. Если 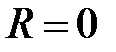 , то степенной ряд сходится лишь при
, то степенной ряд сходится лишь при 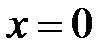 , то есть интервал сходимости вырождается в точку.
, то есть интервал сходимости вырождается в точку.
Для решения вопроса о сходимости степенного ряда применяют признак Даламбера к ряду, который составлен из абсолютных величин его членов, то есть вычисляют предел:
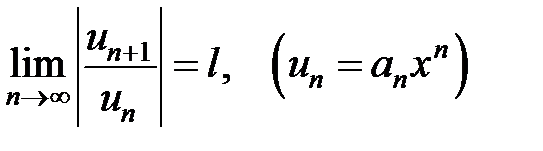
и сравниваю ее с единицей.
Множество значений 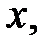 для которых
для которых 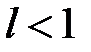 , образует область абсолютной сходимости степенного ряда (15.1). Множество значений
, образует область абсолютной сходимости степенного ряда (15.1). Множество значений 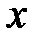 , для которых
, для которых 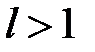 , образует область расходимости.
, образует область расходимости.
Следовательно,
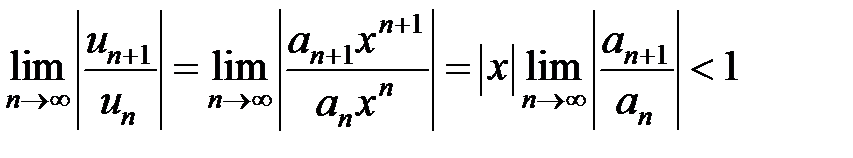 , а
, а 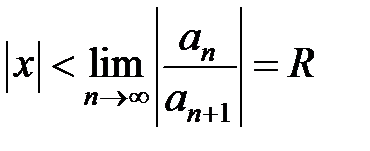 ,
,
где 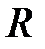 – радиус сходимости степенного ряда.
– радиус сходимости степенного ряда.
То есть, 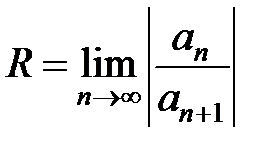 . (15.5)
. (15.5)
Пример 1. Найти область сходимости степенного ряда  .
.
Решение.
Обозначим 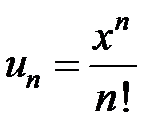 , тогда
, тогда  . Дальше получаем:
. Дальше получаем:
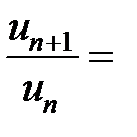
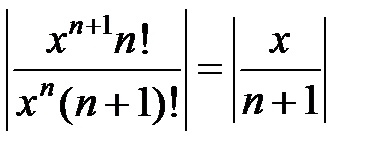 .
.
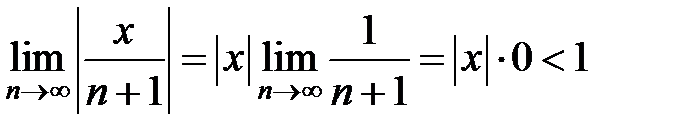 .
.
Последнее неравенство выполняется для любого 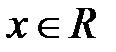 , то есть ряд сходится на всей числовой оси:
, то есть ряд сходится на всей числовой оси: 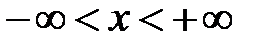 .
.
Можно сразу найти 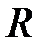 , поскольку степенной ряд содержит все степени
, поскольку степенной ряд содержит все степени 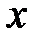 :
:
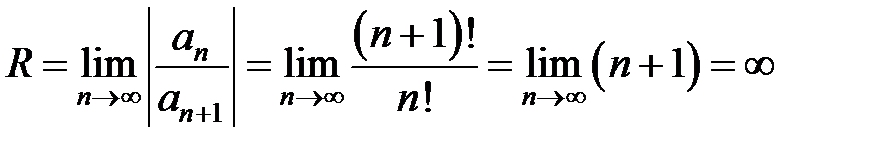 .
.
Таким образом, ряд сходится на всей числовой оси.
Пример 2. Найти область сходимости степенного ряда 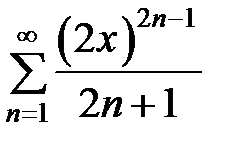 .Решение.
.Решение.
В этом степенном ряду коэффициенты при четных степенях 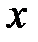 равны нулю, то есть
равны нулю, то есть 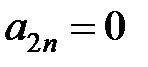 . Непосредственное применение признака Даламбера дает:
. Непосредственное применение признака Даламбера дает:
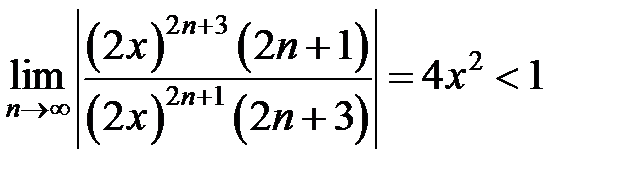 ,
,
откуда получаем, что 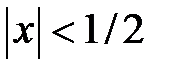 , следовательно
, следовательно 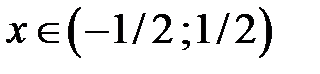 .
.
Исследуем поведение степенного ряда на концах интервала сходимости.
Пусть 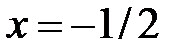 . Подставим это значение в степенной ряд и получим числовой ряд:
. Подставим это значение в степенной ряд и получим числовой ряд:
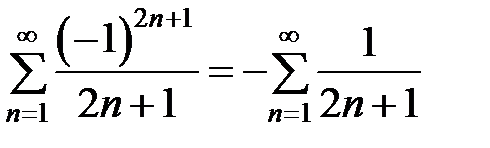 ,
,
поведение которого определяется поведением гармоничного ряда. Следовательно этот ряд расходящийся по признаку сравнения в предельной форме.
Пусть 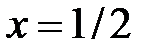 . При этом значении
. При этом значении 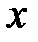 степенной ряд превращается в числовой ряд:
степенной ряд превращается в числовой ряд: 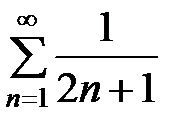 . Этот ряд, как уже было показано, является расходящимся.
. Этот ряд, как уже было показано, является расходящимся.
Таким образом, область сходимости ряда является интервалом 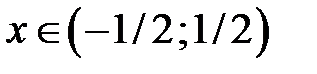 .
.
Пример 3. Найти область сходимости ряда 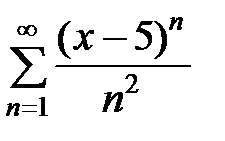 .
.
Решение.
Обозначим 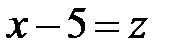 . Следовательно
. Следовательно 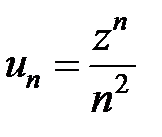 – степенной ряд.
– степенной ряд.
Тогда  .
.
Для нахождения радиуса сходимости теперь можно применить формулу:
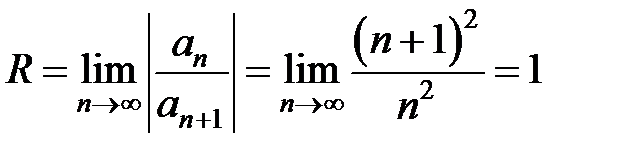 .
.
Исследуем поведение ряда на концах полученного интервала.
При 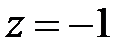 получим числовой ряд:
получим числовой ряд: 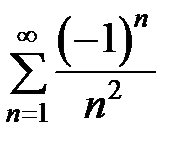 . Этот ряд сходится согласно признаку Лейбница.
. Этот ряд сходится согласно признаку Лейбница.
При 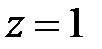 числовой ряд имеет вид:
числовой ряд имеет вид:  . Он сходится, как ряд Дирихле при
. Он сходится, как ряд Дирихле при 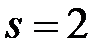 .
.
Следовательно, областью сходимости ряда будет промежуток 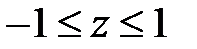 . Возвращаясь к переменной
. Возвращаясь к переменной 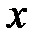 , получим
, получим 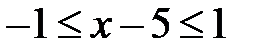 , или
, или  .
.
Таким образом, областью сходимости данного ряда является промежуток 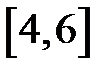 .
.
|
из
5.00
|
Обсуждение в статье: Теорема Абеля. Радиус сходимости степенного ряда |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

