 |
Главная |
Вопрос 1. Векторное произведение векторов
|
из
5.00
|
(геометрический смысл, свойства).
Векторы  ,
,  и
и  , взятые в указанном порядке, образуют правую тройку векторов (рис. 2), если
, взятые в указанном порядке, образуют правую тройку векторов (рис. 2), если  находится по ту сторону плоскости, содержащей векторы
находится по ту сторону плоскости, содержащей векторы  и
и  , откуда кратчайший поворот от вектора
, откуда кратчайший поворот от вектора  к
к  можно совершить против часовой стрелки.
можно совершить против часовой стрелки.

В противном случае векторы образуют левую тройку векторов (рис. 1).
Векторным произведением векторов  и
и  называется вектор
называется вектор 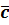 =
= 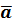 ×
×  , удовлетворяющей следующим 3‒м свойствам:
, удовлетворяющей следующим 3‒м свойствам:
1. │  │ = │
│ = │  │·│
│·│  │· sina, гдеa = Ð(
│· sina, гдеa = Ð(  ;
;  ).
).
2.  ⊥
⊥  ;
;  ⊥
⊥  ;
;
3. Векторы  ,
,  и
и  , взятые в указанном порядке, образуют правую тройку векторов.
, взятые в указанном порядке, образуют правую тройку векторов.
Геометрический смысл.

Sпароаллелограмма = │  │·│
│·│  │· sina => │
│· sina => │  │ =│
│ =│  ×
×  │,
│,
т.е. │ 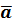 ×
×  │= Sпароаллелограмма
│= Sпароаллелограмма
Модуль векторного произведения векторов  и
и  равен Sпараллелограмма, построенного на векторах ‒ множителях.
равен Sпараллелограмма, построенного на векторах ‒ множителях.
Свойства векторного произведения.
1.  ×
×  = ‒ (
= ‒ (  ×
×  ) –не коммутативно
) –не коммутативно
2. Если  коллинеарен
коллинеарен  , то
, то  ×
×  =
=  , т. к. sin 00 = 0.
, т. к. sin 00 = 0.
3. l (  ×
×  ) = (l ·
) = (l ·  ) ×
) ×  =
=  × (l ·
× (l ·  ) – ассоциативность
) – ассоциативность
4. (  +
+  ) ×
) ×  =
=  ×
×  +
+  ×
×  – дистрибутивность
– дистрибутивность
Вопрос 2. Выражение векторного произведения через координаты.
Пусть  = (
= (  );
);  = (
= (  );
);
Разложим а и b по базисным векторам:
а= x1i + y1 j + z1k, b = x2i + y2 j + z2k.
Используя свойства векторного произведения, получаем
 ×
×  = (x1i + y1 j+ z1k)× (x2i + y2 j+ z2k) =
= (x1i + y1 j+ z1k)× (x2i + y2 j+ z2k) =
= x1·x2·i×i + x1·y2·i×j + x1·z2·i×k +
+ y1·x2 j×i + y1·y2 j; j + y1·z2 j×k +
+ z1·x2 k×i + z1·y2 k×j + z1·z2 k×k. (1)
По определению векторного произведения находим
i×i = 0, i×j = k, i×k= –j,
j×i = –k, j×j = 0, j×k = i,
k×i = j,k×j = –i. k×k = 0.
Учитывая эти равенства, формулу (1) можно записать так:
 ×
×  = x1y2k–x1z2 j–y1x2k + y1z2 i + z1x2 j –z1y2i
= x1y2k–x1z2 j–y1x2k + y1z2 i + z1x2 j –z1y2i
или
 ×
×  = (y1z2 –z1y2) i + (z1x2 –x1z2 )j + (x1y2–y1x2) k. (2)
= (y1z2 –z1y2) i + (z1x2 –x1z2 )j + (x1y2–y1x2) k. (2)
Формула (2) дает выражение для векторного произведения двух векторов, заданных своими координатами.
Полученную формулу можно записать в другом более удобном для запоминания виде:
 ×
×  =
=  (3)
(3)
Обычно формулу (3) записывают еще короче:
 ×
×  =
=  (4)
(4)
‒ формула для вычисления векторного произведения.
Тогда,
Sпароаллелограмма = │ 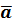 ×
×  │=
│= 
Sтреугольника =  =
=  ;
;
Пример:найти векторное произведение векторов:

Решение:


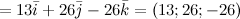
Вопрос 3. Смешанное произведение векторов
(геометрический смысл, свойства).
Смешанным произведением векторов (  ×
×  )
)  называется скалярное произведение вектора(
называется скалярное произведение вектора(  ×
×  ) на вектор
) на вектор  .
.
Геометрический смысл
Построим на векторах  ,
,  параллелепипед и найдем его объем V.
параллелепипед и найдем его объем V.

Vпараллелепипеда = Sосн. · H =  ·
· 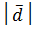 =
=  ·
·  · Cosa=
· Cosa=  .
.
 = Vпараллелепипеда
= Vпараллелепипеда
Модуль смешанного произведениятрех векторов численно равен объему параллелепипеда, построенного на трех данных векторах ‒ множителях.
Vтетраэдра =  Vпараллелепипеда
Vпараллелепипеда
|
из
5.00
|
Обсуждение в статье: Вопрос 1. Векторное произведение векторов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

