 |
Главная |
Построение линии пересечения поверхностей
|
из
5.00
|
Построение линии пересечения двух многогранников. При пересечении поверхностей двух многогранников образуется замкнутая ломаная пространственная линия, состоящая из отрезков прямых. Каждый отрезок представляет собой линию, по которой пересекаются грани многогранников. Вершины ломаной линии представляют собой точки, в которых пересекаются ребра одного многогранника с гранями или ребрами другого.
Построение линии пересечения двух многогранников сводится к построению точек пересечения ребер одного многогранника с гранями второго и ребер второго многогранника с гранями первого (рис. 3.20) .
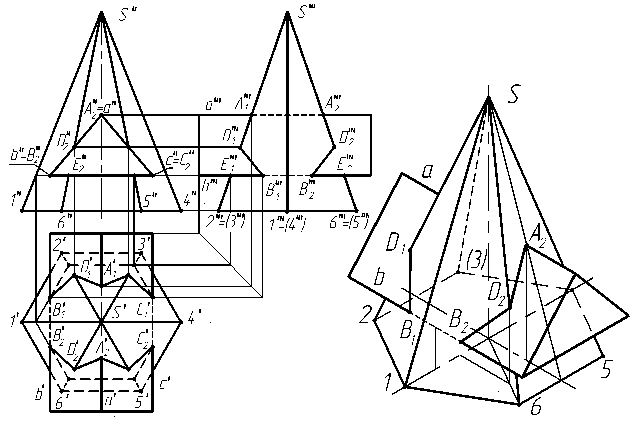
Рис. 3.20
При решении задач на построение линии пересечения призмы и пирамиды вначале анализируют расположение многогранников относительно плоскостей проекций и их взаимное расположение. Трёхгранная призма является фронтально-проецирующей, поэтому линия пересечения на фронтальной проекции совпадёт с проекцией основания призмы, т.е. со сторонами треугольника. Грани пирамиды S23 и S65 - профильно-проецирующие. Некоторые точки, принадлежащие линии пересечения, можно построить, используя только линии проекционной связи, для других необходимы дополнительные построения.
Так, при построении точек пересечения рёбер пирамиды с гранями призмы использовались только линии связи (например, чтобы определить проекции точек D и E пресечения ребра S6 c гранями призмы). Аналогично определяются горизонтальные проекции точек А1 и А2 по известным фронтальной и профильной проекциям. Дополнительные построения необходимы при определении горизонтальных проекций точек В1 и В2 пересечения ребра b призмы с гранями S12 и S16 пирамиды (рис. 3.11а, 3.20).
Построение линии пересечения пирамиды и призмы в изометрии выполнено по известным координатам точек пересечения.
Построение линии пересечения прямого кругового конуса и призмыпоказано на рис. 3.21. Боковая поверхность призмы полностью проходит через боковую поверхность конуса, в результате получаются две замкнутые линии пересечения.

Рис. 3.21
При построении линии пересечения сначала строят характерные точки (обозначены буквами), в которых рёбра призмы пересекаются с поверхностью прямого кругового конуса. Затем строят промежуточные точки линии пересечения (обозначены цифрами).
Аксонометрическая проекция линии пересечения построена по точкам, взятым с чертежа. Поскольку линия пересечения принадлежит обеим поверхностям, то в прямоугольной изометрии она получена исходя из принадлежности точек поверхности призмы, как более простой поверхности.
Пример выполнения графической работы (ГР 3) приведен в прил. 4.
Вопросы для самопроверки
1. Какое положение аксонометрических осей принято в диметрической прямоугольной проекции по ГОСТ 2.317-69?
2. Какое положение аксонометрических осей принято в изометрической прямоугольной проекции по ГОСТ 2.317-69?
3. Что называют коэффициентом искажения по аксонометрическим осям?
4. Какие коэффициенты искажения приняты по осям х, у, z при выполнении прямоугольной изометрии по ГОСТ 2.317-69?
5. Какие коэффициенты искажения приняты по осям х, y, z при выполнении прямоугольной диметрии по ГОСТ 2.317-69?
6. Как выбирают направления больших и малых осей эллипсов при построении аксонометрических изображений окружностей, расположенных в координатных или параллельных им плоскостях?
7. Чему равны большие и малые оси эллипсов при выполнении прямоугольной изометрии без искажения по осям х, у, z?
8. Чему равны большие и малые оси эллипсов при выполнении прямоугольной диметрии без искажения по осям х, y, z?
9. Как наносят линии штриховки сечений в аксонометрических прямоугольных проекциях?
|
из
5.00
|
Обсуждение в статье: Построение линии пересечения поверхностей |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

