Тема 1.3. Вычисление основных статистических

Показателей.

Основные понятия теории вероятностей

(тема рассмотрена в курсе «Основы высшей математики»)

П Л А Н

1. События и их виды. Действия над событиями

2. Классическое и статистическое определения вероятности

3. Теоремы сложения и умножения вероятностей

4. Полная вероятность. Формулы Байеса

5. Распределения случайных величин. Функции распределения

6. Основные числовые характеристики распределения случайных величин

7. Вероятностный характер психологических выводов

 

1.В теории вероятностей рассматриваются явления (опыты), которые при одном и том же комплексе начальных условий в зависимости от случайных обстоятельств заканчиваются различными исходами (результатами).

Возможный результат опыта (испытания, измерения, наблюдения) называется событием. Например:

1) опыт - подбрасывание монеты, события – герб;

2) опыт – стрельба, событие – попадание в мишень;

3) опыт – определение уровня тревожности, событие – он не превосходит какого-либо заданного значения.

События обозначаются заглавными буквами латинского алфавита.

Различают следующие виды событий.

Событие называется достоверным в данном опыте, если оно обязательно произойдет.

Событие называется невозможным в данном опыте, если оно не может произойти в этом опыте.

Событие называетсяслучайным в данном опыте, если оно может произойти, а может и не произойти.

Например, событие А «вынуть черный шар» из урны с белыми шарами является невозможным. Если же в урне только черные шары, то оно будет достоверным, и данное событие окажется случайным, если в урне будут находиться и черные, и белые шары. Т.е. некоторые события могут быть и достоверными, и невозможными, и случайными в зависимости от опыта (начальных условий).

Два события называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании (т.е. не могут произойти одновременно). Например: промах и цель при одном выстреле, белый и черный шар при доставании одного шара, герб и решка при подбрасывании монеты.

Несколько событий называются несовместными, если они попарно несовместны.

События называютсясовместными, если появление одного из них не исключает появление другого в этом опыте. Например:1) опыт – подбрасывание кости: А – выпадение четного числа очков, В – выпадение 2-х очков;2)опыт - подбрасывание 2-х монет: А – герб на 1 монете, В – решка на 2-ой.

Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Например: герб и решка при подбрасывании монеты, выпадение четного и нечетного числа очков на кубике, выпадение 1 или 2 и выпадение очков больших 2-х. Т.е. противоположное событие , состоит в том, что А не произойдет.

События называются равновозможными, если нет оснований полагать, что одно является более возможным, чем другие.

Например: при подбрасывании монеты – выпадение герба и решки.

Каждое событие, которое может наступить в результате опыта, называется элементарным событием (исходом).

Например: при подбрасывании кубика – события А_i=«выпадение i очков», где i= ; но не выпадение четного или нечетного числа очков.

Элементарные исходы (события), при которых данное событие наступает, называются благоприятствующими этому событию.

Например: при подбрасывании кубика событию А - «выпадение четного числа очков» благоприятствуют события А_i=«выпадение i очков», где i=2, 4, 6.

 

Если событие А обязательно произойдет при появлении некоторого другого события В , то говорят ,что В представляет частный случай события А (В А).

Пример: событие В – выпадение 2 очков, событие А – выпадение четного числа очков.

Если А В и В А, т.е. А и В в данном опыте могут появиться или не появиться вместе, то их называют равносильными (эквивалентными) и А=В.

Пример: событие А – вызвать Сидорова, Иванова (перечисляются все юноши по фамилиям) к доске, событие В – вызвать юношей.

 

Множество событий А1, А2…Аn называется полной группой событий, если: 1)они попарно несовместны;

2)появление одного и только одного из них является достоверным

событием.

Например: при подбрасывании кубика – события А_i=«выпадение i очков», где i= ; четное и нечетное число очков.

 

 

Рассмотрим действия событий.

Суммой двух событий А и В называется такое событие С, которое состоит в появлении события А или события В (т.е. хотя бы одного из них). Иногда сумму называют объединением событий А и В.

Геометрическая интерпретация на кругах Эйлера:

а) А и В – совместны б) А и В – несовместны

 

А+В А+В

Рис. 1.

Сумма нескольких событий определяется аналогично.

Произведением событий А и В называется такое событие С, которое состоит в осуществлении события А и В одновременно (иногда называют пересечением событий А и В). Если события несовместны, то АхВ – невозможное событие.

АхВ

Рис. 2.

Аналогично определяется произведение нескольких событий.

Разностью событий А и В называется такое событие С, которое состоит в наступлении А, но не в наступлении В.

А и В – совместны А и В – несовместны

А – В А - В

Рис. 3.

 

Например: событие А – выпадение четного числа очков при подбрасывании кубика, В – выпадение числа очков больших 3. Тогда событие С=А+В - выпадение 2, 4, 5 или 6 очков, событие D= АхВ - выпадение 4 или 6 очков, событие Е=А-В - выпадение 2 очков.

Свойства действий: 1) коммутативность А+В=В+А, АхВ=ВхА; 2) ассоциативность (А+В)+С=А+(В+С), (АхВ)хС=Ах(ВхС);

3)дистрибутивность умножения относительно сложения (А+В)хС=АхС+ВхС.

Доказательства свойств 1-3 следуют из определений действий на основе теории множеств.

4) Пусть U – достоверное событие, V – невозможное событие. Тогда А+ = U, Ах = V, А+V =А , АхV = V, А+U = U, АхU =А.

5) =А – закон двойного отрицания;

6) = х , = + - законы де Моргана.

 

2. Вероятность – одно из основных понятий теории вероятности. Существует несколько определений этого понятия. Классическое определение вероятности события основано на рассмотрении полной группы несовместных и равновозможных элементарных событий.

Пусть это будет полная группа событий А₁, А₂…А_n. Событию А пусть благоприятствуют m элементарных исходов.

Вероятностью события А называется отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу Р(А)=m/n, где m≤n.

Например: Пусть в урне 6 одинаковых шаров – 3 синих, 2 красных, 1 белый. Тогда полная группа событий состоит из 6 равновозможных случаев: А₁, А₂, А₃ – появится синий шар, А₄, А₅ – красный шар, А₆ – белый шар. Событию А – «появился цветной шар» - благоприятствует 5 элементарных исходов. Тогда Р(А)=5/6 – вероятность достать цветной шар. Р( )=1/6 – вероятность достать белый шар.

Из определения следует, что

1.вероятность элементарных исходов равна Р(А₁)=Р(А₂)=…=Р(А_n)=1/n.

Т.е. равновозможные события имеют одинаковую вероятность;

2. Р(А) – безразмерная величина.

Свойства вероятности:

1. Вероятность достоверного события равна 1.

Действительно, если событие U – достоверно, то любой элементарный исход благоприятствует ему, т.е.m=n. Р(U)=n/n=1.

2. Вероятность невозможного события =0.

Т.к.V – невозможное событие, то ему благоприятствует 0 событий, т.е. Р(V)=0/n=0.

3. Вероятность случайного события – положительное число, заключенное между 0 и 1. 0 < Р(А) < 1.

Т.к. 0<m<n , то 0/n<m/n<n/n, следует 0<m/n<1.

Из свойств (1-3) следует, что вероятность любого события 0≤Р(А)≤1.

Пример: 1.Набирая номер телефона, абонент забыл 2 последние цифры, и, помня, что они разные, набрал их наудачу. Найти вероятность, того, что набранные цифры окажутся нужными.

Решение: событие В – «набрать две нужные цифры». Всевозможных вариантов набора 2-х различных цифр =10х9=90, тогда Р(В)=1/90.

Пример 2. Брошены 2 кубика. Найти вероятность того, что сумма выпавших очков равна 4 (это событие А).

Неверное решение: пусть событие В – сумма не равна 4, тогда в опыте два исхода, т.е. Р(А)=1/2. Но эти события не равновозможные и не элементарные, а, значит, не образуют полную группу.

Верное решение: всевозможных исходов 6х6=36. Событию А благоприятствуют три исхода – на кубиках может быть очков 1 и 3, 3 и 1, 2 и 2, т.е. Р(А)=3/36=1/12.

 

Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же часто встречаются испытания, число возможных исходов которых бесконечно.

Например, событие А – время решения задачи меньше заданного числа.

Это один из недостатков классического определения. Второй – очень трудно иногда указать основания, позволяющие считать элементарные события равновозможными (см. пример выше).

Существует другой способ нахождения вероятности случайного события – оценка при помощи опыта. Допустим, что начальные условия, при которых может происходить данное событие, могут повторяться многократно. Говорят, что проводятся повторные испытания. Если при проведении n испытаний событие А осуществилось m раз, то

Относительной частотой события А называется отношение числа испытаний, в которых событие появилось, к общему числу фактически проведенных испытаний w(А)=m/n.

Исходя из определения, видно, что если классическую вероятность вычисляют до опыта, то относительную частоту – после опыта.

Например, отдел контроля обнаружил 7 нестандартных деталей в партии из 80 случайно отобранных. Тогда относительная частота появления нестандартных деталей w (А)=7/80.

Длительное наблюдения показали, что если опыты проводятся в одинаковых условиях, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости:

в различных опытах относительная частота изменяется мало (если

число испытаний велико) и колеблется около некоторого постоянного числа (которое принимается за приближенное значение вероятности).

Например.1.Относительная частота рождаемости девочек в различные периоды 0,486; 0,489; 0,490; 0,478;…Р(А)≈0,482.

2.Подбрасывание монеты при n=12 000 w (А)=0,5016, при n=24 000 w (А)=0,5005.

3. При стрельбе при больших n w (А) – вероятность попадания стрелка.

Статистическое определение. Вероятностью событияА называется число, около которого группируются относительные частоты этого события, т.е. это предел, к которому стремиться относительная частота при неограниченном увеличении числа испытаний. Р(А)= .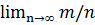

Легко проверить, что все свойства вероятности классического определения сохраняются и здесь.

Недостатком этого определения является неоднозначность статистической вероятности, ее приблизительность (0,4; 0,39; 0,41…).

 

3.Пусть А и В – два несовместных события одного и того же испытания.

Теорема. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий Р(А+В)=Р(А)+Р(В).

Док-во. Пусть общее число равновозможных несовместных исходов испытания равно n, причем m₁ из них благоприятствуют событию А, а m₂ – событию В. Т.к. А и В несовместны, то событию А+В благоприятствуют (m₁+m₂) исхода, Тогда по классическому определению вероятности Р(А+В)= (m₁+m₂)/n= m₁/n+m₂/n=Р(А)+Р(В).

Следствия.1.Если события А, В, С,… - попарно несовместны, то Р(А+В+С+…)=Р(А)+Р(В)+Р(С)+….

2.Если А и В совместны , то Р(А+В)= Р(А)+Р(В)-Р(АхВ)

Док-во. Т. к. событию (А+В) благоприятствуют (m₁+m₂-m₃) исхода по теории множеств, где m₃ - количество одновременных событий. Тогда Р(А+В)= (m₁+m₂-m₃)/ n= m₁/ n+ m₂/ n- m₃/ n=Р(А)+Р(В)-Р(АхВ).

3.Сумма вероятностей n несовместных событий, составляющих полную группу, равна 1, Р(А₁)+Р(А₂)+…Р(А_n)=1.

Док-во. Р(А₁+А₂+…+А_n)=Р(U)=1.

4.Сумма вероятностей противоположных событий равна 1, Р(А)+Р(А)=1. (доказывается аналогично)

 

Например. Завод получает сырье только из одного города А, В или С. Вероятность получения из А равна 0,7; из В – 0,2. Какова вероятность того, что очередная партия груза будет получена из С?

Решение: Р=1-(0,7+0,2)=0,1.

 

Несколько событий могут находиться между собой в таких взаимоотношениях, что вероятность наступления какого-либо из событий зависит от того, произошло или не произошло другое событие.

Вероятность события А, вычисленная при условии, что произошло событие В, называется условной и обозначается Р(А\В). События А и В при этом называются зависимыми, и Р(А\В)≠Р(А).

 

Если же вероятность события А не зависит от наступления события В, то такую вероятность называют безусловнойР(А), а события А и В –независимыми, Р(А/В)=Р(А).

Например. В урне 3 белых и 3 черных шара. Из нее последовательно вынимают 2 шара. Найти вероятность появления белого шара (событие А) при втором испытании.

Решение. Два случая:1) Если в 1 раз вынули белый шар (событие В), то останется 5 всего, их них 2 белых. Тогда Р(А/В)=2\5.

2) Если в 1 раз – черный, то Р(А/ )=3\5.

 

Теорема. Вероятность произведения двух событий А и В (их совместного появления) равна произведению вероятностей одного из них на условную вероятность другого, при условии, что произошло первое. Р(АхВ)=Р(А)хР(В/А)=Р(В)хР(А/В).

Док-во. Пусть общее число равновозможных исходов равно n.Причем событию А благоприятствует m₁ исход, событию В - m₂ исхода, событию АхВ - m₃ исхода. Т.к. событие А произошло, то равновозможных исходов m₁, для В из них благоприятствуют m₃ исхода, тогда Р(В/А)=m₃/m₁= (m₃/n)/( m₁/n)= Р(АхВ)/Р(А), т.е. Р(АВ)=Р(А)Р(В/А). (аналогично доказывается и другая часть формулы)

 

Следствия:1. Если А, В, С некоторые события, то Р(АВС)=Р(А)Р(В/А)Р(С/АВ)

2. Если А и В – независимы, т.е. Р(А/В)=Р(А), то Р(АхВ)=Р(А)Р(В).

3. Если А, В, С… независимы, то Р(АВС…)=Р(А)Р(В)Р(С)…

4. Если события А, В, С – независимы, то вероятность того, что произойдет хотя бы одно из них равна Р(А+В+С)=1 – Р )Р( )Р( ).

 

Пример. 1.Из полной колоды карт (52штуки) вынимают наугад 3 карты. Найти вероятность того, что среди них не окажется ни одного туза. Решение: события А, В, С – «1, 2, 3-я карта не туз» .

Р(АВС)=Р(А)Р(В/А)Р(С/АВ)=48/52 х 47/51 х 46/50=0,783.

Пример. 2. Вероятность попадания в цель при стрельбе из 2-х орудий равна соответственно 0,7 и 0,8. Найти вероятность попадания при одном залпе из 2-х орудий хотя бы одним из них.

Решение. 1 способ: событие А – попадание первого орудия, В – второго. События А и В – независимы, тогда

Р(А+В)=Р(А)+Р(В)-Р(АВ)=0,7+0,8-0,7х0,8=0,94.

2 способ. Р(А+В)=1-q₁q₂=1-0,3х0,2=0,94, где q₁ и q₂ – вероятности противоположных событий и .

 

4. Во многих реальных ситуациях событие А может наступить при условии появления одного из несовместных событий Н₁, Н₂,…Н_n, которые образуют полную группу. Т.к заранее неизвестно, какое из Н_i наступит, то их называют гипотезами.

Пусть известны вероятности гипотез Р(Н_i) и условные вероятности события А при каждой из этих гипотез, т.е. Р(А/Н_i). Необходимо определить безусловную вероятность Р(А), которая бы учитывала все случаи появления события А.

Т.к. А появляется тогда и тогда, когда осуществляется одно из несовместных событий АН₁, АН₂,…АН_n, т.е А=АН₁+АН₂ +…+АН_n. Тогда по теореме сложения

Р(А)=Р(АН₁)+Р(АН₂)+…+Р(АН_n)=Р(Н₁)Р(А/Н₁)+…+Р(Н_n)Р(А/Н_n)

Р(А)=∑Р(Нi)Р(А/Нi)– формула полной вероятности:

вероятность события А, которое может наступить при условии появления одного из несовместных событий Н₁, Н₂… Н_n , равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А.

Пример. В 3-х ящиках разложены детали:

в 1 ящике – 100 дет., нестандартных из них 4;

во 2 ящ. – 120 дет., нестандартных 6;

в 3 ящ. - 80 дет., нестан. 8.

Из одного (взятого произвольно) ящика вынимается 1 деталь. Чему равна вероятность того, что деталь окажется нестандартной (событие A)?

Решение: гипотезы Н₁ – деталь взята из 1 ящика, Н₂ - из 2 ящика, Н₃ - из 3 ящика. Все они равновозможные, Р(Н₁)=Р(Н₂)=Р(Н₃)=1/3.

Условные вероятности А при условии, что произошло Н_i равны Р(А/Н₁)=4/100, Р(А/Н₂)=6/120, Р(А/Н₃)=8/80 .

Р(А)=1/3 х 4/100 + 1/3 х 6/120 + 1/3 х 8/80 = 18/300.

 

Если же испытание произведено, и в результате него появилось событие А и известны Р(А/Н_к), то возникает вопрос: с какой из гипотез Н₁,… Н_n следует связывать появление событие А, т.е. с какой вероятностью можно утверждать , что событие А произошло при наступлении события Н_i.

Рассмотрим Р(АН_к)=Р(А)Р(Н_к/А)=Р(Н_к)Р(А/Н_к) .

Р(Н_к/А)=Р(Н_к)Р(А/Н_к)/Р(А) , т.к. Р(А)= ∑Р(Н_i)Р(А/Н_i), то

 

Р(Н_к\А)= .

Полученные формулы называются формулами Байеса (опубликованы в 1764 г.). Они позволяют переоценить вероятности гипотез после того, как испытание произведено, т.е. становится известным результат опыта, в итоге которого появилось событие А.

Пример. Источниками загрязнения реки являются 2 предприятия, причем известно, что вероятность того, что сброс производен 1-м предприятием – в 90% случаев, 2 предприятием - в 10%. Известно, что в 15% стока 1 предприятия, а в 92% второго ртуть превышает предельно допустимую концентрацию. Определить какому предприятию может принадлежать обнаружившийся сброс, если взятая проба превышает норму по ртути.

Решение. Событие А – превышена норма ртути. событие Н₁ – сброс 1-м предприятием, событие Н₂ - сброс 2-м предприятием. Тогда Р(А/Н₁)=0,15, Р(А/Н₂)=0,92, Р(Н₁)=0,9, Р(Н₂)=0,1.

Р(Н₁/А)=0,15 х 0,9 / (0,15х0,9+0,92х0,1)=0,595

Р(Н₂/А)=0,92х0,1/(0,15х0,9+0,92х0,1)=0,405.

С большей вероятностью можно сказать, что сбросы принадлежат 1-му предприятию.

 

5. Случайной называется величина(будем обозначать СВ), которая в результате испытания принимает то или иное значение, которое зависит от случайных обстоятельств данного испытания и заранее не может быть предсказано.

Например: число очков при бросании кубика, время решения задачи, уровень тревожности у ученика.

Случайные величины обозначаются Х, У, Z…, а их возможные значения х, у, z… Они могут принимать как конечное число значений, так и бесконечное.

Дискретной (прерывной) называют случайную величину, которая принимает конечное (или счетное) множество возможных значений.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого промежутка (их число, очевидно бесконечно).

Однако характер дискретной случайной величины перечислением возможных значений не определяется. Необходимо еще знать, насколько часто будут осуществляться одни значения и насколько редко – другие.

Законом распределения ДСВ называется соответствие между возможными значениями СВ и их вероятностями (просто распределением): х_i →р_i .

Способы задания закона распределения:

1. Табличный

Х	х1	х2	…	хn
Р	р1	р2	…	рn

 

2. Аналитический (в виде формул) р_i=f(х_i) или Р(Х= х_к)= р_к, к= .

3. Графический. Для этого в прямоугольной декартовой системе координат строят точки (х_к , р_к) и соединяют их последовательно отрезками. Полученная ломаная линия называется многоугольником распределения случайной величины Х.

 

Р

р₄

р₂

р₁

0 х₁ х₂ х₃ х₄ х_к Х

Рис. 4.

Т.к. в одном испытании случайная величина принимает одно и только одно значение, то следует, что события Х= х₁, Х= х₂, … образуют полную группу событий, т.е. р_к=1 – условие нормировки.

Универсальной характеристикой, одинаково пригодной как для дискретной случайной величины, так и для непрерывной, является функция распределения случайной величины.

Функцией распределенияназывается функция F(х), равная вероятности того, что случайная величина принимает значение меньшее, чем заданное х, т.е. F(х)=Р(Х<х).

Для ДСВ: F(х)=∑р_к, (х_к <х) – по теореме сложения

Тогда вероятность того, что СВ Х примет значения из [а, в)

Р(а≤х<в)=Р(Х<в)-Р(Х<а)=F(в)- F(а).

 

Пример. Х – число очков, выпавших при бросании кубика. Тогда закон распределения

Х
Р	1\6	1\6	1\6	1\6	1\6	1\6

 

F(3)= Р(Х<3)= р₁+р₂=2\6,

 

Построим функцию распределения

0, при х≤1 F(X)

1/6, при 1<х≤2 1

2/6, при 2<х≤3

F(X) = 3/6, при 3<х≤4

4/6, при 4<х≤5

5/6, при 5<х≤6

1, при х>6 0 1 2 3 4 5 6 Х

Рис.5.

 

Функция распределения обладает следующими свойствами:

1. Все значения F(х) принадлежат[0; 1], т.е. 0≤F(х)≤1 (следует из определения и свойств вероятности)

2. Функция F(х) неубывающая, т.е. если х₂ ≥ х₁, то F(х) ≥F(х) (по свойствам сумм)

3. Если все возможные значения ДСВ и НСВ принадлежат [а, в], то при х≤а F(х)=0, при х>в F(х)=1.

 

6. Хотя полное описание СВ дается законами распределения, но часто они бывают неизвестны. Тогда выгодно пользоваться числами – числовыми характеристиками СВ.

Математическим ожиданием ДСВ называют сумму произведений всех ее возможных значений на их вероятности. Обозначается М(Х), m_х, а.

Пусть СВ Х принимает значения х₁, х₂,…х_n, вероятности которых соответственно равны р₁, р₂,…р_n. Тогда

М(Х)= х₁ р₁+ х₂ р₂+…+ х_n р_n=∑ х_i р_i, причем ∑ р_i=1.

Вывод 1. Из определения следует, что М(Х) – не случайная величина, а постоянная.

 

Пример.1). Пусть СВ имеет закон распределения

 

Х
Р	0,1	0,6	0,3

М(Х)=3х0,1+5х0,6+2х0,3=3,9

Вывод2. Математическое ожидание может не совпадать ни с одним из ее возможных значений.

 

Пример. 2) Найти математическое ожидание М(Х) числа появлений события А в одном испытании, если вероятность Р(А)=р.

 

Х
Р	q	р

М(Х)=0хq+1хр=р

 

Вывод3. Математическое ожидание числа появлений событий в одном испытании равно вероятности этого события .

 

Пусть произведено n испытаний, в которых СВ Х приняла m₁ раз значение х₁, m₂ - х₂ ,…m_k раз – х_к, причем m₁+ m₂+…+ m_k=n. Найдем среднеарифметическое всех значений

= =х₁ +х₂ +…+х_k

Т.к. =w_i - относительные частоты значений х_i, то при достаточно большом n по статистическому определению вероятности

х₁р₁+х₂р₂ +…+х_kр_k , т.е. М(Х)

 

Тогда вероятностный смыслматематического ожидания случайной величины Х заключается в том, что оно приблизительно равно (при n большом) среднему арифметическому всех ее возможных значений.

Поэтому М(Х) называют средним значением, иногда центром распределения (термин «математическое ожидание» связан с азартными играми, когда игрока интересовало среднее значение ожидаемого выигрыша).

 

Свойства математического ожидания:

1. а≤М(Х)≤в, где а и в – наименьшее и наибольшее значения Х.

2. Математическое ожидание постоянной величины равно самой

постоянной.

Док-во. Х принимает одно значение С с вероятностью р=1

М(Х)=Сх1=С.

3. Постоянный множитель можно выносить за знак математического

ожидания

М(СХ)=СМ(Х)

Док-во. Пусть СВ Х задана распределением

Х	х1	х2	…	хk
Р	р1	р2	…	рk

 

Тогда СХ

СХ	Сх1	Сх2	…	Схk
Р	р1	р2	…	рk

 

М(СХ)= Сх₁р₁+Сх₂р₂ +…+Сх_nр_n=С(х₁р₁+х₂р₂ +…+х_nр_n)=СМ(Х).

 

Две СВ называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Произведением 2-х независимых СВ Х и У называется случайная величина ХУ, возможные значения которой равны произведениям каждого значения Х на каждое возможное значение У, а вероятности возможных значений ХУ равны произведениям вероятностей соответствующих множителям : р_ij →р(х_iу_j).

Суммой СВ Х и У – случайная величина (Х+У), возможные значения которой равны суммам каждого значения Х с каждым значением У, вероятности возможных значений Х+У равны произведениям вероятностей слагаемых (если Х и У – независимы) и произведениям вероятности одного слагаемого на условную вероятность другого (если они зависимы).

4. Математическое ожидание произведения 2-х независимых СВ равно произведению их математических ожиданий: М(ХУ)=М(Х)М(У)

(аналогично для n независимых СВ)

5. Математическое ожидание суммы (разности) 2-х СВ равно сумме (разности) их математических ожиданий: М(Х+У)=М(Х)+М(У)

 

Пример. Найти мат.ожидание суммы числа очков, которые могут выпасть при бросании 2 игральных кубиков.

Х – число очков на 1 кубике, У – на 2-ом.

Х
Р	1/6	1/6	1/6	1/6	1/6	1/6

Для У аналогично. Тогда распределение Х+У

Х+У
Р	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

Р₁= 1/6 х 1/6

Р₂=11/6 х 1/6+1\6х1\6= 2/36 и т.д. Причем ∑рi=1.

М(Х)=М(У)=3,5

М(Х+У)=7

Как говорилось, математическое ожидание СВ характеризует положение центра распределения. Но легко указать такие СВ, которые могут иметь одинаковые математические ожидания, но различные возможные значения. Например:

Х	-1
Р	0,5	0,5

У	-100
Р	0,5	0,5

 

М(Х)=М(У)=0 , т.е. знание лишь М(Х) не дает полные знания о СВ.

Второй числовой характеристикой СВ является дисперсия, которая характеризует степень разброса значений этой величины относительно центра распределения – математического ожидания.

Отклонением СВ Х от ее математического ожидания называют разность Х- М(Х).

Пусть СВ Х задана распределением

Х	х1	х2	…	хk
Р	р1	р2	…	рk

 

 

Тогда

 

Х-М(Х)	х1-М(Х)	х2-М(Х)	…	хk-М(Х)
Р	р1	р2	…	рk

 

 

Свойство. Математическое ожидание отклонения равно 0 (т.е. среднеарифметическое отклонений равно 0).

М(Х-М(Х))=0.

Док-во: М(Х-М(Х))= Σ(х_i-М(Х))р_i= Σ(х_i р_i - М(Х)р_i)= Σх_iр_i- ΣМ(Х)р_i=

= М(Х) - М(Х)Σр_i=0, т.к. Σр_i=1.

Дисперсией (рассеянием) СВназывают числовую характеристику, равную математическому ожиданию квадрата отклонения СВ от ее математического ожидания. D(Х)=М((Х-М(Х))²)

 

Для дискретной СВ D(Х)=∑(х_к-М(Х))²р_к, к= .

Для вычисления дисперсии часто пользуются следующей формулой:

D(Х)=М(Х²)- (М(Х))²

Вывод: D(Х)=М(Х-М(Х))²)=М(Х²-2ХМ(Х)+М(Х)²)=

=М(Х²)-2М(Х)М(Х)+(М(Х))²=М(Х²)-2М²(Х)+М²(Х)=

=М(Х²)-М²(Х) ч.т.д.