Тема 2.1. Нормальное распределение (4 ч)

 

П Л А Н

 

1. Понятие нормального распределения. Историческая справка

2. Стандартизация и нормализация данных

3. Проверка нормальности распределения

4. Разработка тестовых шкал

5. Функция Лапласа и ее использование. Правило 3σ.

 

 

1. Нормальный закон распределения играет важнейшую роль в применении статистических методов в психологии. Он лежит в основе измерений, разработки тестовых шкал, методов проверки гипотез.

Нормальное распределение подчиняется закону, который был открыт в разное время учеными Муавром (в 1733 г.), Гауссом (в 1809 г.) и Лапласом (в 1812 г.)

Де Муавр пытался решить следующую задачу: предположим, что подбрасывается симметричная монета 10 раз. Какова вероятность того, что в результате подбрасываний “орел” может выпасть 0 раз, 1 раз, …, 10 раз? Вероятности можно вычислить (по формуле Бернулли), но вычисления для большого количества подбрасываний становятся достаточно трудными. Задача, которую ставил перед собой де Муавр, состояла в том, чтобы найти уравнение кривой, которая бы хорошо аппроксимировала кривую, полученную соединением концов отрезков на графике распределения вероятностей получения определенного числа “орлов” при 10 подбрасываниях монеты:

 

 

 

Рис. 1.

 

Если бы такую кривую удалось бы найти, то проблемы вычисления вероятностей можно было бы замениять простым считыванием точек с кривых или просмотром чисел в математической таблице. Ему удалось показать, что уравнение кривой, проходящей совсем близко от кривой, соединяющей концы точек на графике (рис.1) имеет следующую формулу:

f(x)= ,(*)

где π=3,14, е=2,718 – постоянные величины. Эта формула и соответствующая ей кривая впоследствии получили название нормального распределения.

История применения закона нормального распределения в социальных и биологических науках начинается с работы бельгийского ученого А.Кетле «опыт социальной физики» (1835г.). В ней он доказывал, что такие явления, как продолжительность жизни, рост человека, возраст вступления в брак и появления первого ребенка и т.д., подчиняется строгой закономерности, которую он назвал «законом уклонения от средней величины». Ф.Гальтон, двоюродный брат Ч.Дарвина, проявление нормального закона рассматривал в связи с биологической изменчивостью, наследственностью и отбором. В дальнейшем он и его последователи доказали, что психологические особенности, например способности, также подчиняются нормальному закону. Поэтому дальнейшее развитие измерительного подхода в психологии и статистического аппарата проверки гипотез происходило на базе этого общего закона.

Т.е., начиная со второй половины XIX века измерительные и вычислительные методы в психологии разрабатываются на основе следующего принципа: если индивидуальная изменчивость некоторого свойства есть следствие действия множества причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения. Это и есть закон нормального распределения.

 

2.Каждому биологическому (в т.ч. и психологическому) свойству соответствует свое распределение в генеральной совокупности. Чаще всего оно является нормальным.

График уравнения (*) – симметричная, колоколообразнаякривая, которую называют нормальной кривой с параметрами М и σ, которые отличают друг от друга бесконечное множество нормальных кривых. Величина М соответствует среднему распределения частот генеральной совокупности (математическому ожиданию) и задает пололжение кривой на числовой оси, а σ – стандартному отклонению этого распределения и задает ширину этой кривой.

 

f 1

2 3 σ₁=σ₃, σ₁<σ₂

 

₁= _{2 3} X

Рис. 2.

Если М=0, σ=1, то такое нормальное распределение называется нормированным (стандартным, единичным нормальным), т.е.

f(x)=

Все многообразие нормальных распределений может быть сведено к одной кривой, если применить стандартизацию данных ко всем возможным измерениям свойств. Стандартизация – это процедура унификации, т.е. приведение к единым нормативам.

Стандартизация или z-преобразование данных –это перевод измерений в стандартную Z-шкалу со средним М_z=0и σ_z=1. Сначала для переменной, измеренной на выборке, вычисляется и стандартное отклонение σ_х. Затем все значения переменной x_i пересчитываются по формуле: z_i= . Величина z= называется единичным стандартным отклонением.

В результате преобразованные значения (z-значения) непосредственно выражаются в единицах стандартного отклонения от среднего. Если для одной выборки несколько признаков переведены в z-значения, появляется возможность сравнения уровня выраженности разных признаков у того или иного испытуемого. Для того, чтобы избавиться от неизбежных отрицательных и дробных значений, можно перейти к любой другой известной шкале: IQ ( σ=15), Т-оценок ( σ=10), 10-бальной стенов - ( σ=2) и др. Перевод в новую шкалу ос уществляется путем умножения каждого z-значения на заданную σ и прибавления среднего:

s_i= σ_sz_i + 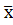_s.

При стандартизации каждое свойство будет иметь среднее 0 и стандартное отклонение 1, т.е. будет являться единичным нормальным распределением, которое используется как стандарт (эталон).

Свойства стандартного распределения:

1. Единицей измерения является стандартное отклонение.

2. Кривая приближается к оси Z по краям асимптотически – никогда не пересекая ее.

3. Кривая симметрична относительно М=Z=0. Ее Е_k=А_s=0, т.к. она симметрична и средневершинна.

4. Кривая имеет характерный изгиб: точка перегиба лежит точно на расстоянии в одну σ от М.

5. Площадь между кривой и осью Z равна 1.

f

 

 

 

 

 

-3 -2 -1 0 1 2 3 Z

68,26%

 

95,44%

 

99,73%

 

Рис. 3.

Вершина нормированной кривой f≈0,3989.

Пятое свойство объясняет название единичное нормальное распределение, благодаря нему площадь под кривой интерпретируется как вероятность, или относительная частота. Действительно, вся площадь под кривой соответствует вероятности того, что признак примет любое значение из всего диапазона его изменчивости (от - ∞ до +∞).

Нормированная кривая позволяет увидеть общее свойство любых кривых нормального распределения – это то, что они имеют одинаковую долю площади под кривой между одними и теми же двумя значениями признака, выраженными в единицах стандартного отклонения, а именно:

1. ≈68% площади под кривой находится в пределах одной σ от среднего, т.е. М ;

2. ≈95% площади под кривой находится в пределах двух σ от среднего, т.е. М ;

3. ≈99,73% площади под кривой находится в пределах трех σ от среднего, т.е. М .

f

 

 

68,26%

95,44%

99,73%

М-3σ М-2σ М-σ М М+σ М+2σ М+3σ Z

Рис. 4.

Для единичного нормального распределения значение Х указывает, что точка отстоит от среднего на Х единиц. Зная свойства единичного нормального распределения, можем ответить на вопросы: какая доля генеральной совокупности имеет выраженность свойства, например, от –σ до +σ; или какова вероятность того, что случайно выбранный представитель ген. совокупности будет иметь выраженность свойства, на 3σ превышающую среднее значение и т.д. В первом случае – это 68%, а во втором – (100 – 99,72)/2=0,14%. (См. график)

Существует специальная таблица, позволяющая определить площадь под кривой справа от любого положительного значения z. Пользуясь ею, можно определить вероятность встречаемости значений признака из любого диапазона. Это широко используется при интерпретации данных тестирования.

 

Пример 1. Значение IQ по шкале Векслера (М=100, σ=15) некоторого испытуемого равнно 125. Вопрос: как часто встречаются значения IQ выше 125?

Перейдем от шкалы IQ к единицам стандартного отклонения:

z=(125 – 100)/15=1,66.

По таблице находим площадь под кривой справа от этого значения, она равна 0,0485. Это значит, что IQ 125 и выше встречается редко – менее, чем в 5% случаев.

 

Пример 2. Какова вероятность того, что случайно выбранный человек будет иметь IQ по шкале Векслера в интервале от 100 до 120.

В единицах стандартного отклонения z₁=0 и z₂=1,33. Площадь справа от z₁ равна 0,5 и справа от z₂ - 0,918, тогда площадь между z₁ и z₂ равна 0,918– 0,5 = 0,4082. Т.е. вероятность того, что случайно выбранный человек будет иметь IQ по шкале Векслера в интервале от 100 до 120, равна 0, 41.

 

Иногда складывается неправильное мнение, что существует обязательная связь между нормальным распределением – идеальным описанием некоторых распределений частот – и практически любыми данными. Нормальная кривая – это изобретение математика, довольно хорошо описывающее полигон частот измерений нескольких различных переменных. Никогда не была (и не будет) получена совокупность данных, которые бы были точно нормально распределены. Но иногда полезно утверждать, допуская незначительную ошибку, что рассматриваемая переменная распределена нормально. Существует множество методов, позволяющих анализировать данные без всякого предположения о виде распределения, как выборки, так и генеральной совокупности. Но есть три важных аспекта применения нормального распределения:

1. Проверка нормальности выборочного распределения для принятия решения о том, в какой шкале измерен признак – в метрической или порядковой.

2. Разработка тестовых шкал.

3. Статистическая проверка гипотез, в том числе – при определении риска принятия неверного решения.

 

 

3. Для проверки нормальности используют различные процедуры, позволяющие выяснить отличается ли выборочное распределение измеренной величины от нормального или нет. Необходимость такого сопоставления возникает, когда мы сомневаемся, в какой шкале представлен признак, что очень важно для выбора методов анализа данных. Если исследователь принимает решение ранжировать данные, принимая их измеренными в порядковой шкале, то он может потерять часть исходной информации о различиях между испытуемыми, о взаимосвязях между признаками и т.д. Кроме того, метрические данные позволяют использовать значительно широкий набор методов анализа.

Как следствие закона нормального распределения можно рассматривать следующий вывод:

Если выборочное распределение не отличается от нормального, то это значит, что измеряемое свойство измерено в метрической шкале (чаще всего в интервальной).

Общей причиной отклонения формы выборочного распределения признака от нормального чаще всего является особенность процедуры измерения: используемая шкала может обладать неравномерной чувствительностью к измеряемому свойству в разных частях диапазона его изменчивости. Например, при измерении некоторого признака при решении задач за определенное время, если задачи простые, то большая часть испытуемых, решит все или почти все задания, и такая процедура измерения будет чувствительна только к тем, кому они достаточно трудны. В итоге получим распределение с правосторонней асимметрией.

Другой причиной отклонения от нормальности может являться наличие экстремальных значений. Такими можно считать значения признака, отличающиеся от среднего более чем на 2σ (при 50) и более чем на 3σ (при Если таких значений не много, то можно исключить из выборки.

 

Существует несколько способов проверки нормальности, рассмотрим некоторые из них.

Графический способ.Строят либо квантильные графики, либо графики накопленных частот. Квантильные графики строятся следующим образом. Сначала определяются эмпирические значения признака, соответствующие 5,10, …, 95-процентилю. Затем по таблице для каждого их них находятся z-значения (теоретические). Эти два ряда чисел задают координаты точек на графике: эмпирические значения откладываются на оси ОХ, а соответствующие им теоретические – на оси ОУ. Для нормального распределения все точки должны лежать на одной прямой или рядом с ней. Чем ближе точки расположены к прямой, тем больше распределение соответствует нормальному.

Аналогично строятся графики накопленных частот. При этом на оси ОХ через равные интервалы откладываются значения накопленных частот, например 0,05; 0,1;…0,95. Затем определяются эмпирические значения, соответствующие каждому значению накопленной частоты, которые переводятся в z-значения. По таблице определяются накопленные частоты для каждого z-значения, которые и откладываются на оси ОУ. Если точки лежат почти на одной прямой, то данное распределение соответствует нормальному.

 

Критерии асимметрии и эксцесса. Эти критерии определяют допустимую степень отклонения эмпирических значений асимметрии и эксцесса от нулевых значений, соответствующих нормальному распределению. Величина допустимых отклонений определяется так называемыми стандартными ошибками асимметрии и эксцесса. Для асимметрии и эксцесса стандартные ошибки определяются по формулам: А_ssd=3 , Е_{k sd} =5 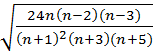, где – объем выборки.

Выборочные значения асимметрии и эксцесса не отличаются от нуля, если они не превышают по абсолютной величине значения своих стандартных ошибок. Это и будет признаком соответствия выборочного распределения нормальному закону.

Статистический критерий нормальности Колмагорова-Смирнова. Данный критерий позволяет оценить вероятность того, что данная выборка принадлежит генеральной совокупности с нормальным распределением. Если эта вероятность р≤0,05, о данное эмпирическое распределение существенно отличается от нормального, а если р>0,05, то делают вывод о приблизительном соответствии данного эмпирического распределения нормальному.

 

4. Тестовые шкалы разрабатываются для того, чтобы оценить индивидуальный результат тестирования путем сопоставления его с тестовыми нормами, полученными на выборке стандартизации. Выборка стандартизации специально формируется для разработки тестовой шкалы – она должна быть репрезентативна генеральной совокупности, для которой планируется применять данный тест. Впоследствии будем считать, что и испытуемый, и выборка стандартизации принадлежат одной и той же генеральной совокупности.

Исходным принципом при разработке тестовой шкалы является предположение о том, что измеряемое свойство распределено в генеральной совокупности по нормальному закону. Поэтому измерение в тестовой шкале данного свойства на выборке стандартизации должно обеспечивать нормальное распределение, а значит, тестовая шкала будет являться интервальной. Если же это не так, то свойство удалось отразить в шкале порядка. Т.е., основная проблема стандартизации теста заключается в разработке такой шкалы, в которой распределение тестовых показателей на выборке стандартизации соответствовало бы нормальному распределению.

Исходные тестовые оценки – это количество ответов на вопросы тестов, время или количество решенных задач и т.д. Это первичные, «сырые» оценки. Итогом стандартизации являются тестовые нормы – таблицы пересчета «сырых» оценок в стандартные тестовые шкалы.

Существует множество стандартных тестовых шкал: z –шкала, стены, процентили, шкала Векслера (IQ) и др. Общим для них является соответствие нормальному распределению, а различаются они только средним значением и стандартным отклонением (который выступает, как масштаб, определяющий дробность шкалы).

 

 

 

 

 

 

 

-4σ -3σ -2σ -σ М +σ +2σ +3σ

Тестовый показатель

 

z-шкала

-4 -3 -2 -1 0 1 2 3

 

Стены

1 2 3 4 5 6 7 8 9 10

 

Процентили

 

1 5 10 20 30 40 50 60708090 95 99

Шкала Векслера

(IQ) 55 70 85 100 115 130 145

Стенайны

 

Рис. 5.

Общая последовательность стандартизации (разработки тестовых норм – таблицы пересчета «сырых» данных в стандартные тестовые) состоит в следующем:

1) определяется генеральная совокупность, для которой разрабатывается методика и формируется репрезентативная выборка стандартизации;

2) по результатам применения первичного варианта теста строится распределение «сырых» баллов;

3) проверяют соответствие полученного распределения нормальному закону;

4) если распределение «сырых» баллов соответствует нормальному, производится линейная стандартизация;

5) если распределение «сырых» баллов не соответствует нормальному, то производят перед линейной стандартизацией эмпирическую нормализацию или проводят нелинейную нормализацию.

Линейная стандартизация заключается в том, что определяются границы интервалов «сырых» оценок, соответствующие стандартным тестовым показателям. Эти границы вычисляются путем прибавления к среднему «сырых» оценок (или вычитанием из него) долей стандартных отклонений, соответствующих тестовой шкале.

Например. Пусть получено распределение «сырых» оценок, соответствующее нормальному, со средним М_х= = 22 и σ_х=6. В качестве стандартной тестовой шкалы выбрана 10-бальная шкала стенов, предложенная Р. Кеттелом (М_st=5,5; σ_st=2). Результатом линейной стандартизации должна быть таблица пересчета из шкалы «сырых» оценок в шкалу стенов. Для этого каждому стандартному значению ставится в соответствие интервал «сырых» оценок. Границы интервала определяются следующим образом. Среднее «сырых» оценок должно делить шкалу стенов пополам (1-5 ниже среднего, 6-10 – выше среднего). Т.е. среднее «сырых» оценок М_х==22 – это граница стенов 5 и 6. Следующая граница справа – отделяющая стены 6 и 7 – отстоит от среднего на σ_st/2. Этой границе должна соответствовать граница «сырых» оценок М_х+ σ_х/2= 22+3=25. Аналогично, определяются границы оставшихся интервалов, а границы крайних интервалов остаются открытыми. Результатом являются тестовые нормы – таблица пересчета «сырых» баллов в стандартные тестовые оценки:

 

Стены
«Сырые» баллы	<11	11-13	14-16	17-19	20-22	23-25	26-28	29-31	32-34	>34

 

Пользуясь этой таблицей тестовых норм «сырой» балл переводят в шкалу стенов, что позволяет интерпретировать выраженность измеряемого свойства.

 

В общем случае границы интервалов определяются по формуле z-преобразования:

z= = x_i= M_x + ( ,

где - искомая граница интервала «сырых» баллов, граница интервала в стандартной тестовой шкале, M_x, - средние и стандартные отклонения «сырых» баллов (х) и стандартной шкалы (st).

Эмпирическая нормализация применяется, когда распределение «сырых» баллов отличается от нормального. Она заключается в изменении содержания тестовых заданий. Например, если «сырая» оценка – это количество задач, решенных испытуемыми за данное время, и получено распределение с правосторонней асимметрией, то это значит, что слишком большая доля испытуемых решает больше половины заданий. В этом случае необходимо либо добавить более трудные задания, либо сократить время решения.

Нелинейная нормализация применяется, если эмпирическая нормализация невозможна или нежелательна. Тогда перевод «сырых» оценок в стандартные производится через нахождение процентильных границ групп в исходном распределении, соответствующих процентильным границам групп в нормальном распределении стандартной шкалы. Каждому интервалу стандартной шкалы ставится в соответствие такой интервал шкалы «сырых» оценок, который содержит ту же процентную долю выборки стандартизации. Величины долей определяются по площади под единичной нормальной кривой, заключенной между соответствующими данному интервалу стандартной шкалы z-оценками.

Например, для того, чтобы определить, какой «сырой» балл должен соответствовать нижней границе стена 10, необходимо сначала выяснить, какому z-значению соответствует эта граница (z=2). Затем по таблице нормального распределения определяем, какая доля площади под кривой находится правее этого значения (0,023). После этого находим, какое значение отсекает 2,3% наибольших значений «сырых» баллов выборки стандартизации. Найденное значение и будет соответствовать границе 9 и 10 стена.

Пример. Пусть данный тест предполагает решение 20 заданий. Объем выборки стандартизации n=200 человек. Таблица распределения частот «сырых» оценок с правосторонней асимметрией:

 

балл

частота

 

В качестве стандартной возьмем шкалу стенайнов, для каждой градации которой известны процентные доли. Исходя их этих процентных долей и таблицы частот, строится таблица тестовых норм. Сначала отбираются 4% испытуемых, решивших наименьшее количество заданий. Это 8 человек, которые решили менее 4 заданий. Это число заданий будет соответствовать 1-му стенайну. Второму – результат следующих 7% (14) испытуемых: от 4 до 6 заданий и т.д. В итоге нелинейной стандартизации – таблица перевода «сырых» баллов шкальные, стенайны:

 

стенайны
%
«сырые» оценки	<4	4-6	7-9	10-12	13-14	15-16	17-18

 

 

Изложенные основы психодиагностики позволяют сформулировать математически обоснованные требования к тесту. Тестовая методика должна содержать:

· описание выборки стандартизации;

· характеристику распределения «сырых» баллов с указанием среднего и стандартного отклонения;

· наименование, характеристику стандартной шкалы;

· тестовые нормы – таблицы пересчета «сырых» баллов в шкальные.

 

5. Вспомним, нормальное распределение имеет следующую формулу

f(x)= , тогда функция распределения (из теории вероятостей) F(х)= 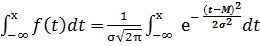, тогда функция распределения единичного нормального распределения F(х)= . Учитывая симметричность нормированного распределения, рассматривают следующую функцию

Ф(х)= ,которая называется функцией Лапласа. Очевидно, что она нечетна, т.е. Ф(-х)=-Ф(х). Значения этой функции определяются по таблице. Эта функция помогает определить вероятность встречаемости значений признака в определенном интервале (а, в).

По теории вероятностей

Р(а<Х<в)= F(в)- F(а)= , если , то получим

Р(а <Х<в)=Ф( ) - Ф( ).

Тогда вероятность того, что отклонение значений признака от своего среднего не превысит утроенного стандартного отклонения, будет равна

Р(М-3σ <Х<М+3σ)= Ф( ) - Ф( )= Ф( 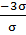) - Ф( ) = Ф( )+ Ф( ) =2Ф(3)≈2 0,4987≈0,9973.

Т.е. вероятность того, что отклонение значений признака от своего среднего превысит утроенное стандартное отклонение, очень мала 0,0027, т.е. это может произойти только в 0,27% случаев, т.е. практически невозможно. В этом заключается правило 3σ:

если признак распределен по нормальному закону, то абсолютная величина его отклонения от своего среднего не превосходит утроенного среднеквадратичного отклонения.

На практике это используется следующим образом: если распределение изучаемой величины неизвестно, но правило 3σ выполняется, то есть основание полагать, что изучаемый признак распределн нормально (в противном случае – нет).