 |
Главная |
Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсиям
|
из
5.00
|

Для примера 2.
Пусть даны две группы значений со следующими частотными распределениями:
группа 1 группа 2
| Х | ||
| n |
| Х | ||
| n |
 =
=  =
=  ,
,  =
=  ,
,
 =
=  ≈6
≈6
 =
=  ≈3,84
≈3,84
 =
=  4,56
4,56
 =
=  =0,08
=0,08
 =
=  =4,64
=4,64
Или  = 4,56 + 0,08 =4,64.
= 4,56 + 0,08 =4,64.
Еще одна мер изменчивости – среднее отклонение - вычисляется легче, чем стандартное отклонение, но используется реже. Сумма всех отклонений (по 3-му свойству средней) равна нулю  =0. Но если рассматривать отклонения как расстояния от
=0. Но если рассматривать отклонения как расстояния от  , без учета знака (
, без учета знака (  , то сумма этих расстояний будет характеризовать изменчивость данных.
, то сумма этих расстояний будет характеризовать изменчивость данных.
Средним отклонением называется среднеарифметическое отклонение всех значений признака от своего среднего
md =  .
.
Среднее отклонение не часто используется как мера изменчивости, даже не смотря на легкость вычисления, т.к. на нее тоже влияют экстремальные значения, и она не имеет теоретического обоснования, как дисперсия.
Коэффициентом вариации Vназывают выраженное в процентах отношение среднего квадратического отклонения к средней:
V=σ/  .
.
Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большее рассеяние по отношению к средней, у которого коэффициент вариации больше. Коэффициент вариации – безразмерная величина, поэтому он пригоден для сравнения изменчивости данных с различной размерностью, например, данные одной выборки в см, а другой – в м.
3. Ранее были рассмотрены графики распределений, которые характеризуются асимметрией и эксцессом. Практически точно симметричные полигоны или гистограммы частот почти никогда не встречаются. Поэтому степень асимметрии – одно из наиболее важных свойств распределения частот. Легко выявить или распознать асимметрию, если рассматривать графики распределения частот, но это не всегда возможно или удобно. Поэтому изобретены различные статистики, оценивающие вид и степень асимметрии.
Показатель асимметрии кривой эмпирического распределения определяется по формуле: Аs=  . Он показывает степень отклонения графика распределения частот от симметричного вида относительно среднего значения. Чем больше отклонения от нуля, тем больше асимметрия.
. Он показывает степень отклонения графика распределения частот от симметричного вида относительно среднего значения. Чем больше отклонения от нуля, тем больше асимметрия.
Из того факта, что на величину среднего крайние (экстремальные) значения оказывают большее влияние, чем на медиану, следует ускоренный метод измерения асимметрии распределения.
В унимодальных положительно асимметричных распределениях средние больше медианы, которая в свою очередь больше моды. В отрицательно асимметричных распределениях наоборот. Это значит, что положение среднего по отношению к медиане информирует нас в какой-то степени об асимметрии распределения. Это верно для умеренно больших выборок, например объемом 50 или более.
Простейшая мера асимметрии, основанная на этих фактах, определяется следующим образом:
Аs= 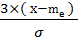
Такую меру асимметрии можно использовать для сравнения различных распределений, т.к. деление на  сделало эту меру независимой от изменчивости признака.
сделало эту меру независимой от изменчивости признака.
Итак, нами было рассмотрено, как статистики описывают три свойства или особенности выборок: центральную тенденцию, изменчивость и симметрию. Четвертое свойство завершает набор особенностей распределений, представляющих интерес при анализе данных. Иногда важно получить представление о том являются ли графики островершинными или плоскими. Эксцесс – греческое слово, обозначающее остроконечность кривой.
Показатель эксцесса– мера плосковершинности или остроконечности графика распределения измеренного признака. Он определяется формулой:
Еk= 
Островершинное распределение характеризуется положительным эксцессом, а плосковершинное – отрицательным, причем -3<Еk<0.
При нормальном распределении, как уже говорилось Аs= Еk=0.
|
из
5.00
|
Обсуждение в статье: Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсиям |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

