Среднеквадратичным отклонением СВ Х (стандартным

отклонением) называют квадратный корень из дисперсии.

σ(х) =

 

Размерность: М(Х) – такая же, что СВ Х;

D(Х) – математическое ожидание квадрата отклонения,

т.е. ед.²;

σ(х) – такая же, что СВ Х.

 

Пример.1. СВ Х задана законом распределения

Х
Р	0,1	0,4	0,5

 

М(Х)=2х0,1+3х0,4+10х0,5=6,4

D(Х)=(2-6,4)²х0,1+(3-6,4)²х0,4+(10-6,4)²х0,5=13,04

или

D(Х)=М(Х²)-М²(Х)=54-6,4²=13,04, где М(Х²)=2²х0,1+3²х0,4+10²х0,5=54

σ(х)= ≈3,61.

 

Свойства дисперсии:

1. D(Х)≥0. Дисперсия любой СВ Х –число неотрицательное

(следует из определения).

2. Дисперсия постоянной величины С равна 0.

D(С)=0

Док-во. D(С)=М((С-М(С))²)=М((С-С)²)=М(0)=0.

3. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

D(СХ)=С² D(Х)

Док-во. D(СХ)=М((СХ-М(СХ))²)=М(С²(Х-М(Х))²)=С²М((Х-М(Х))²)=С² D(Х)

4. Дисперсия суммы и разности двух независимых величин равна сумме дисперсии этих величин.

D(Х+У)= D(Х)+ D(У)

Док-во.

D(Х+У)=М((Х+У)²)-(М(Х+У))²=М(Х²+2ХУ+У²)-(М(Х)+М(У))²=М(Х²)+2М(Х)М(У)+М(У²)-(М(Х))²-2М(Х)М(У)-(М(У))²=М(Х²)-(М(Х))²+М(У²)-(М(У))²= D(Х)+ D(У).

D(Х-У)= D(Х)+ D(-У)= D(Х)+(-1)² D(У)= D(Х)+D(У).

 

Кроме математического ожидания, которое характеризует положение центра и закона распределения, рассматривают еще 2 аналогичные характеристики: медиану m_e и моду m_o .

Медиана – это такое значение m_e , которое делит S под графиком плотности вероятности пополам, т.е. это корень F(m_e)=0,5.

Мода – это значение СВ Х m_o, которое соответствует максимальному значению вероятности.

Начальным моментом порядка к СВ Х называют математическое ожидание величины Х^к - ν_к=М(Х^к), т.е. ν_к=∑х_i ²р_i .

Математическое ожидание – начальный момент 1-го порядка, М(Х²) – 2-го порядка.

Центральным моментом порядка к СВ Х называют математическое ожидание к-й степени отклонения этой величины от ее математического ожидания μ_к=М((Х-М(Х))^к)

Дисперсия – центральный момент 2-го порядка.

 

7.Применение вероятностных методов в различных областях психологии является очень широким и разносторонним. Приведем лишь несколько примеров.

Чаще всего психология имеет дело со случайными величинами. Психические явления следует считать случайными. Вариативность, случайная или закономерная изменчивость – наиболее часто встречающиеся в психологических явлениях категории. Большинство психических процессов случайны, поскольку непредсказуемо изменчивы, вариативны и многообразны из-за сочетания многочисленных внутренних и внешних причин и обстоятельств. Любая прогнозная модель в психологии прогнозирования является моделью случайного процесса как случайной функции, аргументом которой является время.

В психологии труда используется оценка времени реакции водителей. Время реакции человека является случайной величиной, которая характеризуется двумя параметрами: математическим ожиданием и дисперсией. Для того, чтобы установить факт влияния на время реакции, например, такого фактора, как утомление, нужно сравнить два условных распределения – до утомления водителя и после утомления (т.е. состояния человека отдохнувшего и уставшего).

При верификации гипотез составляются матрицы условных распределений и тех ошибок, которые совершает испытуемый. При этом используются априорные вероятности гипотез, которые апостериори уточняются с помощью формул Байеса.

В математической статистике существуют критерии, с помощью которых на основе сравнения дисперсий двух распределений можно сделать выводы об истинности или ложности психологических гипотез. Это F-критерий (или критерий Фишера-Снедекора) для сравнения двух дисперсий и G-критерий Кохрана для сравнения нескольких дисперсий.

Таким образом, теоретико-вероятностные и математико-статистические методы и модели являются неотъемлемой частью психологического исследования и психологии как науки.

1.3.2. Первичные описательные статистики(2 ч.)

 

П Л А Н

 

1. Меры центральной тенденции. Квантили распределения.

2. Меры изменчивости. Коэффициент вариации.

3. Асимметрия и эксцесс распределения.

 

Для обобщения результатов измерения используются математические модели описания, которые представляют их в доступном для интерпретации виде. К первичным описательным статистикам обычно относят числовые характеристики частотного выборочного распределения. Каждая такая характеристика отражает в одном числовом значении свойство распределения множества результатов измерения: с точки расположения их на числовой оси либо с точки зрения их изменчивости. Компактное описание при помощи первичных статистик позволяет интерпретировать результаты измерений, например, путем сравнения первичных статистик разных групп. К ним, прежде всего, относятся меры центральной тенденции и меры изменчивости.

1. Мера центральной тенденции – это число, характеризующее выборку по уровню выраженности измеренного признака. Самые распространенные из существующих мер центральной тенденции - это выборочное среднее , мода m_o и медиана m_e.

Среднее(среднее арифметическое) – сумма всех значений измеренного признака, деленная на их количество.

Если все значения признака Х в выборке объемом n различны, т.е. х₁, х₂,…х_n, то = . Если же значение х₁ встречается n₁ раз, х₂ – n₂ раза, … х_к – n_к раз, причем Σ n_i = n, тогда

 

Свойства среднего.

1.Если к каждому значению признака прибавить (или вычесть) одно и то же число С, то среднее увеличится (или уменьшится) на это число:

= + С.

2. Если каждое значение переменной умножить (или разделить) на одно и то же число С, не равное нулю, то среденее увеличится (или уменьшится) в в С раз:

= С.

3. Сумма всех отклонений от среднего равна нулю:

=0.

Доказательства этих свойств следуют из определения среднего.

 

Выделяют также понятия групповой и общей средних.

Пусть все значения количественного признака Х разбиты на несколько групп. Рассматривая каждую группу как отдельную совокупность, можно найти ее групповую среднюю,как среднеарифметическое значений признака, принадлежащих группе. Общая средняя - среднеарифметическое значений признака, принадлежащих всей совокупности.

Теорема. Общая средняя равна среднеарифметическому групповых средних, «взвешенных» по объемам групп.

Пример 1. Пусть даны две группы значений со следующими частотными распределениями:

группа 1 группа 2

Х
n

Х
n

 

Необходимо найти общую среднюю значений двух групп.

1-й способ. Составим общее частотное распределение:

Х
n

Тогда

=

2-й способ. Если же распределения по группам не даны, но известны групповые средние:

= , = ,

 

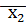То =

 

 

Мода –это такое значение признака m_o, которое имеет наибольшую частоту встречаемости. Моде (или модальному интервалу) соответствует наибольшая вершина (наибольший подъем) графика распределения частот. Если график имеет одну вершину, то такое распределение называется унимодальным. Когда наибольшая частота встречается у двух соседних значений, то мода есть среднее этих двух значений. Если распределение равномерное, то принято считать, что оно не имеет моды. Если распределение бимодальное, то в случае разных частот для вершин выделяют большую и меньшую моду.

Мода это значение признака, а не его частота!

Медиана - это такое значение признака m_e, которое делит вариационный ряд пополам. Если объем выборки равен нечетному числу n=2к+1, то медиана является центральным значением признака, т.е. m_e=х_к+1. Если объем выборки равен четному числу n=2к, то медианой является среднеарифметическое двух центральных значений, т.е. m_e=(х_к+х_к+1)/2.

Пример 2. Получена выборка объемом n = 14. Признак имеет следующие значения 1, 1, 2, 2, 3, 3, 3, 5, 5, 5, 5, 6, 6, 8. Частотное распределение имеет вид:

Х
n

Тогда

= ,

m_o=5,

m_e= .

Каждая мера центральной тенденции обладает характеристиками, которые делают ее ценной в определенных условиях.

Для номинативных данных подходящей мерой центральной тенденции является мода – та градация номинативной переменной, которая встречается наиболее часто.

Для других переменных, распределения которых унимодальное и симметричное, мода, медиана и среднее совпадают. Чем больше отклонение от симметричности, тем больше расхождение между значениями этих мер. По этому расхождению можно судить о том, насколько симметрично или асимметрично распределение.

Наиболее очевидной и часто используемой мерой центральной тенденции является среднее значение. Но его использование ограничивается тем, на его величину влияет каждое отдельное значение. Если какое-нибудь значение увеличится (уменьшится) на С, то и среднее увеличится (уменьшится) на С/n. Т.е. среднее значение очень чувствительно к экстремальным значениям переменной. На величину же моды и медианы величина каждого отдельного значения не влияет.

Например, если в выборке объемом n утроить наибольшее значение, то не изменится ни мода, ни медиана. Величина же среднего возрастет.

Пример. Если 9 человек имеют месячный доход от 800 тысяч до 900 тысяч рублей, со средним 870 тысяч рублей, а доход десятого составляет 1,5 миллиона рублей, средний доход для всех 10 человек составит 933 тысячи рублей. Эта цифра не позволяет судить о всей группе, и в качестве меры центральной тенденции следовало бы брать медиану или моду.

Меры центральной тенденции чаще используются для сравнения групп по уровню выраженности признака. Если выполняются следующие условия, то можно сравнивать выборочные средние:

· группы достаточно большие, чтобы судить о форме распределения;

· распределения симметричны;

· отсутствуют экстремальные значения.

Если хотя бы одно из условий не выполняется, то следует ограничиться модой или медианой. Альтернативой является общее ранжирование данных всех групп и сравнение средних, вычисленных для рангов этих групп.

Помимо мер центральной тенденции в психологии часто используются меры положения, которые называются квантилями распределения. Квантиль – это значение признака, которое делит всю совокупность упорядоченных измерений (вариационный ряд) на группы с известным соотношением их численности. Например, медиана делит на равные части. Кроме медианы часто используются процентили и квартили.

Процентили – это 99 значений признака (Р₁,…, Р₉₉), которые делят вариационный ряд на 100 частей, равных по численности. Определяют процентиль следующим образом. Например, при определении 10-го процентиля Р₁₀, отсчитывают 10% испытуемых, имеющих наименьшую выраженность в упорядоченном ряду значений. Р₁₀ будет соответствовать тому значению признака, который отделяет эти 10% от остальных 90% (аналогично как и медиана).

Квартили – это 3 значения признака (Р₂₅, Р₅₀, Р₇₅), которые делят все значения на 4 равные по количеству части, поэтому они и соответствуют 25-му, 50-му и 75-му процентилю. Р₅₀ соответствует медиане.

В примере 2: Т.к. m_e Р₅₀=4, а Р₂₅=2, Р₇₅=5.

Процентили и квартили используются для определения частоты встречаемости тех или иных значений (или интервалов) измеренного признака или для выделения подгрупп и отдельных испытуемых, наиболее типичных или нетипичных для данного множества наблюдений.

 

2. Меры центральной тенденции говорят нам о концентрации группы значений на числовой шкале, т.е. отражают уровень выраженности измеренного признака. В этом случае пренебрегают различиями, существующими между отдельными значениями. Для измерения вариации оценок внутри группы требуются другие описательные статистики - меры изменчивости, которые и определяют численное выражение величины межиндивидуальной вариации признака.

Наиболее простой мерой является размах, измеряющий на числовой шкале расстояние, в пределах которого изменяются оценки. Рассматривают два типа размаха.

Исключающий - это разность максимального и минимального значений: R=x_max - x_min.

Включающий – разность между естественной верхней границей интервала, содержащего максимальное значение, и естественной нижней границей интервала, включающего минимальное значение.

Например, рост пяти мальчиков измерен с точностью до ближайшего см: 150, 155, 157, 165, 168. Фактический рост самого низкого находится где-то между 149,5 и 150. И действительная нижняя граница равна 149,5 см. Аналогично верхняя – 168,5 см. Таким образом, включающий размах равен 168,5 – 149,5 =19 см.

Исключающий размах: 168 – 150 = 18 см.

Исключающим размахом является расстояние между минимальным и максимальным имеющимися значениями, что позволяет исключить возможное значение, находящееся выше максимального или ниже минимального.

Размах является довольно грубой, но общераспространенной мерой изменчивости. Она не всегда точно отражает размах варьирования значений, т.к. на нее влияют экстремальные значения.

 

Одной из основных мер изменчивости рассматривают дисперсию – среднеарифметическое квадратов отклонения значений признака от своего среднего. Если все значения признака Х в выборке объемом n различны, т.е. х₁, х₂,…х_n, то

 

Если же значение х₁ встречается n₁ раз, х₂ – n₂ раза, … х_к – n_к раз, причем Σ n_i = n, тогда

 

 

Чем больше изменчивость в данных, тем больше отклонения значений от среднего (больше разброс значений), тем больше величина дисперсии.

Различают теоретическую дисперсию для генеральной совокупности (обычно она не вычисляется) и эмпирическую, выборочную,которая служит для оценки генеральной дисперсии. В качестве более точной (несмещенной) оценки рассматривают выборочную исправленную дисперсию:

 

Среднеквадратичным (стандартным) отклонением называют квадратный корень из дисперсии:

или

На практике чаще используют стандартное отклонение, т.к. оно выражает изменчивость в исходных единицах измерения признака, а дисперсия в квадратах исходных единиц.

Вычисление дисперсии можно упростить, используя следующую теорему:

Дисперсия равна разности среднего квадратов значений признака и квадрата общей средней, т.е. D= - ².

 

Для примера 2:

1-й способ.

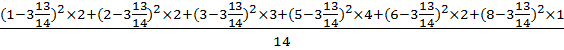= = ≈4,07.Аналогично, .

Тогда = ≈ 2,02, ≈ 2,09.

2-й способ.

=

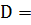19,5 – ² ≈4,07.

 

Свойства дисперсии:

1. Если измеренный признак имеет только одно значение, то дисперсия равна нулю, т.е. D(С)=0.(изменчивость в данных отсутствует)

2. При прибавлении (вычитании) одного и того же числа к каждому значению признака дисперсия не меняется, т.е. D(Х+С)=D(Х).

Док-во: Σ[(х_i+C) – ( +C)]²=Σ (х_i– )².

P.S. Прибавление константы к каждому значению признака сдвигает график его распределения на эту константу, при этом меняется среднее (см. свойства), но не меняется разброс значений.

 

 

f

1

3 D₁=D₃, D₁<D₂

2

 

₁= _{2 3} X

Рис. 3.1.

3. При умножении каждого значения признака на константу С дисперсия увеличивается в С² раз, а стандартное отклонение – в С раз, т.е. D(СХ)=С² D(Х).

Док-во: Σ[(Cх_i) – (C )]²= С²Σ (х_i– )².

4. При объединении групп к внутригрупповой дисперсии каждой группы добавляется дисперсия, обусловленная различием между их средними. Чем больше различия между средними значениями, тем больше увеличивается дисперсия объединенных групп.

Пример 3. Если одна выборка содержит значения 1, 1, 1, 1, 1, а другая – значения 3, 3, 3, 3, 3, то D₁=D₂ =0. Если же объединить эти две выборки в одну, то D=1.

 

Пусть все значения количественного признака Х разбиты на несколько групп. Рассматривая каждую группу как отдельную совокупность, можно найти ее групповую дисперсию –дисперсию значений признака, принадлежащих группе, относительно групповой средней.

Внутригрупповой дисперсиейназывают средне арифметическое групповых дисперсий, «взвешенных» по объемам групп:

, где n_i – объемы групп.

Межгрупповой дисперсией –называют дисперсию групповых средних относительно общей средней:

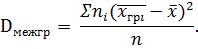
Общая дисперсия – дисперсия значений признака всей совокупности относительно общей средней.

Теорема: