Тема 2.3. Теория оценок (4 ч)

П Л А Н

1. Статистические оценки параметров распределения. Виды оценок.

2. Точечные оценки генерального среднего и генеральной дисперсии.

3. Интервальное оценивание. Точность и доверительная вероятность

интервальных оценок.

4. Доверительные интервалы для генерального среднего.

5. Доверительный интервал для генерального стандартного

отклонения. Точность измерения.

1. Статистика имеет дело с данными, подверженными случайной изменчивости. Поэтому нельзя указать совершенно точное значение параметров для генеральной совокупности, основываясь только на выборочных данных. Можем имееть только приближенные значения их. Термин «оценить» в статистике означает «указать приближенное значение».

Оцениванием в статистике называется указание приближенного значения интересующего нас параметра на основе наблюдаемых значений. Оценка – это правило вычисления приближенного значения параметра по наблюдаемым данным.

Методов для определения оценок параметров можно придумать достаточно много. Но для того, чтобы они давали оптимальные приближения к ним предъявляются определенные требования, такие как:

состоятельность оценки, т.е. если она сходится по вероятности к оцениваемому параметру при n→∞ ;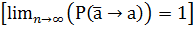

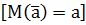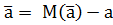несмещенность оценки, т.е. математическое ожидание ее должно равняться истинному значению параметра . Если , то Δ называется смещением или систематической ошибкой оценки.

эффективность оценки, которая при заданном объеме выборки имеет наименьшую возможную дисперсию.

Оценки параметров подразделяются на точечные и инт ервальные.

Точечная оценка параметра аопределяется одним числом 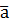и ее точность характеризуется дисперсией оценки.

Интервальная оценкаопределяется двумя числам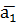и и , которые являются концами интервала, накрывающего параметр а с заданной вероятностью.

2. Пусть дана некотораяя генеральная совокупность объема N. Если из нее извлечены несколько выборок достаточно большого объема n₁, n₂ … n_к, для которых найдены выборочные средние , ,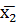… , 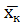то они все приблизительно равны между собой. В этом заключается свойство устойчивости выборочных средних. А значит, 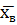можно принять за оценку генеральной средней. Она является несмещенной, состоятельной и эффективной.

В качестве точечной оценки генеральной дисперсии D_г можно принять выборочную D_в, но она является смещенной оценкой, т.е. 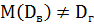. Получено, что 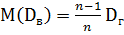. Поэтому несмещенной оценкой генеральной дисперсии является исправленная дисперсия s² (cм. 1.3.2. «Первичные описательные статистики»), а следовательно, оценкой стандартного отклонения является исправленное стандартное отклонение.

3. При небольшом объеме выборки точечные оценки могут значительно отличаться от оцениваемого параметра. Поэтому при небольшом объеме следует пользоваться интервальными оценками.

Если а – оцениваемый параметр, - его оценка, и задано некоторое δ>0, такое ,что 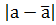<δ, то δ называетсяточностью оценки. Чем меньше δ, тем точнее оцениваение. Но нельзя категорически утверждать что оценка удовлетворяет данному неравенству, можно лишь говорить о вероятности, с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки параметра а называется вероятность γ, с которой осуществляется неравенство 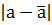<δ.

Обычно надежность задается наперед, причем γ≈1. Наиболее часто встречаются γ=0,95; γ=0,99; γ=0,999.

Иначе, надежность γ=Р( 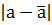<δ).

Из 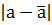<δ следует , что 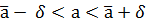. Тогда доверительная вероятность – это вероятность, с которой интервал ( 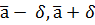) заключает в себе (покрывает) неизвестный параметр а.

Доверительным интервалом называют интервал ( 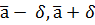), который покрывает неизвестный параметр с заданной надежностью γ.

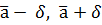– доверительные границы.

Метод доверительных интервалов разработал американский статистик Нейман, исходя из идей английского статистика Фишера.

4. Рассмотрим интервальное оценивание генерального среднего.

1-й случай. Пусть признак Х генеральной совокупности распределен нормально, причем среднеквадратичное отклонение σ этого распределения известно. Оценим неизвестное генеральное среднее по выборочной средней .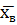

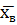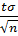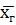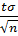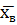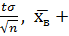
В теории вероятностей с помощью функции Лапласа было получено, что Р( - < < )=2Ф(t)=γ. Таким образом, с надежностью γ можно утверждать, что доверительный интервал ( - 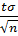) покрывает неизвестное генеральное среднее. Точность этой оценки - δ= 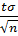. Значение t определяется из равенства 2Ф(t)=γ.

Ф(t)=γ/2, далее t находим по таблице значений функции Лапласа.

Пример. Некоторый признак Х имеет нормальное распределение с дисперсией D=9. Найти доверительный интервал для оценки генеральной средней 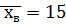, если объем выборки n=36 и надежность оценки γ=0,95.

Решение.

Ф(t)=γ/2=0,95/2=0,475. По таблице t=1,96, σ= 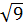=3, δ= 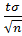= =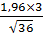0,98.

Тогда доверительный интервал (15-0,98; 15+0,98)=(14,02;15,98) с верроятностью 95% покрывает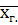

P.S. Генеральная средняя – постоянное значение, поэтому оно либо попадает в этот интервал (Р=1), либо нет (Р=0). Говоря о вероятности Р(/ 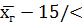0,98)=0,95, имеется в виду, что в 95% достаточно большого количества выборок определяются доверительные интервалы, в которых ген. средняя заключена, и лишь в 5% он может выйти за пределы этого интервала.

Если требуется оценить генеральную среднюю с заданной точностью δ и надежностью γ, то минимальный объем выборки, который обеспечит эту точность, находят следующим образом:

δ= 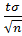=› = 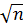=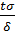› n= .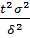

2-й случай. Но чаще всего встречается ситуация, когда дисперсия D, а значит и среднеквадратичное отклонение σ, для нормально распределенной переменной Х неизвестны.

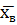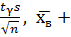
Тогда с помощью распределения Стьюдента был найден доверительный интервал для оценки генеральной средней с надежностью γ ( - ), где t_γ находят по таблицам по значениям n и γ, а s – исправленное среднеквадратичное отклонение, найденное для данной выборки.

P.S. 1. Данные выводы более точны для n>30, т.к. при этом условии распределение Стьюдента стремится к нормальному.

При n<30 интервал получается более широкий, чем интересует нас.

2. Данные выводы используются и для оценки измеряемой величины, т.е. истинное значение измеряемой величины можно оценить по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов.

Пример. По данным 9-ти равноточных измерений физической величины найдены 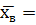42,3 и s= 5,0. Оценить истинное значение измеряемой величины с точностью 0,95.

Решение. Истинное значение измеряемой величины равно математическому ожиданию (или среднему выборочных измерений). Поэтому по γ=0,95 и n=9 найдем t_γ=2,31, тогда δ= 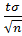=3,85, т.е. истинное значение измеряемой величины находится в интервале ( 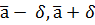)=(42,3 – 3,85; 42,3 + 3,85)… с вероятностью 0,95.

5. Пусть количественный признак Х генеральной совокупности распределен нормально. Необходимо оценить неизвестное генеральное стандартное отклонение по исправленному выборочному среднеквадратичному отклонению s.

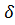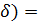Найдем доверительный интервал, покрывающий параметр σ с заданной надежностью γ, т.е. необходимо выполнение соотношения Р(/σ - s / < δ) = γ или Р(s - <σ<s+ γ.

Преобразуем 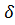s - <σ<s+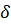

s (1 - 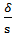)<σ<s(1+ 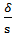), обозначим 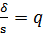, тогда

s (1 - 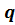)<σ<s(1+ ). (*)

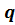По γ и n в таблице находятся значения .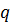

Из последнего неравенства (*) следует, что 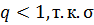>0. Но если 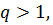то неравенство примет вид 0<σ<s(1+ ).

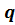В теории ошибок принято точность измерения (точность прибора) характеризовать с помощью среднеквадратичного отклонения σ случайных ошибок измерений. Для оценки σ также используют исправленное среднеквадратичное отклонение s.

Пример. По 15 равноточным измерениям найдено исправленное среднеквадратичное отклонение s=0,12. Найти точность измерений с надежностью 0,99.

Решение. По таблице по γ=0,99 и n=15 находим 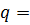0,73.

1, тогда 0,12(1 -0,73) < σ < 0,12(1 + 0,73)

0,03<σ<0,21.