Однофакторный дисперсионный анализ

 

После завершения шага 3 на экране должно присутствовать окно редактора дан-ных со строкой меню.

 

Шаг 4 В меню Анализ выберите команду Сравнение средних Однофакторный дисперсионный анализ. На экране появится диалоговое окно Однофак-торный дисперсионный анализ, показанное на рис. 13.1.

 

 

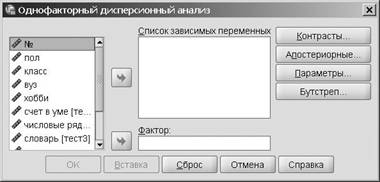
Рис. 13.1.Диалоговое окно Однофакторный дисперсионный анализ

186 Глава 13.Однофакторный дисперсионный анализ

 

 

Структура диалогового окна Однофакторный дисперсионный анализ вполне типич-на для большинства диалоговых окон SPSS. Слева мы видим список перемен-ных текущего файла данных. В правой части окна расположены кнопки: Апосте-риорные, Контрасты и Параметры, которые мы будем использовать при обработке. Список зависимых переменных предназначен для задания одной или нескольких зависимых переменных (в нашем примере будет использоваться единственная за-висимая переменная тест1). Зависимые переменные должны быть метрического типа. Если в списке указано несколько зависимых переменных, SPSS выполнит анализ для каждой из них. Под окном Список зависимых переменных находится поле Фактор, в котором нужно указать единственную независимую переменную, имеющую несколько градаций (в нашем случае — хобби). Таким образом, мы срав-ним результаты первого теста («счет в уме») для трех групп учащихся, различаю-щихся внешкольными увлечениями.

 

На шаге 5 мы будем сравнивать между собой средние значения переменной тест1 для каждой из выборок по уровням переменной хобби.

 

Шаг 5 После выполнения шага 4 должно быть открыто диалоговое окно Одно-факторный дисперсионный анализ, показанное на рис. 13.1. При необхо-димости повторите шаг 4 и выполните следующие действия.

 

в Щелкните сначала на переменной тест1, чтобы выделить ее, а за-тем — на верхней кнопке со стрелкой, чтобы переместить перемен-ную в Список зависимых переменных.

 

в Щелкните сначала на переменной хобби, чтобы выделить ее, а за-тем — на нижней кнопке со стрелкой, чтобы переместить перемен-ную в поле Фактор.

 

в Щелкните на кнопке OK, чтобы открыть окно вывода.

 

Существует два дополнительных действия, которые иногда желательно выполнять

 

А процессе анализа. Приведенная последовательность инструкций позволяет по-лучить результаты сравнения средних значений выборок, однако ни сами средние значения, ни результаты парного сравнения выборок в выводимых данных отобра-жены не будут. Первая проблема решается при помощи кнопки Параметры. Диало-говое окно Однофакторный дисперсионный анализ: Параметры, появляющееся после щелчка на этой кнопке, показано на рис. 13.2. Установка флажка Описательные статистики приведет к включению в выводимые данные всех средних значений, стандартных отклонений, стандартных ошибок, границ доверительных интервалов

 

А 95 %, а также минимумов и максимумов выборок. Флажок Проверка однород-ности дисперсии позволяет вывести информацию о степени пригодности данных к дисперсионному анализу, а с помощью флажка График средних можно построить диаграмму, на которой будут изображены средние значения для каждой выборки.

 

Парные сравнения

 

Нередко нас могут заинтересовать результаты парных сравнений уровней независи-мой переменной, и для этой цели в диалоговом окне Однофакторный дисперсионный

Пошаговые алгоритмы вычислений

 

 

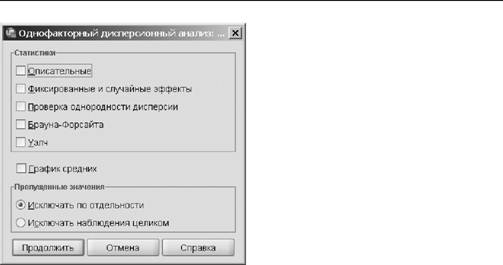
Рис. 13.2.Диалоговое окно Однофакторный дисперсионный анализ:Параметры

 

анализ предусмотрена специальная кнопка Апостериорные. Слово «апостериор-ные» означает, что эта процедура проводится после установления статистически достоверного результата однофакторного дисперсионного анализа. Если результа-ты дисперсионного анализа оказались статистически недостоверными, применение процедуры парных сравнений некорректно. При щелчке на кнопке Апостериорные открывается диалоговое окно Однофакторный дисперсионный анализ: Апостериор-ные множественные сравнения, приведенное на рис. 13.3. Это диалоговое окно с по-мощью флажков позволяет задать 14 критериев для выборок с одинаковой дис-персией и 4 критерия для выборок с разной дисперсией.

 

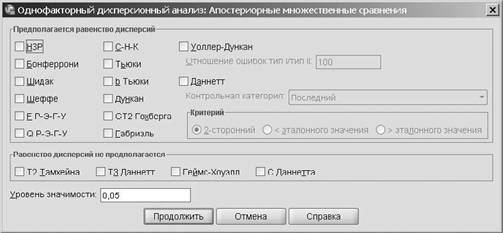
Рис. 13.3.Диалоговое окно Однофакторный дисперсионный анализ:

 

Апостериорные множественные сравнения

188 Глава 13.Однофакторный дисперсионный анализ

 

 

Большинство из указанных тестов используются очень редко, поэтому ниже при-ведены описания только для нескольких наиболее популярных.

 

ff НЗР (Наименьшая значимая разность) — этот критерий представляет собой со-вокупность t-критериев для всех возможных пар градаций фактора. Критерий наименьшей значимой разности является одним из самых «либеральных», по-скольку наиболее подвержен ошибкам. Например, если независимая перемен-ная имеет 5 уровней, то будет проведено 10 сравнений. При уровнях значимо-сти каждого из сравнений, равных 0,05, существует вероятность почти в 40 % того, что хотя бы один из тестов показал значимый результат случайно.

 

ff Бонферрони — этот критерий схож с критерием наименьшей значимой раз-ности, однако лишен недостатка, связанного с повторными проверками: в нем уровень значимости делится на число сравнений. Таким образом, критерий Бонферрони является более «консервативным».

 

ff Шеффе — критерий еще более «консервативный», чем критерий Бонферрони (используется F-критерий вместо t-критерия).

 

ff Тьюки — критерий Тьюки использует статистику Стьюдента для определения различий между группами. Этот критерий часто применяется в случаях, когда исследуемый фактор имеет большое количество уровней.

 

Самыми консервативными из предложенных являются критерии Шеффе и Бон-феррони. Часто используется также критерий Тьюки, называемый еще критерием подлинной значимости (Honestly Significant Difference, HSD). Последний задает наименьшую величину разности средних значений выборок, которую можно счи-тать значимой. Например, если HSD = 2,5, а для двух выборок получены величины средних значений 3,7 и 6,3, то разность между ними, равная 2,6, согласно Тьюки, является значимой, поскольку она превышает величину HSD. При использовании критерия Тьюки программа SPSS также включает в вывод дополнительную стати-стическую информацию.

 

Необходимо отметить, что все описанные выше критерии (на самом деле, большин-ство критериев парных сравнений) применяются в предположении, что дисперсии всех ячеек равны. Исключение составляют 4 критерия, флажки для которых выде-лены в отдельную группу в нижней части диалогового окна Равенство дисперсий не предполагается, — они применяются в случаях, когда дисперсии ячеек разные.

 

В следующем примере мы проведем однофакторный дисперсионный анализ, а в выво­димые­ результаты включим описательные статистики и критерий одно-родности дисперсии. Для парных сравнений воспользуемся критерием Шеффе. Как и в предыдущем примере, зависимой переменной будет переменная тест1, а независимой — переменная хобби.

 

Шаг 5А После выполнения шага 4 должно быть открыто диалоговое окно Одно-факторный дисперсионный анализ, показанное на рис. 13.1. При необхо-димости повторите шаг 4 и выполните следующие действия.

 

с Щелкните сначала на переменной тест1, чтобы выделить ее, а за-тем — на верхней кнопке со стрелкой, чтобы переместить перемен-ную в Список зависимых переменных.

Пошаговые алгоритмы вычислений

 

 

с Щелкните сначала на переменной хобби, чтобы выделить ее, а за-тем — на нижней кнопке со стрелкой, чтобы переместить перемен-ную в поле Фактор.

 

с Щелкните на кнопке Параметры, чтобы открыть диалоговое окно

 

Однофакторный дисперсионный анализ: Параметры, показанное на рис. 13.2.

 

с Установите флажки Описательные, Проверка однородности дисперсии

 

и График средних, а затем щелкните на кнопке Продолжить, чтобы вернуться в диалоговое окно Однофакторный дисперсионный анализ.

 

с Щелкните на кнопке Апостериорные, чтобы открыть диалоговое окно

 

Однофакторный дисперсионный анализ: Апостериорные множественные сравнения), показанное на рис. 13.3.

 

с Установите флажок Шеффе и щелкните на кнопке Продолжить, чтобы вернуться в диалоговое окно Однофакторный дисперсионный анализ.

 

с Щелкните на кнопке OK, чтобы открыть окно вывода.

 

 

Контрасты

 

Верхняя кнопка в правой части окна Однофакторный дисперсионный анализ имеет название Контрасты. Она предназначена для вызова диалогового окна Однофак-торный дисперсионный анализ: Контрасты, представленного на рис. 13.4. Это окно позволяет осуществлять различные сравнения выборок по градациям независимой переменной. Так, вы можете сравнивать одну градацию с другой, одну градацию со всеми остальными или разбить все градации на две группы и затем сравнить их между собой. Сравнение сводится к применению модифицированного варианта t-критерия. Отметим, что применение метода контрастов не требует предваритель-ного получения статистически достоверного результата анализа ANOVA, в отличие от процедуры апостериорного множественного парного сравнения.

 

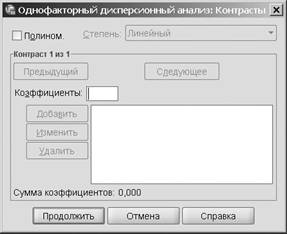
Рис. 13.4.Диалоговое окно Однофакторный дисперсионный анализ:Контрасты

190 Глава 13.Однофакторный дисперсионный анализ

 

 

и нашем примере независимая переменная хобби имеет три градации: 1 — спорт,

 

2 — компьютер, 3 — искусство. Для задания контраста предназначены поле и список Коэффициенты. Заполнение списка происходит следующим образом. Каждой гра-дации фактора вы должны сопоставить число, определяющее его роль в контрасте: отрицательное число соответствует одной группе, положительное число — другой группе, а ноль означает, что градация в сравнениях не задействована. При этом абсолютные величины коэффициентов неважны, но последние должны вводиться в порядке следования градаций и в сумме давать нулевое значение. Например, если вам необходимо сравнить увлекающихся спортом с остальными учащимися, вы можете закодировать градации последовательностью –2, 1 и 1, а если вы хо-тите сравнить увлекающихся спортом только с теми, кто увлекается искусством, необходимо задать последовательность 1, 0 и –1. Не забывайте, что сумма всех коэффициентов обязательно должна равняться 0.

 

Помещение чисел в список осуществляется путем ввода значения в поле справа от названия списка и щелчка на кнопке Добавить. Если нужно создать несколько «контрастов», то есть разбиений на группы, щелкните на кнопке Следующее справа от метки Контраст 1 из 1 и повторите описанную процедуру.

 

Следующий пример иллюстрирует применение контрастов: для сравнения уча-щихся, увлекающихся компьютером, с теми, кто имеет другие увлечения, а также для сравнения увлекающихся спортом с остальными учащимися.

 

Шаг 5Б После выполнения шага 4 должно быть открыто диалоговое окно Одно-факторный дисперсионный анализ, показанное на рис. 13.1. Если вы уже успели поработать с этим окном, очистите его щелчком на кнопке Сброс и выполните следующие действия.

 

и Щелкните сначала на переменной тест1, чтобы выделить ее, а за-тем — на верхней кнопке со стрелкой, чтобы переместить перемен-ную в список Зависимые переменные.

 

и Щелкните сначала на переменной хобби, чтобы выделить ее, а за-тем — на нижней кнопке со стрелкой, чтобы переместить перемен-ную в поле Фактор.

 

и Щелкните на кнопке Параметры, чтобы открыть диалоговое окно Одно-

 

факторный дисперсионный анализ: Параметры, показанное на рис. 13.2.

 

и Установите флажки Описательные, Проверка однородности дисперсии

 

и График средних, а затем щелкните на кнопке Продолжить, чтобы вернуться в диалоговое окно Однофакторный дисперсионный анализ.

 

и Щелкните на кнопке Апостериорные, чтобы открыть диалоговое окно

 

Однофакторный дисперсионный анализ: Апостериорные множественные сравнения, показанное на рис. 13.3.

 

и Установите флажок НЗР и щелкните на кнопке Продолжить, чтобы вернуться в диалоговое окно Однофакторный дисперсионный анализ.

 

и Щелкните на кнопке Контрасты, чтобы открыть диалоговое окно

 

Однофакторный дисперсионный анализ: Контрасты, представленное на рис. 13.4.

Представление результатов

 

 

В Нажмите клавишу Tab, чтобы перевести фокус ввода в поле Коэф-фициенты, введите число 1 и щелкните на кнопке Добавить, задав первое число в списке.

 

В Повторите предыдущее действие сначала для чисел –2 и 1, затем, щелкнув на кнопке Следующий, — для чисел –2, 1, 1, после чего щелкните­ на кнопке Продолжить, чтобы вернуться в диалоговое окно Однофакторный дисперсионный анализ.

 

10. Щелкните на кнопке OK, чтобы открыть окно вывода.

 

После выполнения шага 5 программа автоматически активизирует окно вывода. Для просмотра результатов вы при необходимости можете воспользоваться верти-кальной и горизонтальной полосами прокрутки. Обратите внимание на стандарт-ную строку меню в верхней части окна вывода: ее присутствие позволяет выпол-нять любые статистические операции, не переключаясь обратно в окно редактора данных.