 |
Главная |
Математическая статистика
|
из
5.00
|
Оглавление
Глава 1. Основные понятия теории вероятностей и математической статистики. 2
§ 1. Теория вероятностей. 2
§ 2. Математическая статистика. 6
Распределения, связанные с нормальным законом распределения и используемые в математической статистике. 9
Статистические оценки. 12
Глава 2. Имитационное моделирование. 15
§ 1. Основные понятия. 15
§ 2. Моделирование случайных величин методом Монте-Карло. 16
Метод Монте-Карло. Оценка погрешности. 16
Моделирование дискретных случайных величин. 17
Моделирование непрерывных случайных величин. 20
Вычисление определенного интеграла методом Монте-Карло. 21
Глава 3. Элементы корреляционного и регрессионного анализа. 24
§1. Элементы корреляционного анализа. 24
§2. Элементы регрессионного анализа. 28
§3. Решение задач регрессионного анализа с использованием пакета MatLab. 38
Глава 4. Временные ряды.. 42
§1. Основные понятия и задачи временных рядов. 42
§2. Прогнозирование. Экспоненциальное сглаживание. 52
Глава 1. Основные понятия теории вероятностей и математической статистики
Теория вероятностей
Введем математическое определение вероятности, используя аксиоматический подход А.Н. Колмогорова (1903 – 1987).
Определение: Вероятность – это счетно-аддитивная нормированная мера.
Здесь счетная аддитивность обозначает выполнение соотношения: 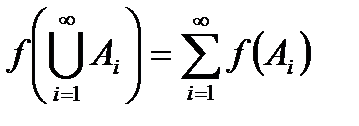 , если
, если 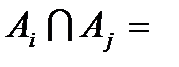 Ø,
Ø, 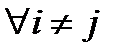 .Нормировка меры заключается в том, что ее значения (вероятность) принимает значения из
.Нормировка меры заключается в том, что ее значения (вероятность) принимает значения из 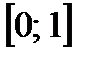 .Мера – вещественная неотрицательная функция счетной алгебры множеств.
.Мера – вещественная неотрицательная функция счетной алгебры множеств.
Пусть  – множество элементов
– множество элементов 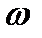 , которые называют элементарными событиями,а F –множество подмножеств из
, которые называют элементарными событиями,а F –множество подмножеств из  . Элементы множества F называют случайными событиями, а
. Элементы множества F называют случайными событиями, а  – пространством элементарных событий.
– пространством элементарных событий.
Алгебра F подмножеств множества  называется борелевской алгеброй, если все счетные суммы
называется борелевской алгеброй, если все счетные суммы 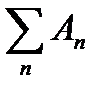 множеств
множеств 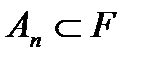 также принадлежат F. Борелевские алгебры называют также
также принадлежат F. Борелевские алгебры называют также 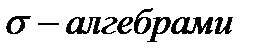 .
.
Вероятностная тройка 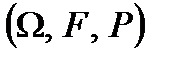 называется борелевским полем вероятностей, если соответствующая алгебра F, является борелевской.
называется борелевским полем вероятностей, если соответствующая алгебра F, является борелевской.
В теории вероятностей ограничиваются только борелевскими полями вероятностей.
Основной задачей теории вероятностей является нахождение вероятностей сложных событий по известным вероятностям простых событий.
В основе построения практически всех вероятностных схем теории вероятностей лежит схема испытаний Бернулли и ее обобщения.
Схема испытаний Бернулли:
Пусть проводится испытание, результатом которого могут быть два исхода – событие A («успех») и событие 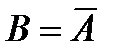 («неудача»). При этом считаем, что
(«неудача»). При этом считаем, что 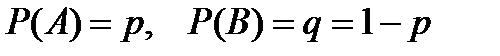 .
.
Вероятностная модель схемы испытаний Бернулли:
Рассмотрим вероятностную тройку 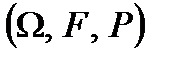 , где
, где 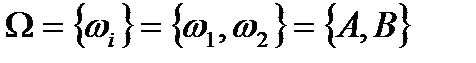 ,
, 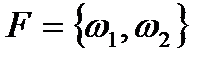 ,
,
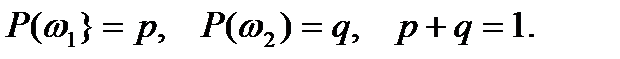
Пример: Бросание симметричной монеты (n=1)
Два исхода – «орел» (успех), «решка» (неудача), два события с вероятностями 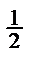 .
.
Пример: Последовательность независимых испытаний (n=2). Бросаем симметричную монету независимо два раза.
Четыре исхода (события) – «орел» «орел», «орел» «решка», «решка» «орел», «решка»«решка». Обозначим эти события соответственно через A, B, C, D. Тогда 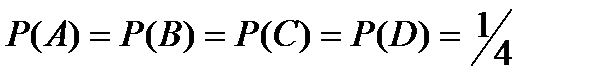 .
. 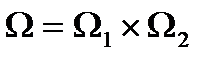 , где
, где 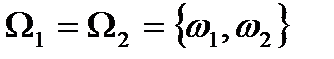 .
.
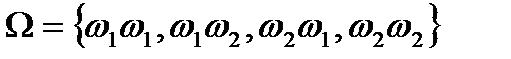 ,
, 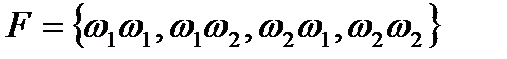 ,
, 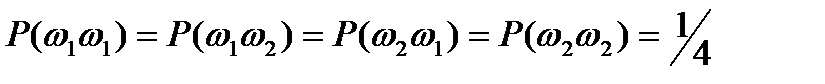 .
.
Пример: Бросание двух игральных костей. Найти вероятности события, что:
1. сумма выпавших очков нечетна и больше 5;
2. сумма выпавших очков четна и делится на 3.
В примере пространство элементарных событий состоит из 36 элементов – (1,1), (1,2), …, (6,6). Нашим условиям удовлетворяют следующие события (соответственно A, B):
в первом случае – 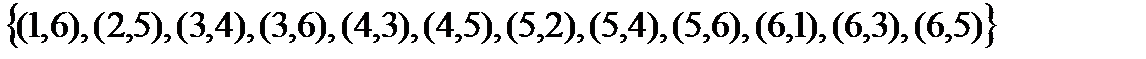 ;
;
во втором случае – 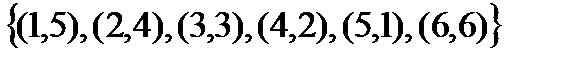 .
.
Пространство элементарных событий: 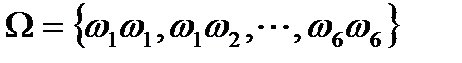 . Все события равновероятныи несовместны. Тогда
. Все события равновероятныи несовместны. Тогда 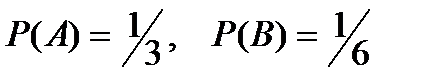 .
.
Проводя повторные испытания, каждое из которых удовлетворяет одной и той же схеме испытаний Бернулли, мы придем к формуле Бернулли.
Пусть проводится 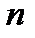 испытаний, в каждом из которых «успех» осуществляется с вероятностью
испытаний, в каждом из которых «успех» осуществляется с вероятностью 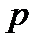 , «неудача» с вероятностью
, «неудача» с вероятностью 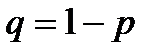 . Тогда вероятность того, что при
. Тогда вероятность того, что при 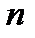 испытаниях будет ровно
испытаниях будет ровно 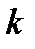 успехов, вычисляется по формуле:
успехов, вычисляется по формуле:
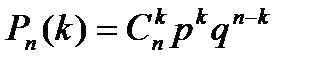 .
.
При больших значениях 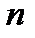 пользоваться формулой Бернулли становится достаточно сложно. Поэтому естественным является вопрос об асимптотической формуле нахождения вероятностей искомого события.
пользоваться формулой Бернулли становится достаточно сложно. Поэтому естественным является вопрос об асимптотической формуле нахождения вероятностей искомого события.
В 1730 г. Муавр нашел искомую асимптотическую формулу для частного случая 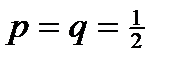 , а Лаплас в 1783 г. Обобщил формулу Муавра для произвольного
, а Лаплас в 1783 г. Обобщил формулу Муавра для произвольного 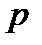 отличного от 0 и 1.
отличного от 0 и 1.
Локальная теорема Муавра-Лапласа
Если вероятность 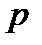 появления события
появления события 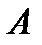 в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 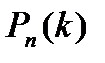 того, что событие
того, что событие 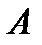 появится в
появится в 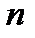 испытаниях ровно
испытаниях ровно 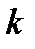 раз, приближенно равна (тем точнее, чем больше
раз, приближенно равна (тем точнее, чем больше 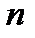 ) значению функции
) значению функции
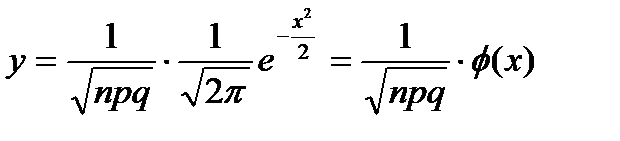 ,
,
где 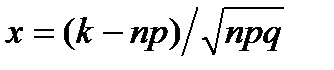 , а значения
, а значения 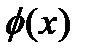 находят по статистическим таблицам.
находят по статистическим таблицам.
Для вычисления вероятности того, что при 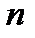 испытаниях событие
испытаниях событие 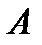 появится не менее
появится не менее 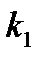 раз и не более
раз и не более 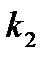 раз используют асимптотическую интегральную теорему Муавра–Лапласа.
раз используют асимптотическую интегральную теорему Муавра–Лапласа.
Интегральная теорема Муавра-Лапласа
Если вероятность 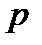 появления события
появления события 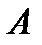 в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 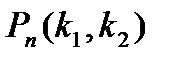 того, что событие
того, что событие 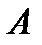 появится в
появится в 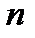 испытаниях от
испытаниях от 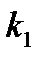 до
до 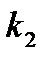 раз, приближенно равна определенному интегралу
раз, приближенно равна определенному интегралу
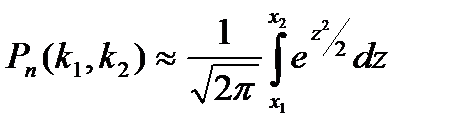 ,
,
где 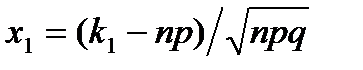 и
и 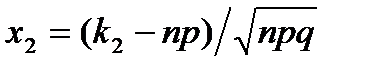 .
.
Распределение Пуассона
Пусть мы находимся в условиях предыдущего пункта, то есть, проводится 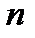 испытаний, в каждом из которых «успех» осуществляется с вероятностью
испытаний, в каждом из которых «успех» осуществляется с вероятностью 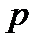 , «неудача» с вероятностью
, «неудача» с вероятностью 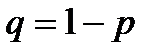 . Пусть вероятность события
. Пусть вероятность события 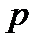 мала
мала 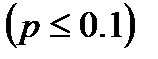 . Тогда вместо теоремы Муавра-Лапласа (нормального закона распределения) надо использовать теорему Пуассона (распределение Пуассона).
. Тогда вместо теоремы Муавра-Лапласа (нормального закона распределения) надо использовать теорему Пуассона (распределение Пуассона).
При этом делается важное допущение: произведение 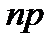 сохраняет постоянное значение, а именно
сохраняет постоянное значение, а именно 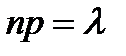 . Это означает, что среднее число появления события в различных сериях, то есть при различных значениях
. Это означает, что среднее число появления события в различных сериях, то есть при различных значениях 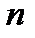 , остается постоянным. Тогда, справедливо соотношение:
, остается постоянным. Тогда, справедливо соотношение:
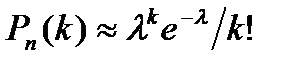 .
.
Геометрическое распределение
Пусть производятся независимые испытания, в каждом из которых «успех», событие 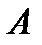 , осуществляется с вероятностью
, осуществляется с вероятностью 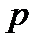 , «неудача» с вероятностью
, «неудача» с вероятностью 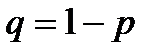 . Испытания заканчиваются, как только появится событие
. Испытания заканчиваются, как только появится событие 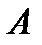 (то есть до первого успешного события).
(то есть до первого успешного события).
Пусть 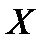 – дискретная случайная величина. Тогда справедливо соотношение:
– дискретная случайная величина. Тогда справедливо соотношение:
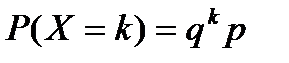 .
.
Полагая 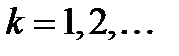 , в формуле, получим геометрическую прогрессию с первым членом
, в формуле, получим геометрическую прогрессию с первым членом 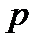 и знаменателем
и знаменателем 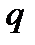 .
.
Отрицательное биномиальное распределение
Это распределение имеет место в тех случаях, когда последовательность испытаний обрывается сразу же после 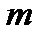 - го успеха. При этом рассматривают две случайные величины: случайная величина
- го успеха. При этом рассматривают две случайные величины: случайная величина 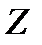 – число неудач, предшествовавших
– число неудач, предшествовавших 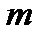 -му успеху, и случайная величина
-му успеху, и случайная величина 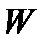 – общее число испытаний до
– общее число испытаний до 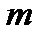 - го успеха (включая
- го успеха (включая 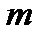 - й успех).
- й успех).
Определение: Однозначную действительную функцию 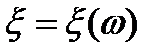 , определенную на пространстве элементарных событий
, определенную на пространстве элементарных событий  , называют случайной величиной, если при каждом выборе действительного числа
, называют случайной величиной, если при каждом выборе действительного числа 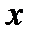 множество всех тех
множество всех тех 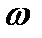 , для которых справедливо неравенство
, для которых справедливо неравенство 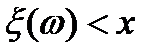 , принадлежит к системе множеств
, принадлежит к системе множеств 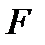 .
.
Эта функция 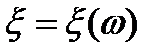 отображает множество
отображает множество  на множество
на множество 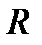 всех действительных чисел.
всех действительных чисел.
Если 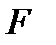 и
и 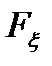 являются борелевскими алгебрами, тогда
являются борелевскими алгебрами, тогда 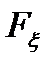 содержит все борелевские множества
содержит все борелевские множества 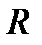 .
.
Определение:Функция 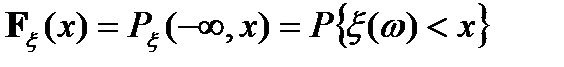 называется функцией распределения случайной величины
называется функцией распределения случайной величины 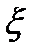 .
.
Свойства функции распределения:
-
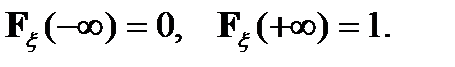
-
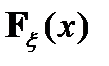 – неубывающая функция.
– неубывающая функция. -
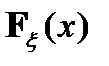 – непрерывна слева.
– непрерывна слева. -
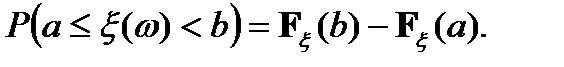
Закон больших чисел
Теорема, доказанная Якобом Бернулли (1713), и которая получила название «закон больших чисел», положила начало теории вероятностей как науки.
Теорема Бернулли: Если в каждом из 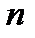 независимых испытаний вероятность
независимых испытаний вероятность 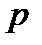 появления события
появления события 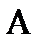 постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности
постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности 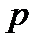 по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.
по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.
То есть, если 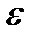 – сколь угодно малое положительное число, то при соблюдении условий теоремы справедливо равенство:
– сколь угодно малое положительное число, то при соблюдении условий теоремы справедливо равенство:

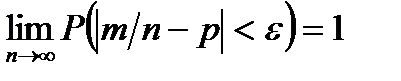 .
.
Таким образом, закон больших чисел в форме теоремы Бернулли можно считать обоснованием для использования классического определения вероятности.
Центральная предельная теорема (ЦПТ)
Содержательная формулировка ЦПТ: Если случайная величина 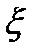 представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на сумму ничтожно мало, то
представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на сумму ничтожно мало, то 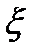 имеет распределение близкое к нормальному распределению.
имеет распределение близкое к нормальному распределению.
Пусть 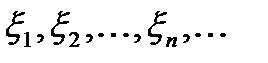 – последовательность независимых случайных величин, каждая из которых имеет конечное математическое ожидание и дисперсию:
– последовательность независимых случайных величин, каждая из которых имеет конечное математическое ожидание и дисперсию:
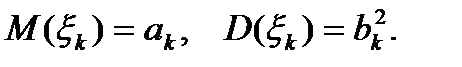
Пусть 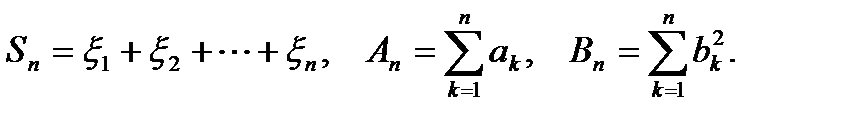
Говорят, что к последовательности 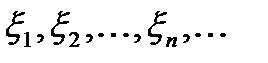 применима центральная предельная теорема, если при любом
применима центральная предельная теорема, если при любом 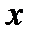 функция распределения нормированной суммы при
функция распределения нормированной суммы при 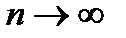 стремится к нормальной функции распределения:
стремится к нормальной функции распределения:
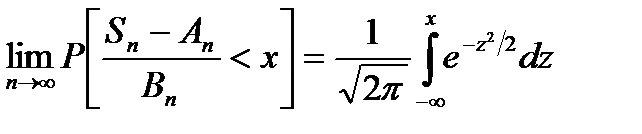 .
.
Математическая статистика
Статистика – любая функция от выборки (результатов наблюдения).
Генеральная совокупность – все множество однородных объектов, из которого по определенному правилу выбирается некоторое подмножество, называемое выборкой.
Под выборкой в широком смысле понимают конечную совокупность результатов наблюдений, представляющих собой независимые одинаково распределенные случайные величины.
Репрезентативная (представительная) выборка – выборка из генеральной совокупности, учитывающая качественные и количественные соотношения генеральной совокупности (генеральная совокупность «в миниатюре»).Понятие «репрезентативная выборка» широко используется в социологических, экономических, медицинских исследованиях.
Задачи, решаемые методами математической статистики, по своей сути, являются обратнымик задачам теории вероятностей.
Основная задача теории вероятностей – нахождение вероятностей сложных событий по вероятностям простых событий.
Задачи математической статистики – по вероятностям сложных событий нахождение вероятностей простых событий, нахождение оценок количественных характеристик случайной величины, оценок законов распределения.
Статистический критерий – случайная величина, по распределению которой мы либо принимаем соответствующую статистическую гипотезу или отвергаем ее с заданным уровнем значимости.
Эмпирическая функция распределения и оценка плотности распределения (гистограмма).
|
из
5.00
|
Обсуждение в статье: Математическая статистика |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

