 |
Главная |
Элементы регрессионного анализа
|
из
5.00
|
Рассмотрим математический аппарат регрессионного анализа – метод наименьших квадратов (систему нормальных уравнений).
Рассмотрим однофакторную линейную модель регрессии. Пусть дано n – объектов, которые характеризуются двумя величинами, одну из которых мы будем интерпретировать как результирующий показатель 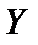 , зависящий от другого фактора
, зависящий от другого фактора 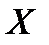 . Таким образом, мы ищем функцию
. Таким образом, мы ищем функцию 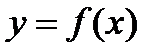 из определенного, нами выбранного класса функций. В качестве такого класса функций обычно выбирают класс степенных полиномов или тригонометрических полиномов (если есть периодичность).
из определенного, нами выбранного класса функций. В качестве такого класса функций обычно выбирают класс степенных полиномов или тригонометрических полиномов (если есть периодичность).
Пусть мы ищем приближающий полином первой степени: 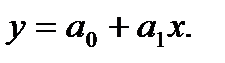 Рассмотрим функционал, который надо минимизировать:
Рассмотрим функционал, который надо минимизировать: 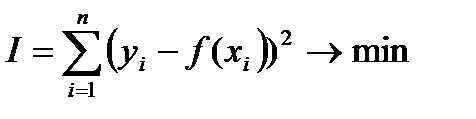 , где
, где 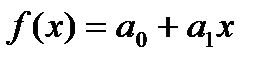 . Таким образом, надо найти два коэффициента
. Таким образом, надо найти два коэффициента 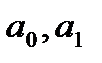 , так, чтобы минимизировать функционал
, так, чтобы минимизировать функционал 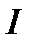 .
.
Для этого найдем частные производные по параметрам и приравняем их к нулю:

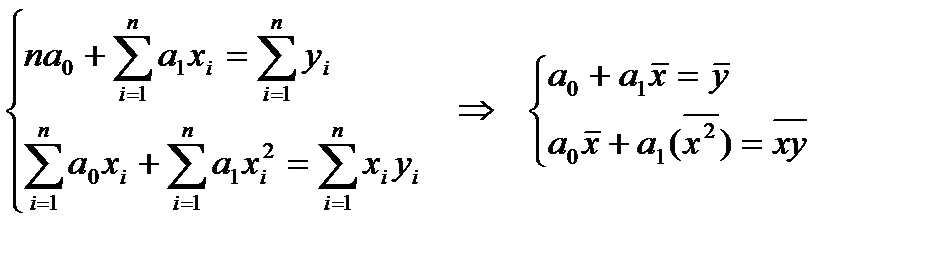 ,
,
где  .
.
Таким образом, имеем два уравнения и два неизвестных, и неизвестные входят в уравнения линейно. То есть, имеем СЛАУ (систему линейных алгебраических уравнений) 2-го порядка.
Запишем в матричном виде:
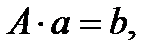 где
где 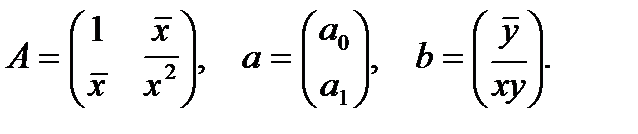
Домножая слева левую и правую части на 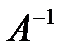 , получим решение
, получим решение 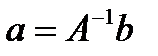 , то есть вектор коэффициентов,минимизирующий рассматриваемый функционал в смысле метода наименьших квадратов.
, то есть вектор коэффициентов,минимизирующий рассматриваемый функционал в смысле метода наименьших квадратов.
Уравнение однофакторной линейной регрессии можно записать и через статистические характеристики рассматриваемых случайных величин:
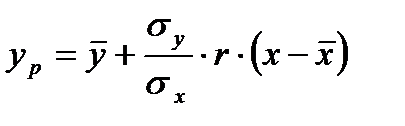 ,
,
где 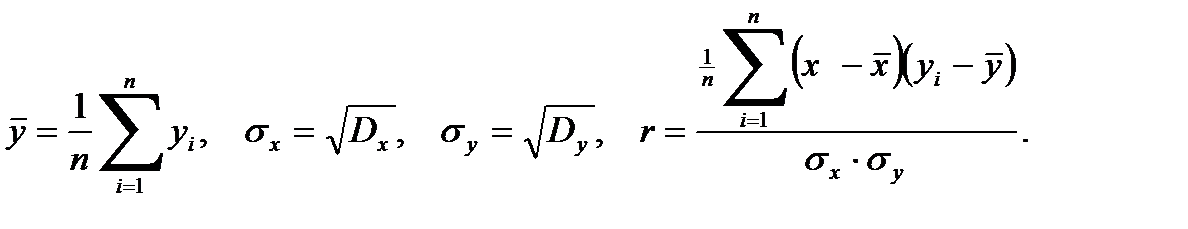
Как правило, в статистике рассматривают линейные, относительно входящих в уравнение параметров, регрессии, которые относятся к линейному регрессионному анализу.
В частности к таким уравнениям относятся и уравнения вида:
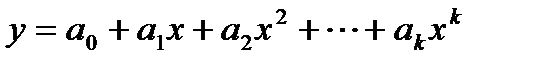 .
.
Величину  называют остаточной дисперсией. Если ее значение «большое», то приближение считается плохим, и рекомендуется перейти к полиному более высокого порядка.
называют остаточной дисперсией. Если ее значение «большое», то приближение считается плохим, и рекомендуется перейти к полиному более высокого порядка.
Линейный регрессионный анализ – линейный по параметрам (коэффициентам).
Стандартные модели линейного регрессионного анализа:
- Однофакторная линейная регрессия.
- Однофакторная полиномиальная регрессия.
- Многофакторная линейная регрессия.
Рассмотрим модель однофакторной полиномиальной регрессии.
Пусть дано 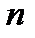 объектов, заданными выборочными значениями:
объектов, заданными выборочными значениями:
| X | 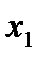
| 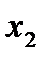
| … | 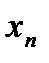
|
| Y | 
| 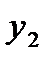
| … | 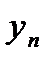
|
Рассмотрим функционал вида:
 . Но в качестве функции будем брать полином соответствующей степени:
. Но в качестве функции будем брать полином соответствующей степени: 
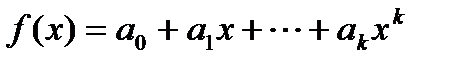 .
.
Тогда:
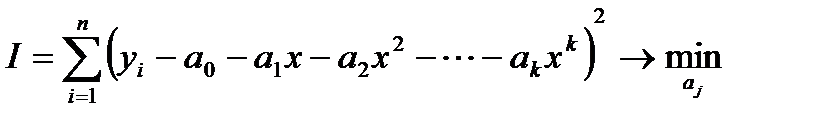 .
.
Возьмем частные производные, приравняем к нулю и приведем к виду:
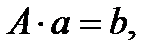 где
где 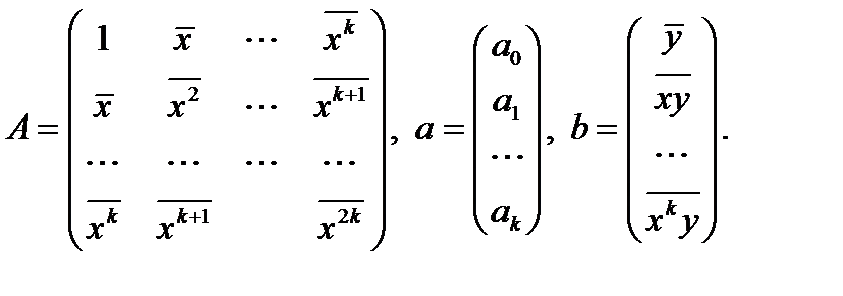
Решая эту систему линейных алгебраических уравнений, получим вектор 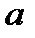 .
.
Множественная линейная регрессия
Берем 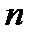 объектов, каждый из которых характеризуется
объектов, каждый из которых характеризуется 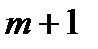 случайными величинами.
случайными величинами.
| Y | 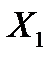
| 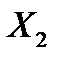
| 
| 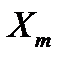
|
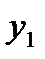
| 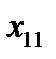
| 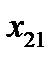
| 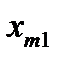
| |

| 
| 
| 
| 
|
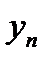
| 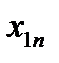
| 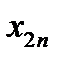
| 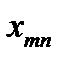
|
Зависимость между результирующим показателем 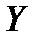 и совокупностью
и совокупностью  будем искать в виде:
будем искать в виде:
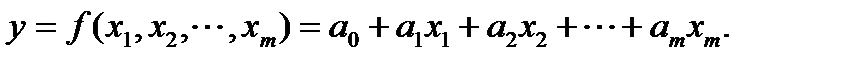

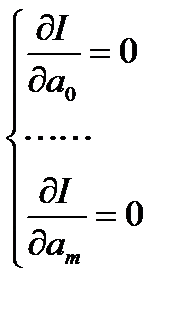
Известно, что регрессия проходит через точку 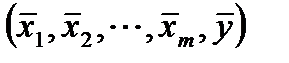 , то есть
, то есть
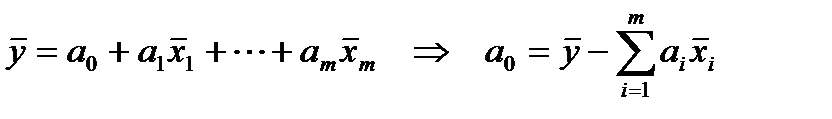
СЛАУ запишем в виде:
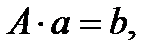 где
где 
Замечание: Коэффициент корреляции – нормированный, смешанный момент второго порядка, является мерой линейной зависимости.
Из независимости следует некоррелированность, обратное, в общем случае, неверно (верно, если две случайные величины распределены по нормальному закону распределения).
Пример: Из некоррелированности не следует независимость.
Рассмотрим случайную величину 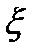 , распределенную по равномерному закону на интервале
, распределенную по равномерному закону на интервале  и две случайные величины
и две случайные величины  , которые связаны соотношением
, которые связаны соотношением 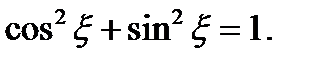 Показать, что коэффициент корреляции равен 0.
Показать, что коэффициент корреляции равен 0.
Задачи, связанные с моделями регрессий (для примера – линейная однофакторная регрессия)
1. Найти коэффициенты регрессии.
2. Определить, значимы ли эти коэффициенты.
3. Нахождение вида оптимальной модели.
4. Адекватность модели.
Первый пункт решают с использования МНК.
Для решения задачи о значимости коэффициента используют элементы дисперсионного анализа.
Утверждение: Для метода наименьших квадратов справедливо разложение:
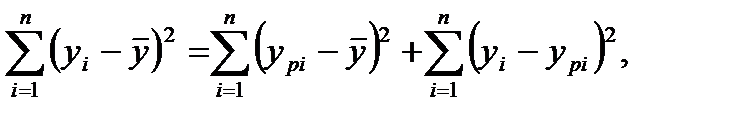
где первая сумма в правой части – сумма квадратов, обусловленная регрессией, вторая сумма – остаточная сумма квадратов.
Доказательство: Рассмотрим в качестве иллюстрации подхода случай однофакторной полиномиальной регрессии.
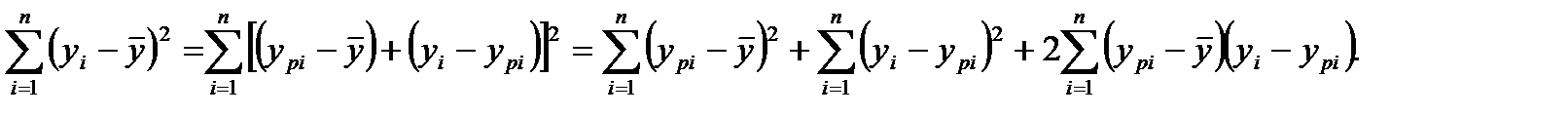
Рассмотрим удвоенное произведение:
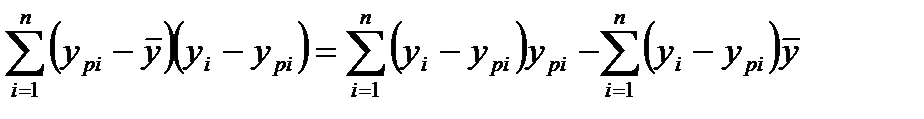 .
.
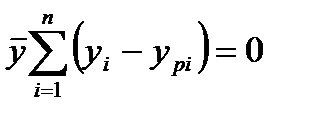 в силу "нормальных уравнений".
в силу "нормальных уравнений".
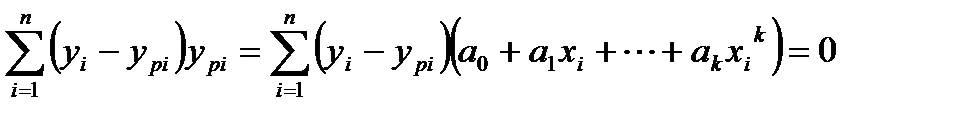
 в силу "нормальных уравнений".
в силу "нормальных уравнений".
Если остаточная сумма квадратов равна 0, то это означает, что регрессия проходит через выборочные точки. То есть, чем меньше остаточная сумма квадратов, а соответственно сумма квадратов регрессии, обусловленная регрессией, тем лучше.
Пусть у нас есть функция регрессии 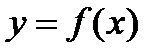 . Рассмотрим гипотезу о значимости регрессии, т.е.:
. Рассмотрим гипотезу о значимости регрессии, т.е.:
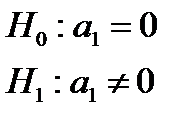
Для решения такой задачи используют таблицу дисперсионного анализа:
| Источниквариации | Сумма квадратов | Степени свободы | Средний квадрат |
| Регрессия | 
| 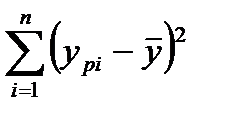
| |
| Остаток | 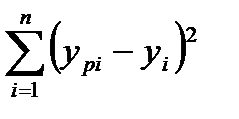
|

|  
|
| Общая вариация (дисперсия) | 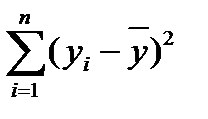
|
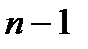
| 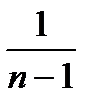 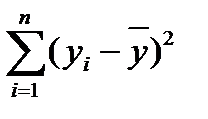
|
В качестве критерия рассмотрим критерий Фишера:
 .
.
Для нулевой гипотезы 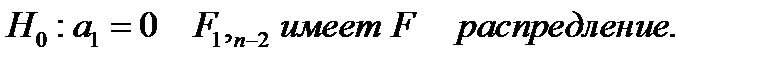
Если значение 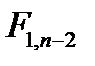 достаточно велико, то гипотезу
достаточно велико, то гипотезу 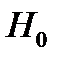 отклоняем. То есть, в этом случае коэффициент
отклоняем. То есть, в этом случае коэффициент 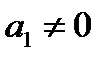 и, следовательно, регрессия значима.
и, следовательно, регрессия значима.
Пример:
| X | ||||
| Y |
Решение:
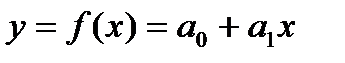 .
.
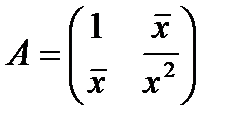 ;
;  ;
;  .
.
Вычисления в MATLAB:
clc
x=[1 3 4 5];
y=[10 20 18 20];
xc=mean(x);
yc=mean(y);
xyc=mean(x.*y);
xc2=mean(x.*x);
A=[1 xc; xc xc2]
b=[yc;xyc]
a=inv(A)*b
y1=a(1,1)+a(2,1)*x
%Суммаквадратоввариации
SS=sum((y-yc).^2)
SSO=sum((y-y1).^2)
SSR=SS-SSO
SSRK=SSR
SSOK=SSO/2
F=SSRK/SSOK
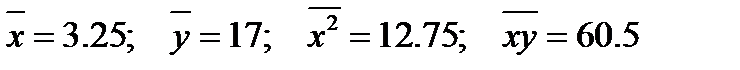
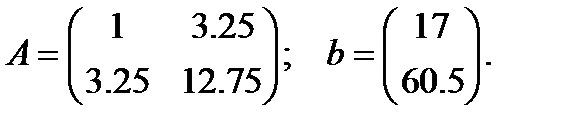
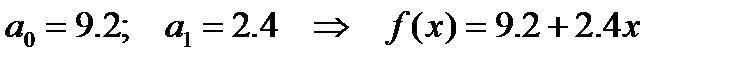
Регрессия = 50.4;
Остаток = 17.6;
Общая вариация = 68.
Средние квадраты:
регрессии – 50.4;
остатка – 8.8;
общей вар. – 22. (6)
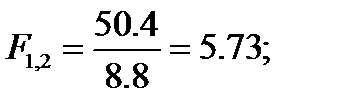 Смотрим таблицу критических точек Фишера. Пусть уровень значимости
Смотрим таблицу критических точек Фишера. Пусть уровень значимости 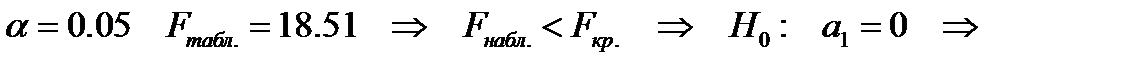 регрессия не значима.
регрессия не значима.
Если для каждого 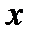 имеется несколько повторных наблюдений, то адекватность подгонки измеряется статистически. Так, если линия регрессии адекватна данным, то среднее
имеется несколько повторных наблюдений, то адекватность подгонки измеряется статистически. Так, если линия регрессии адекватна данным, то среднее 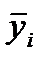 будет лежать близко к
будет лежать близко к  и, соответственно величина
и, соответственно величина 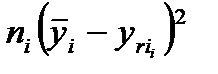 будет мала.
будет мала.
Если аппроксимация плохая, то значение будет велико.
Можно ввести меру неадекватности: 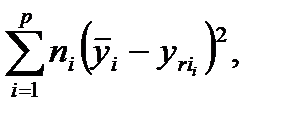 где
где 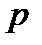 – количество разных значений
– количество разных значений 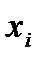 .
.
Тогда справедливо утверждение, что сумма квадратов остатка делится на 2 части:
1. неадекватность;
2. чистая ошибка, которая равна разности суммы квадратов остатка и неадекватности.
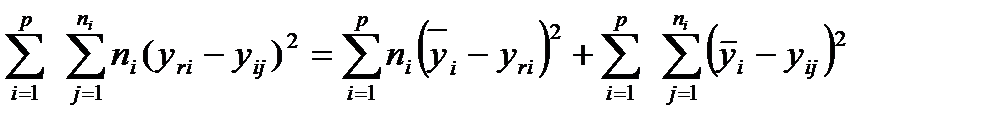
В качестве проверки неадекватности применяют критерий:
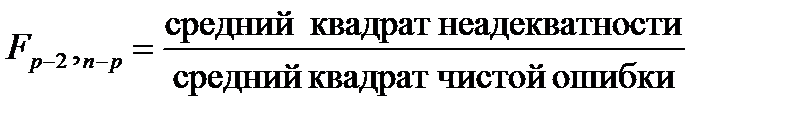 .
.
Если 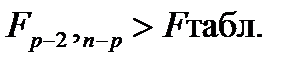 с определенным уровнем значимости, то аппроксимация плохая.
с определенным уровнем значимости, то аппроксимация плохая.
Средний квадрат неадекватности:
 .
.
Пример: Неадекватность (прямая линия)
| 
| 
| ||||
| 5 | ||||||
| 4 | ||||||
| 5 | ||||||
| 5 | ||||||
| 5 |
Дисперсионный анализ неадекватности:
Вычисления в MATLAB:
x=[ 10 10 10 10 10 20 20 20 20 35 35 35 35 35 40 40 40 40 40 60 60 60 60 60]
y1=[5 6 5 6 7]
y2=[12 13 14 13]
y3=[17 19 16 15 15]
y4=[18 20 21 18 20]
y5=[17 19 16 14 16]
xx=[10 20 35 40 60]
xc=mean(x)
y=[y1 y2 y3 y4 y5]
y1c=mean(y1)
y2c=mean(y2)
y3c=mean(y3)
y4c=mean(y4)
y5c=mean(y5)
n1=length(y)
yc=mean(y)
ssy=sum((y-yc).^2)
n=[length(y1) length(y2) length(y3) length(y4) length(y5)]
yy=[y1c y2c y3c y4c y5c]
x2c=mean(x.^2)
xyc=mean(x.*y)
A=[1 xc; xc x2c]
b=[yc; xyc]
a=inv(A)*b
y1=a(1,1)+a(2,1)*x
SSO=sum((y-y1).^2)
SSR=sum((y1-yc).^2)
yr=a(1,1)+a(2,1)*xx
SSRN=sum(n.*(yr-yy).^2)
SSHO=SSO-SSRN
SSOK=SSO/22
SSRNK=SSRN/3
SSHOK=SSHO/19
F=SSRNK/SSHOK
fprintf('F-критерий критич. %7.4f\n',F)
| Источник вариации | сумма квадратов | с. с. | ср. кв. | ||||
| Регрессия | 323.52 | 323.52 | |||||
| неадекватность | 218.58 | 72.86 | |||||
| Остаток | чистая ошибка | 254.98 | 36.40 | 11.59 | 1.92 | ||
| Общая вариация | 578.5 | - |
Для проверки на неадекватность вычислим:
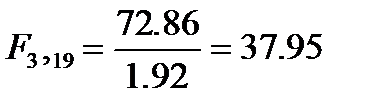
Результат высокозначим. Таким образом, делаем вывод, что найденная прямая плохо аппроксимирует данные.
|
из
5.00
|
Обсуждение в статье: Элементы регрессионного анализа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

