 |
Главная |
Элементы корреляционного анализа
|
из
5.00
|
Математической основой регрессионного анализа является метод наименьших квадратов (МНК). В вероятностно-статистическом смысле регрессия – это условное математическое ожидание. Термин регрессионного анализа ввел Френсис Гальтон (1822-1911) в связи с его работой по изучению изменения роста высоких родителей и их потомков. В настоящее время под регрессией понимают стремление к среднему в смысле метода наименьших квадратов при решении задач прогнозирования (экстраполирования).
Меры связи и формы зависимости случайных величин.
Основополагающим понятием, на котором строится математическая теория корреляции, является понятие стохастической связи между случайными величинами. Само понятие стохастической связи основывается на определении случайной величины и должно быть строго отделено от понятия функциональной зависимости.
Рассмотрим вопрос о различии понятий стохастической зависимости и функциональной зависимости.
Говорят, что переменная величина  функционально зависит от
функционально зависит от 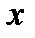 , или находится с
, или находится с  в функциональной связи, когда каждому из рассматриваемых значений
в функциональной связи, когда каждому из рассматриваемых значений 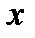 соответствует одно определенное значение. Функциональные связи в реальной жизни встречаются довольно редко. Гораздо чаще, рассматривая зависимости между действительно наблюденными величинами, мы встречаемся со статистическими связями, которые характеризуются тем, что когда
соответствует одно определенное значение. Функциональные связи в реальной жизни встречаются довольно редко. Гораздо чаще, рассматривая зависимости между действительно наблюденными величинами, мы встречаемся со статистическими связями, которые характеризуются тем, что когда  связано с
связано с 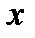 статистически, то всякому заданному значению
статистически, то всякому заданному значению 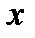 соответствует не одно значение
соответствует не одно значение  , а распределение значений
, а распределение значений  , изменяющееся вместе с изменением
, изменяющееся вместе с изменением 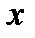 .
.
В реальной жизни переменные, находящиеся в функциональной зависимости, преобразуются в случайные переменные, состоящие в стохастической связи, из за данных, связанных с погрешностями измерений, и из за того, что не учитывается влияние не включенных в рассмотрение неслучайных факторов. Таким образом, при исследовании переменных, состоящих в стохастической связи, результаты должны интерпретироваться по-разному. Иногда стохастическая связь является лишь завесой, за которой скрывается интересующая нас функциональная зависимость. Иногда же изучению подлежит стохастическая связь, как таковая. В соответствии с целью исследования должны выбираться и соответствующие подходы и математические методы. Так, если речь идет о том, чтобы посредством изучения стохастической связи дойти до закона функциональной зависимости между интересующими исследователя величинами, то исследователь должен прибегать к методам "сглаживания". Если же ставится задача нахождения стохастической связи между случайными величинами, то тогда необходимо пользоваться методами теории корреляции. Таким образом, необходимо четко представлять себе постановку задачи, то есть какая задача решается: восстановление неизвестной функциональной зависимости по выборочным данным или нахождении корреляционной зависимости выраженной в виде регрессии. Методы нахождения зависимостей в этих двух случаях могут совпадать, но результаты должны интерпретироваться совершенно по-разному.
Когда условное распределение  меняется вместе с изменением
меняется вместе с изменением 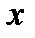 , мы будем говорить, что
, мы будем говорить, что  стохастически зависит от
стохастически зависит от 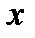 . Если же условное распределение
. Если же условное распределение  остается неизменным для всех значений
остается неизменным для всех значений 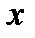 , говорят, что
, говорят, что  стохастически не зависит от
стохастически не зависит от 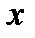 .
.
При исследовании связи между случайными величинами общая статистическая задача заключается в полном изучении их распределения, представляемого в виде корреляционной таблицы. И в этом изучении особый интерес представляет задача об исследовании связи между условными математическими ожиданиями одних случайных величин и соответствующими значениями других.
Если можно представить связь  и
и 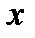 в виде уравнения:
в виде уравнения:
 ,
, 
где 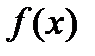 представляет определенную однозначную функцию, дающую возможность для
представляет определенную однозначную функцию, дающую возможность для  находить соответствующие
находить соответствующие  , то это уравнение называется уравнением регрессии
, то это уравнение называется уравнением регрессии  на
на 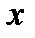 . Оно должно возможно точнее выравнивать наблюденное распределение условных средних.
. Оно должно возможно точнее выравнивать наблюденное распределение условных средних.
При рассмотрении корреляционной связи  и
и 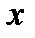 необходимо рассматривать две задачи:
необходимо рассматривать две задачи:
- определение формы корреляционной связи, то есть определение вида функций в уравнениях регрессий.
- определение силы, или степени связанности
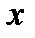 и
и  этими формами.
этими формами.
При этом, когда корреляционная связь не совершенно точна, можно ставить вопрос о ее точности, который существенно отличается от вопроса о силе связанности 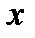 и
и  . Таким образом рассмотрим вопросы об определении меры линейной и нелинейной связанности двух статистических величин и нахождении кривых регрессий.
. Таким образом рассмотрим вопросы об определении меры линейной и нелинейной связанности двух статистических величин и нахождении кривых регрессий.
Рассмотрим статистическую совокупность  – двумерное статистическое распределение случайных величин
– двумерное статистическое распределение случайных величин  , заданное выборочными значениями (объем выборки =n). Заменяя интервалы, на которые разбиты
, заданное выборочными значениями (объем выборки =n). Заменяя интервалы, на которые разбиты 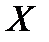 и
и 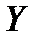 их серединами, можно представить двумерное распределение следующей таблицей:
их серединами, можно представить двумерное распределение следующей таблицей:
| X Y | 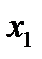
| 
| 
| 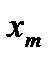
| |

| 
| 
| 
| 
| |

| 
| 
| 
| 
| |

| 
| 
| |||
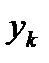
| 
| 
| 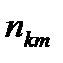
| 
| |
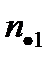
| 
| 
| 
| n |
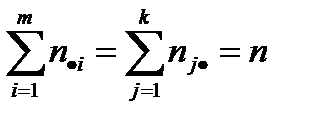
По таблице можем найти:
- условные средние;
- полные средние (для
 и
и 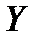 );
); - условные дисперсии;
- межгрупповые дисперсии;
- полные дисперсии.
Условное среднее(например,  при условии
при условии 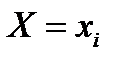 ):
): 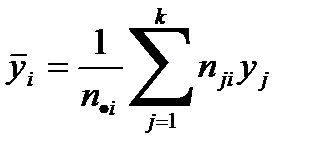
Полные средние: 
Условные дисперсии (например,  при условии
при условии 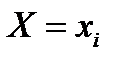 ):
): 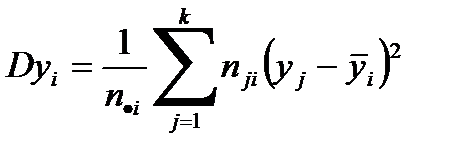 .
.
Межгрупповые дисперсии: 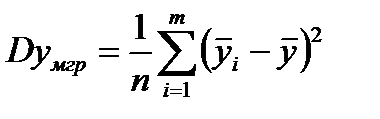 .
.
Полные дисперсии:  .
.
Основная теорема дисперсионного анализа: Общая дисперсия равна сумме межгрупповой и внутригрупповой дисперсий:
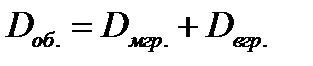
Рассмотрим крайние случаи:
Пусть  все условные дисперсии = 0, по
все условные дисперсии = 0, по  разброса нет, все значения для каждого
разброса нет, все значения для каждого 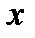 сгруппированы в одной точке, то есть в этом случае имеем функциональную зависимость.
сгруппированы в одной точке, то есть в этом случае имеем функциональную зависимость.
Пусть  весь разброс определяется внутригрупповой дисперсией. Это значит, что у нас нет зависимости (при изменении
весь разброс определяется внутригрупповой дисперсией. Это значит, что у нас нет зависимости (при изменении 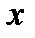 условные средние по
условные средние по  не меняются).
не меняются).
В качестве меры нелинейной связанности рассмотрим предложенную К. Пирсоном величину – корреляционное отношение.

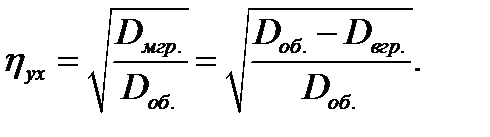
Она называется корреляционным отношением 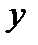 на
на 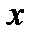 ,может быть записана еще так:
,может быть записана еще так:
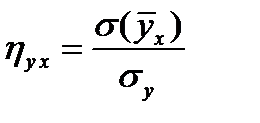
и представляет отношение среднего квадратичного отклонения условных средних 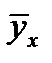 к полному среднему квадратичному отклонению
к полному среднему квадратичному отклонению 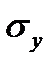 .
.
Свойства корреляционного отношения.
1. Всегда

2. Если между  и
и  нет корреляционной связи, то
нет корреляционной связи, то 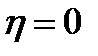 , а если
, а если  связано с
связано с 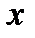 однозначной функциональной связью, то
однозначной функциональной связью, то 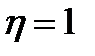 .
.
3. Всегда
 , то есть корреляционное отношение не меньше коэффициента корреляции.
, то есть корреляционное отношение не меньше коэффициента корреляции.
4. Условие, необходимое и достаточное для того, чтобы регрессия была линейной, заключается в выполнении равенства:
 , где
, где  - коэффициент корреляции.
- коэффициент корреляции.
То есть корреляционное отношение является мерой корреляционной связи  с
с  и, притом, какой угодно по форме. В последнем обстоятельстве заключается большое преимущество корреляционного отношения перед коэффициентом корреляции, который служит лишь мерой линейной корреляционной связи.
и, притом, какой угодно по форме. В последнем обстоятельстве заключается большое преимущество корреляционного отношения перед коэффициентом корреляции, который служит лишь мерой линейной корреляционной связи.
Можно проверить статистическую гипотезу о значимости корреляционного отношения то есть, рассмотреть вопрос 
Для этого выдвигают гипотезу вида:
 .
.
Для проверки гипoтезы рассмотрим случайную величину  , которая распределена по закону Стьюдента. Если
, которая распределена по закону Стьюдента. Если 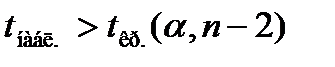 , то отвергаем «нулевую гипотезу»
, то отвергаем «нулевую гипотезу» 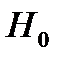 . Здесь
. Здесь  – уровень значимости (
– уровень значимости (  а
а  — число степеней свободы.
— число степеней свободы.  смотрим по таблице распределения Стьюдента.
смотрим по таблице распределения Стьюдента.
Корреляционное отношение и коэффициент корреляции для данного распределения могут отличаться друг от друга незначительно и тогда возникает вопрос, существенно ли их расхождение? Когда оно не существенно, тогда можно считать, что мы имеем дело с линейной регрессией  на
на  . Для оценки расхождения
. Для оценки расхождения  и
и  английский статистик Блэкман предложил рассматривать разность:
английский статистик Блэкман предложил рассматривать разность:
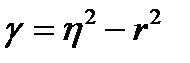 ,
,
и ее среднее квадратичное отклонение.
Выборочная ошибка этого показателя определяется по формуле:
 .
.
Критерием достоверности показателя  служит его отношение к своей ошибке
служит его отношение к своей ошибке 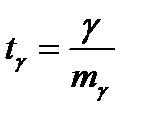 .
.
Для проверки критерия используют распределение Стьюдента.
Если  связь линейная.
связь линейная.
Если  связь нелинейная.
связь нелинейная.
Пример: Рассмотрим данные о живом весе  самок павианов гамадрилов в том возрасте
самок павианов гамадрилов в том возрасте  , когда у них наступает первый половой цикл, внешне выраженный набуханием половой кожи.
, когда у них наступает первый половой цикл, внешне выраженный набуханием половой кожи.
| Возраст X (мес.) | Вес Y (кг.) |
| 33.0 | 7.5 |
| 31.0 | 5.7 |
| 31.0 | 5.4 |
| 32.0 | 5.8 |
| 34.0 | 6.8 |
| 26.0 | 6.2 |
| 29.8 | 8.0 |
| 31.0 | 6.1 |
| 32.5 | 6.8 |
| 32.5 | 5.6 |
| 24.0 | 5.0 |
| 28.5 | 5.0 |
| 26.0 | 5.4 |
| 28.5 | 6.7 |
| 32.0 | 5.3 |
| 31.5 | 5.5 |
| 32.5 | 6.4 |
| 34.0 | 6.3 |
| 33.5 | 5.5 |
| 33.5 | 6.0 |
Найти корреляционное отношение  , проверить на зависимость и на линейность.
, проверить на зависимость и на линейность.
Решение: 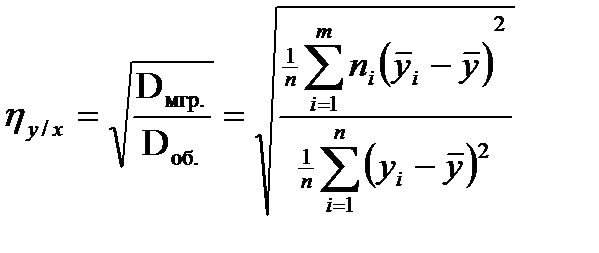 .
.

Пусть  ;
;
Так как  нулевую гипотезу отвергаем, то есть
нулевую гипотезу отвергаем, то есть  .
.
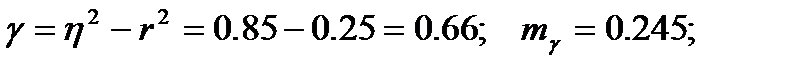
 Пусть
Пусть  зависимость не прямолинейная.
зависимость не прямолинейная.
|
из
5.00
|
Обсуждение в статье: Элементы корреляционного анализа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

