Распределения, связанные с нормальным законом распределения и используемые в математической статистике

 

Нормальный закон распределения (распределение Гаусса - Лапласа)

 

 

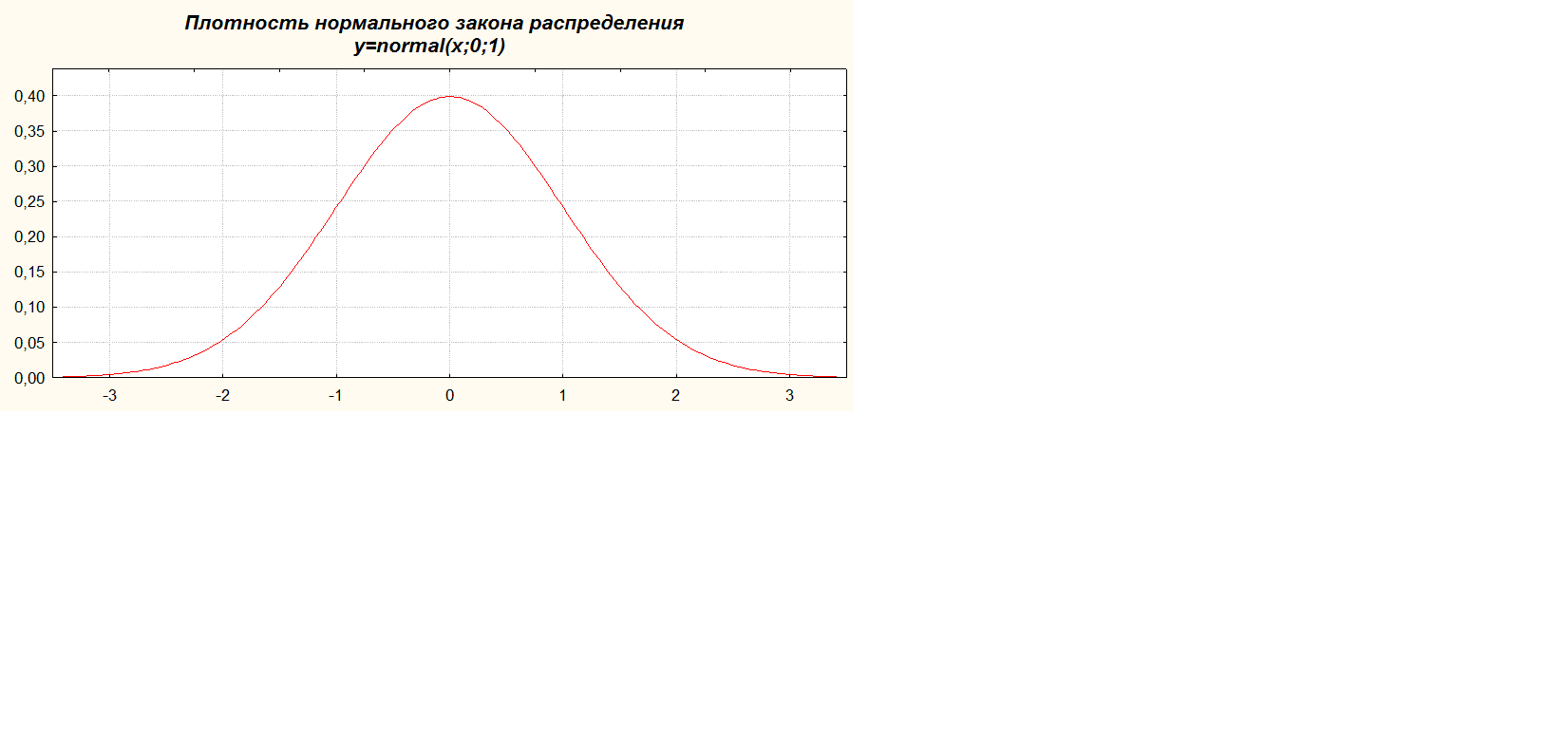
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

 

.

 

Нормальный закон полностью определяется двумя параметрами – .

Математическое ожидание – , стандартное отклонение – .

Если ввести преобразование вида: 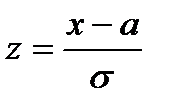, то случайная величина будет распределена по нормальному закону с параметрами (0, 1) (стандартное нормальное распределение).

Медиана , мода . Асимметрия . Эксцесс .

Точками перегиба функции плотности являются точки .

 

 

Распределение хи-квадратПирсона

 

 

 

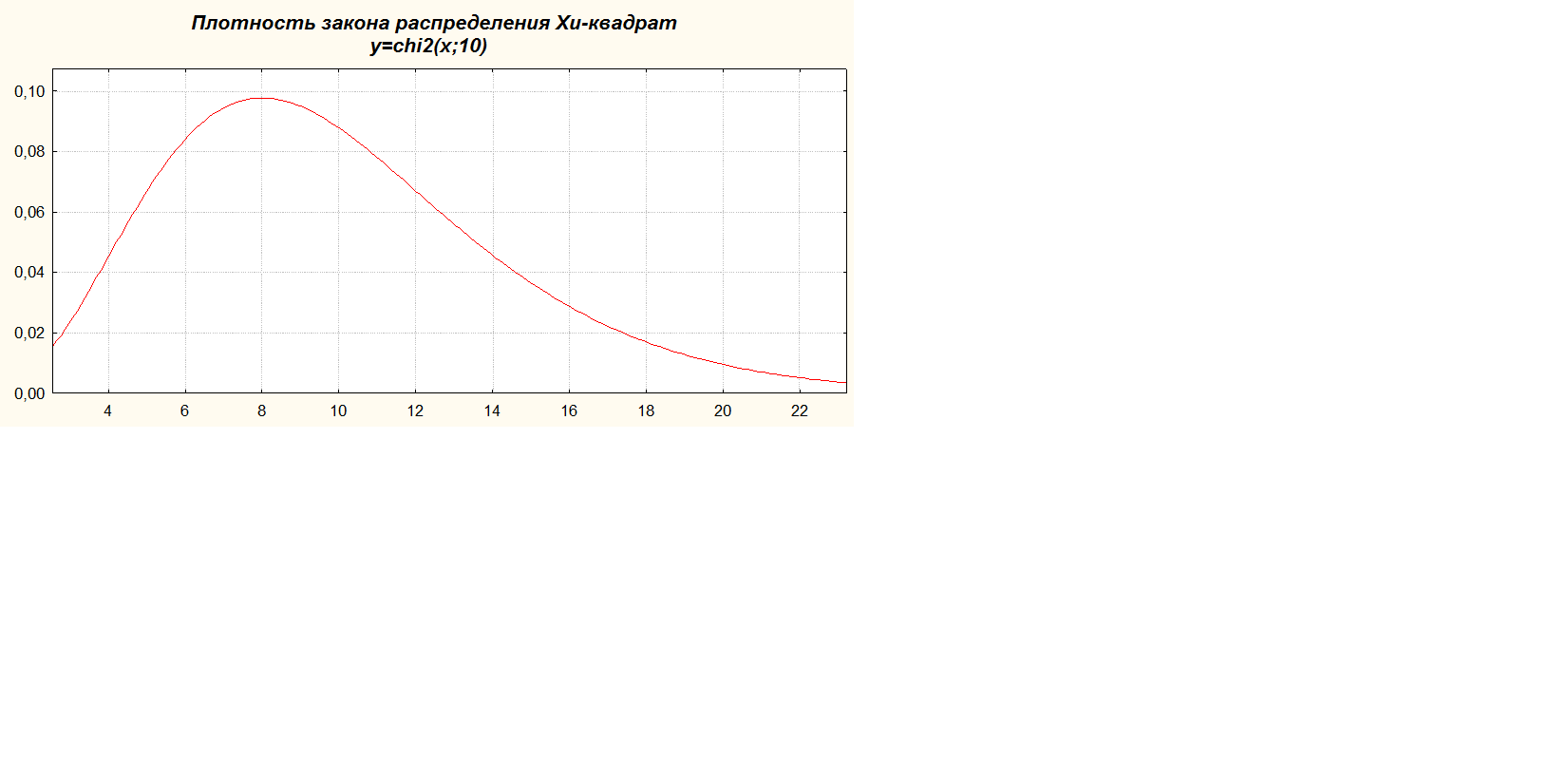
Распределение хи-квадрат является частным случаем семейства гамма-распределений. Распределение называют распределением хи-квадрат с степенями свободы и обозначают χ² (n).

Плотность закона распределения χ² (n):

С другой стороны χ² (n)= 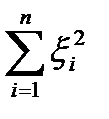, где – случайные величины, распределенные по нормальному закону распределения с параметрами .

Математическое ожидание . Медиана . Мода . Дисперсия . Асимметрия . Эксцесс .

Точками перегиба функции плотности являются точки (при условии, что x–действительное положительное число).

При случайная величина сходится к стандартному нормальному распределению.

 

Распределение Стьюдента

 

 

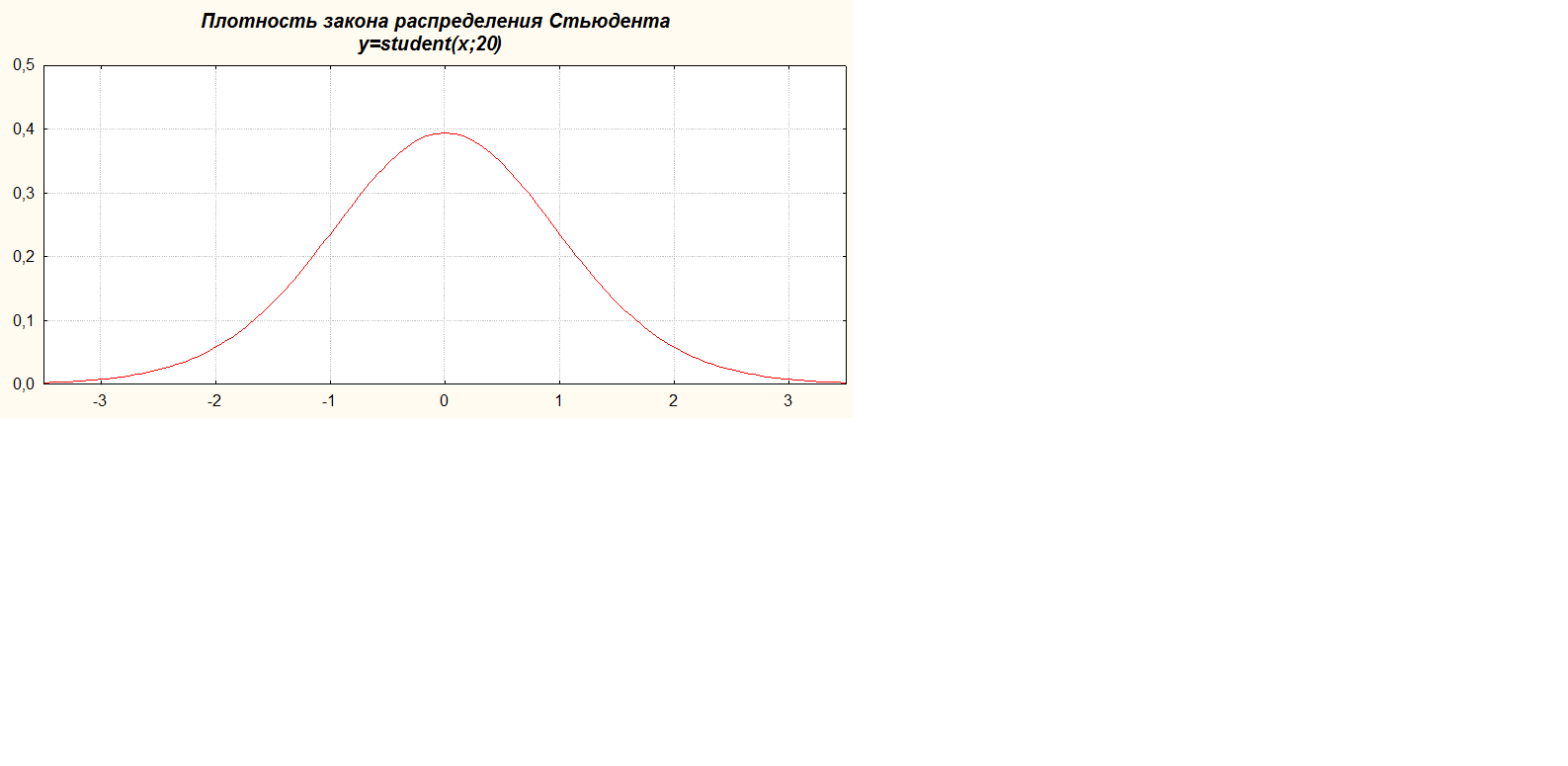
Случайной величиной, подчиняющейся распределению Стьюдента с n степенями свободы, называется отношение независимых случайных величин

,

где – случайная величина, распределенная нормально с параметрами (0, 1), а подчиняется распределению хи-квадрат с nстепенями свободы. В математической статистике распределение Стьюдента называют еще t – распределением.

Плотность закона распределения Стьюдента выражается формулой:

 

 

Замечание: При n=1 получаем функцию распределения Коши.

 

Математическое ожидание . Медиана . Мода . Дисперсия 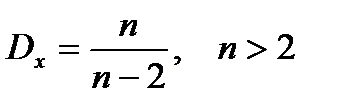. Асимметрия 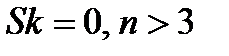. Эксцесс .

При 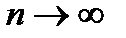(реально уже при n>30)распределение Стьюдента сходится к нормальному распределению с параметрами (0, 1).

 

Распределение Фишера – Снедекора

 

 

Рассмотрим случайные величины и отношение вида:

 

 

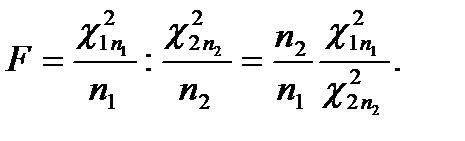
Распределение случайной величины Fназывают распределением Фишера – Снедекорас степенями свободы. Иногда это распределение называют F – распределением или распределением дисперсионного отношения Фишера.

 

Плотность распределения Фишера – Снедекора:

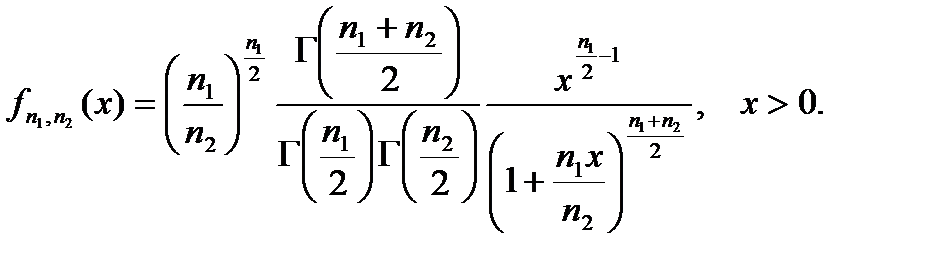
Математическое ожидание 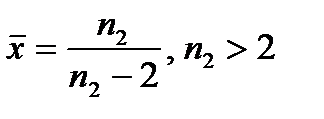. Мода . Дисперсия .

 

Статистические оценки

Рассмотрим произвольную статистическую модель F= соответствующую схеме повторных независимых наблюдений над некоторой случайной величиной . Таким образом, априорная информация о наблюдаемой случайной величине состоит в том, что известна ее функция распределения, а неизвестный (оцениваемый) параметр является элементом параметрического множества .

Теория статистического оценивания параметров законов распределения делится на две части:

1. Точечное оценивание.
2. Интервальное оценивание.

 

Точечное оценивание

 

Точечной называют оценку, которая определяется одним числом.

При точечном оценивание ищут статистику, значение которой при заданной реализации выборки принимают за приближенное значение параметра .

Требования, предъявляемые обычно к статистическим оценкам:

1. Несмещенность.
2. Эффективность.
3. Состоятельность.

 

Статистическую оценку называют несмещенной, если ее математическое ожидание равно оцениваемому параметру : .

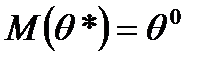Статистическую оценку называют эффективной, если (при заданном объеме выборки) она имеет наименьшую возможную дисперсию.

Статистическую оценку называют состоятельной, если при ее значение сходится по вероятности к оцениваемому параметру.

 

Иногда вводят понятие оптимальной оценки и достаточной статистики.

Несмещенную оценку с равномерно минимальной дисперсией называют оптимальной.

Статистика называется достаточной для модели F= если условная плотность (или вероятность в дискретном случае) 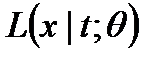случайного вектора при условии не зависит от параметра .

Это свойство статистики Tозначает, что она содержит всю информацию о параметре , имеющуюся в выборке и поэтому все заключения об этом параметре, которые можно сделать при наблюдении x, зависят только от .Или, иначе, все статистические выводы о модели, обладающей достаточной статистикой, формулируются в терминах этой достаточной статистики. Достаточная статистика, таким образом, дает оптимальный способ представления статистических данных.

 

Роль достаточных статистик в теории оценивании показывает следующее утверждение.

 

Теорема (Рао – Блекуэлл – Колмогоров): Оптимальная оценка, если она существует, является функцией от достаточной статистики.

 

Основными методами для получения точечной оценки параметров законов распределения являются:

1. Метод моментов.
2. Метод максимального (наибольшего) правдоподобия.