 |
Главная |
Построение линейных регрессионных моделей. Оценка параметров модели линейной регрессии с помощью метода наименьших квадратов (МНК)
|
из
5.00
|
Используемые обозначения:
| Y | — | зависимая (эндогенная) переменная; |
| X1, X2, …,Xk | — | объясняющие (экзогенные, независимые) переменные, регрессоры; |
| Х | — | матрица объясняющих переменныхразмерностью 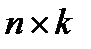 ,k - количество объясняющих факторов, n-количество наблюдений. ,k - количество объясняющих факторов, n-количество наблюдений.
|
| ХТ | — | транспонированная матрица объясняющих переменных; |
| εi | — | случайная составляющая; |
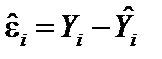
| — | ошибка, разница между фактическими и предсказанными по модели значениями эндогенной переменной, остаток[6]; |
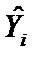
| — | предсказанное по модели значение Y, прогноз, прогнозное значение. |
Регрессионный анализпредназначен для исследования зависимости исследуемой переменной от различных факторов и отображения их взаимосвязи в форме регрессионной модели.
Спецификация регрессионной модели имеет следующую структуру
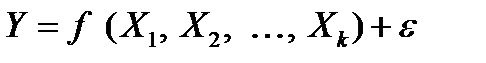 , (1.5)
, (1.5)
где Y — эндогенная (зависимая) переменная,X1, X2, …, Xk — независимые (экзогенные, объясняющие) переменные, или факторы, 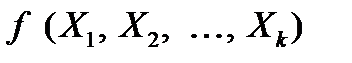 —детерминированная составляющая эндогенной переменной (уравнение регрессии), полностью объясняемая значением экзогенной переменной,e — случайная составляющая эндогенной переменной (случайное возмущение), которая не может быть объяснена значениями X1, X2, …, Xk.
—детерминированная составляющая эндогенной переменной (уравнение регрессии), полностью объясняемая значением экзогенной переменной,e — случайная составляющая эндогенной переменной (случайное возмущение), которая не может быть объяснена значениями X1, X2, …, Xk.
Зависимость между экономическими переменными типа (1.5) называется регрессионной зависимостью, эконометрические модели со спецификацией вида (1.5) — регрессионными моделями.
В то время как зависимая переменная должна быть непрерывной (за исключением логистической регрессии), независимые переменные могут быть как прерывными, так и категориальными, то есть как «пол» или «тип применяемого препарата».
Если между эндогенной переменной Y и 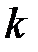 регрессорами существует линейная регрессионная зависимость, то (1.5) можно записать
регрессорами существует линейная регрессионная зависимость, то (1.5) можно записать
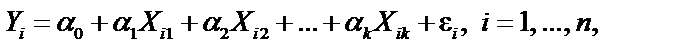 (1.6) (1.6)
|
где n — количество наблюдений;
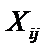 — i-ое наблюдение j – ой переменной,
— i-ое наблюдение j – ой переменной, 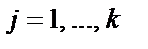 ;
;
k— количество факторов, включенных в модель.
Коэффициент уравнения регрессии 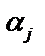 показывает на сколько единиц в среднем изменится зависимая переменная, если фактор Xj изменится на одну единицу при фиксированных значениях других факторов.
показывает на сколько единиц в среднем изменится зависимая переменная, если фактор Xj изменится на одну единицу при фиксированных значениях других факторов.
Оценка параметров модели выполняется методом наименьших квадратов (МНК). МНК минимизирует сумму квадратов отклонения наблюдаемых значений 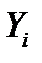 от предсказанных по модели значений
от предсказанных по модели значений 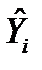 .
.
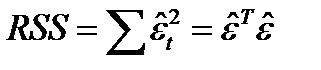 ®min, (1.7)
®min, (1.7)
Предположим, что для оценки линейной регрессии взята выборка, состоящая из n пар значений переменных (Xi, Yi), где i = 1, 2, …, n. Тогда f(x) можно представить в виде:
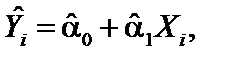
| (1.8) |
где 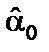 и
и 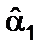 — параметры регрессии, которые должны быть определены по выборочным данным с помощьюметода наименьших квадратов (МНК).
— параметры регрессии, которые должны быть определены по выборочным данным с помощьюметода наименьших квадратов (МНК).
Согласно принципу метода наименьших квадратовоценки 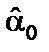 и
и 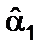 находятся путем минимизации суммы квадратов
находятся путем минимизации суммы квадратов
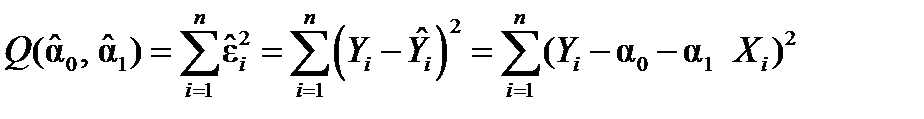
|
по всем возможным значениям 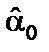 и
и 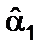 при заданных (наблюдаемых) значениях Xи Y.Задача сводится к математической задаче поиска точки минимума функции двух переменных. Точка минимума находится путем приравнивания нулю частных производныхфункции z = Q(α0, α1) по переменным
при заданных (наблюдаемых) значениях Xи Y.Задача сводится к математической задаче поиска точки минимума функции двух переменных. Точка минимума находится путем приравнивания нулю частных производныхфункции z = Q(α0, α1) по переменным 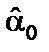 и
и 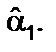
Это приводит к системе нормальных уравнений
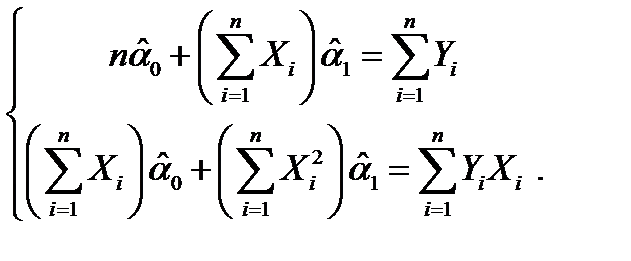
Решая которую находят оценки параметров:
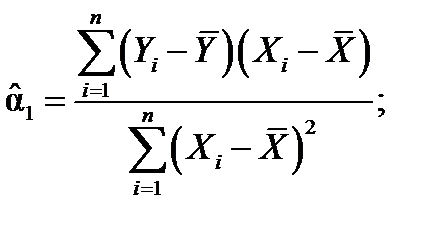 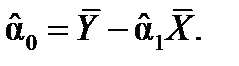
| (1.9) |
Оценки 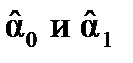 называют оценками наименьших квадратов. Используя формулы для вычисления выборочной дисперсии и коэффициента парной корреляции (формулы 1.1—1.2), параметр
называют оценками наименьших квадратов. Используя формулы для вычисления выборочной дисперсии и коэффициента парной корреляции (формулы 1.1—1.2), параметр 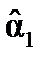 можно получить следующим образом:
можно получить следующим образом:
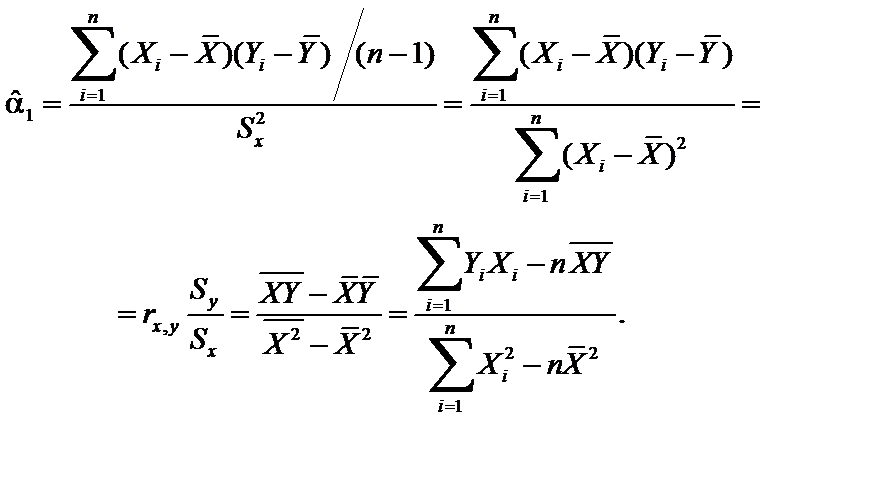
| (1.10) |
Формулу для вычисления параметров модели множественной регрессии приведем без вывода
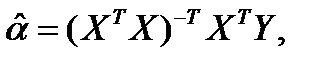
| (1.11) |
где
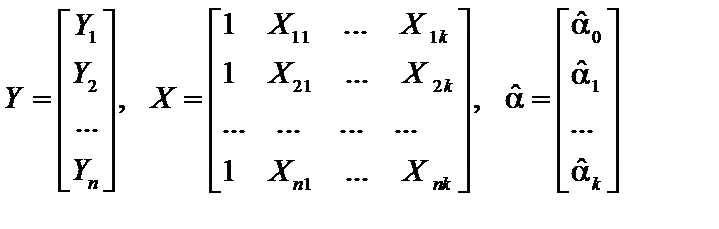 .
.
Оценив по выборочным данным 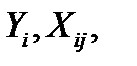
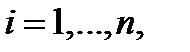
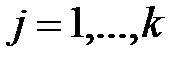 ,вектор параметров
,вектор параметров 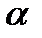 , можно вычислить оценку вектора значений эндогенной переменной
, можно вычислить оценку вектора значений эндогенной переменной
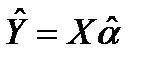 . (1.12)
. (1.12)
Пример 1.2. Оценка параметров модели парной регрессии
Оценить параметры модели парной регрессии с помощью:
а) надстройки Анализ данных, используя инструмент Регрессия;
б) с помощью функции ЛИНЕЙН;
в) с помощью матричных функций Excel по формуле 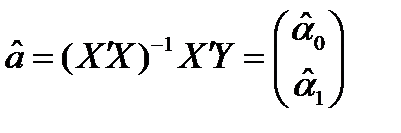 ;
;
г) с помощью надстройки Excel Поиск решения;
д) по формулам: 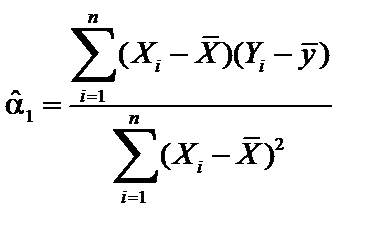 ,
, 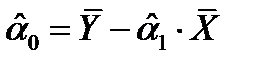 .
.
Выпишите полученное уравнение регрессии. Дайте экономическую интерпретацию параметрам модели регрессии индекса реального ВВП РФ на индекс реальных инвестиций в основной капитал. Отобразите на графике исходные данные и результаты моделирования.
|
из
5.00
|
Обсуждение в статье: Построение линейных регрессионных моделей. Оценка параметров модели линейной регрессии с помощью метода наименьших квадратов (МНК) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

