Математическая модель поверхностей

Поверхности, как и линии, являются математическими абстракциями, дающие представление об отдельных свойствах предметов. Так же, как и кривые линии, поверхности будут служить нам строительным материалом для создания тел. В свою очередь, поверхности мы будем описывать с помощью скалярных величин, векторов, линий и других поверхностей. В данной главе мы рассмотрим способы построения различных поверхностей.

Пусть в пространстве задана некоторая глобальная декартова прямоугольная система координат с базисными векторами Мы будем представлять поверхность векторной функцией

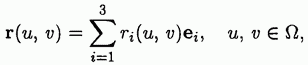(3.1.1)

двух скалярных аргументов u и v. Будем считать, что компоненты радиус-вектора точки поверхности являются однозначными непрерывными функциями параметров . Такое описание поверхностей называется параметрическим.

Область изменения параметров поверхности О в общем случае представляет собой произвольную связную двухмерную область на плоскости , ограниченную двухмерными контурами Параметры поверхности являются координатами некоторой двухмерной точки на параметрической плоскости, принадлежащей области П.

Рис. 3.1.1. Область определения поверхности П на плоскости параметров

Область определения параметров поверхности имеет внешнюю границу и может иметь вырезы внутри, но она должна быть связной, так чтобы из каждой точки области можно было попасть в любую другую точку, не пересекая границы области.

В частном случае область определения параметров поверхности может представлять собой прямоугольник, когда параметры принимают значения в пределах Прямоугольные области определения параметров удобны для практического применения и часто используются, так как их математическая модель достаточно проста. Прямоугольные области определения параметров имеют исходные или базовые поверхности, которые служат заготовками для более сложных поверхностей. Пример области параметров поверхности приведен на рис. 3.1.1.

Поверхности могут быть замкнутыми или разомкнутыми. Замкнутые поверхности будут иметь прямоугольные области определения параметров. Для замкнутой по -линии поверхности ; для замкнутой по -линии поверхности Поверхность может быть замкнута по обеим координатным линиям.

Некоторые поверхности можно описать с помощью уравнения , которому удовлетворяют компоненты радиус-вектора ее точек. Такое описание поверхности называется неявным. В обыкновенной точке уравнение поверхности можно переписать в виде, разрешенном относительно одной из координат, например . Неявное описание поверхности в отличие от параметрического описания не всегда однозначно, что вызывает определенные трудности. Кроме того, при переходе в другую систему координат описывающее поверхность уравнение изменяется. Для моделирования поверхностей мы будем использовать их параметрическое представление.

Математическая модель поверхности включает в себя функциональную зависимость радиус-вектора r(u,v) от параметров и двухмерную область О изменения параметров и и v. Таким образом, математическая модель поверхности в общем случае должна содержать и математическую модель области определения своих параметров.

Общение с математической моделью поверхности происходит аналогично общению с кривой. Мы обращаемся к функциям поверхности с некоторыми значениями двух ее параметров и в качестве ответа получаем геометрическую информацию о поверхности в точке, соответствующей данным значениям параметров. Если некоторая функция поверхности допускает выход значений параметров за область определения, то данная функция должна выдавать геометрическую информацию для продолжения поверхности.

Аналитические поверхности. Каждая такая поверхность определяется одним математическим уравнением с неизвестными X, Y и Z (эти неизвестные обозначают искомые координаты поверхности). Иначе говоря, чтобы изобразить любую аналитическую поверхность, необходимо знать математическое уравнение, которым она описывается. На Рис. 6.5 представлена поверхность, описываемая уравнением .

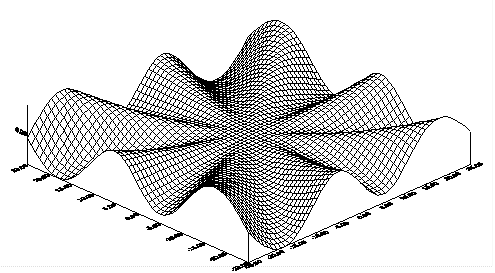
Рис. 6.5 – Аналитически заданная поверхность.

Аналитические поверхности широко используются в технике. Например, отражатель фары или прожектора должен иметь точную форму параболоида вращения, а ряд ферменных конструкций состоят из гиперболоидов вращения. Гиперболоид удобен тем, что его можно получить соединением прямолинейных стержней. На основе гиперболоидов инженером В.Г. Шуховым в 1922г. была построена знаменитая башня на ул. Шаболовка в Москве (Рис. 6.6).

14. Способы построения поверхностей. Поверхности на базе линий.

Линии соединяющие точки, они же ребра

Соединение вершин, рёбер по сути это и сеть построение поверхностей.

Можно например екструдировать ребро и получится грань (полигон)

15. Полигональное моделирования. Основные элементы полигонального моделирования.