 |
Главная |
Вычисление обратной матрицы
|
из
5.00
|
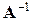 =
= 

где  =
=  - определитель матрицы
- определитель матрицы 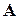
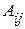 - алгебраические дополнения элементов
- алгебраические дополнения элементов 
Пример. Вычислить матрицу 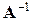 , обратную матрице
, обратную матрице 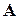
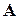 =
= 
 =
=  =
= 

 = 30;
= 30;
 =
= 
 =
= 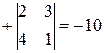 ;
;  =
= 
 =
=  ;
;
 =
= 
 =
= 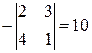 ;
; 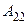 =
= 
 =
=  ;
;
 =
= 
 =
= 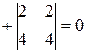 ;
;  =
= 
 =
=  ;
;
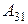 =
= 
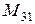 =
=  ;
;
 =
= 
 =
=  ;
; 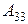 =
= 
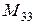 =
=  ;
;
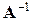 =
=  =
= 
 =
= 
 =
= 
Проверка  =
= 

 =
= 
Линейным уравнением называется уравнение вида
 где
где  и b – числа,
и b – числа,  - неизвестные.
- неизвестные.
Таким образом, в левой части линейного уравнения стоит линейная комбинация неизвестных, а в правой – число.
Линейное уравнение называется однородным, если b = 0. В противном случае уравнение называется неоднородным.Системой линейных уравнений (линейной системой) называется система вида
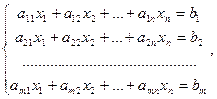
где  ,
, 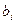 - числа,
- числа,  - неизвестные, n – число неизвестных, m – число уравнений.
- неизвестные, n – число неизвестных, m – число уравнений.
Решением линейной системы называется набор чисел  которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.
которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.
Метод Гаусса решения линейных систем.
Линейная система может иметь единственное решение, бесконечно много решений или не иметь ни одного решения.
Дана система линейных уравнений: 
Пусть 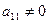 (этого всегда можно добиться, поменяв уравнения местами). Разделим обе части первого уравнения на
(этого всегда можно добиться, поменяв уравнения местами). Разделим обе части первого уравнения на  и вычтем полученное уравнение из каждого из остальных уравнений системы, умножив его предварительно на
и вычтем полученное уравнение из каждого из остальных уравнений системы, умножив его предварительно на  где i – номер очередного уравнения. Коэффициенты при
где i – номер очередного уравнения. Коэффициенты при  во всех уравнениях этой системы, начиная со второго, будут равны 0, т.е. система выглядит так:
во всех уравнениях этой системы, начиная со второго, будут равны 0, т.е. система выглядит так:
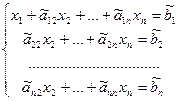 .
.
Если новые коэффициенты при х2 не все равны нулю, можнотаким же образом исключить 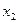 из третьего и последующих уравнений. Продолжая эту операцию для следующих неизвестных, приведем систему к так называемому треугольному виду:
из третьего и последующих уравнений. Продолжая эту операцию для следующих неизвестных, приведем систему к так называемому треугольному виду:
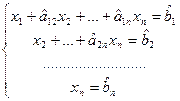 .
.
Здесь символами  и
и  обозначены изменившиеся в результате преобразований числовые коэффициенты и свободные члены.
обозначены изменившиеся в результате преобразований числовые коэффициенты и свободные члены.
Из последнего уравнения системы единственным образом определяется  , а затем последовательной подстановкой – остальные неизвестные.
, а затем последовательной подстановкой – остальные неизвестные.
Иногда в результате преобразований в каком-либо из уравнений обращаются в 0 все коэффициенты и правая часть, то есть уравнение превращается в тождество 0=0. Исключив его из системы, мы уменьшим число уравнений по сравнению с числом неизвестных. Такая система не может иметь единственного решения.
Если же в процессе применения метода Гаусса какое-нибудь уравнение превратится в равенство вида 0=1 (коэффициенты при неизвестных обратились в 0, а правая часть приняла ненулевое значение), то исходная система не имеет решения, так как подобное равенство является неверным при любых значениях неизвестных.
Правило Крамера.
Рассмотрим систему линейных уравнений. Назовем главным определителем этой системы определитель  , элементами которого являются коэффициенты при неизвестных:
, элементами которого являются коэффициенты при неизвестных: 
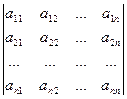 .
.
Правило Крамера позволяет найти единственное решение системы или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:
1) Если 
 система (2.3) имеет единственное решение, определяемое по формулам:
система (2.3) имеет единственное решение, определяемое по формулам: 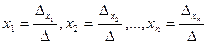 .
.
2) Если  =
=  =0, система имеет бесконечно много решений.
=0, система имеет бесконечно много решений.
3) Если  =0, а хотя бы один из
=0, а хотя бы один из 
 система не имеет решений.
система не имеет решений.
Линейная система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная линейная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Пример. Решить систему уравнений с помощью формул Крамера.

Решение. 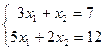 .
.
Обозначим  ,
,  ,
,  .
.
Найдем определитель системы  , по теореме Крамера система имеет единственное решение.
, по теореме Крамера система имеет единственное решение.
Вычислим определители:  ;
; 
 .
.
Теперь по формулам Крамера получаем:
 ;
; 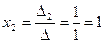 , т.е. решение системы
, т.е. решение системы  .
.
Вопросы для самопроверки.
1. Как характеризуется вектор в n-мерной прямоугольной системе координат?
2. Чему равно скалярное произведение двух векторов?
3. Как определяется местоположение элемента в матрице?
4. Что такое единичная матрица?
5. Что такое транспонированная матрица?
6. Каким требованиям должны удовлетворять перемножаемые матрицы?
7. Что такое обратная матрица?
8. Как находить решение системы линейных алгебраических уравнений с помощью формулы Крамера?
9. Как находить решение системы линейных алгебраических уравнений методом Гаусса?
ТЕМА 2. ФУНКЦИИ.
|
из
5.00
|
Обсуждение в статье: Вычисление обратной матрицы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

