|
Главная |
Понятие функции многих переменных. Частные производные.
|
из
5.00
|
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Пусть имеется n+1 переменных x1, x2, ..., xn, y, которые связаны между собой так, что каждому набору числовых значений переменных x1, x2, ..., xn соответствует единственное значение переменной y. Тогда говорят, что задана функция f от n переменных. Число y, поставленное в соответствие набору x1, x2, ..., xn называется значением функции f в точке (x1, x2, ..., xn), что записывается в виде формулы y = f(x1,x2,..., xn) или y =y(x1,x2,..., xn).Переменные x1, x2, ..., xn являются аргументами этой функции, а переменная y ‑ функцией от n переменных.
Далее будем говорить лишь о функции двух переменных. Для функций большего числа переменных все факты, о которых будет идти речь, или аналогичны или сохраняются без всякого изменения. Аргументы функции двух переменных будем обозначать, как правило x и y, а значение функции z.
|
|
Будем говорить, что задана функция двух переменных, если любой паре чисел (x,y) из некоторого множества D упорядоченных пар чисел поставлено в соответствие единственное число, которое обозначается f(x,y) и называется значением функции f в точке (x,y).
Множество D называется областью определения функции.
Поскольку любую пару чисел x,y можно рассматривать как пару координат точки M на плоскости, вместо z=f(x,y) можно писать z=f(M).При этом аргументами функции будут координаты x,y точки M.
Числа x,y можно рассматривать как координаты вектора  , исходящего из начала координат и с концом в точке M(x,y). Тогда функция двух переменных будет функцией вектора, что записывается в виде формулы z = f(
, исходящего из начала координат и с концом в точке M(x,y). Тогда функция двух переменных будет функцией вектора, что записывается в виде формулы z = f(  ), причем аргументами функции являются координаты вектора
), причем аргументами функции являются координаты вектора  .
.
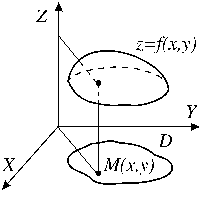
График функции двух переменных есть множество точек (x,y,f(x,y)), где (x,y)ÎD. График представляет собой некоторую поверхность. Пример такой поверхности приводится на рисунке.
|
|
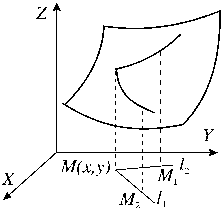
Очевидно, что нельзя ввести понятия возрастания или убывания (монотонности) функции двух переменных. Рассмотрим график некоторой функции z=f(x,y), изображенный на рисунке . Из точки M(x,y) в плоскости X,Y проведем два луча l1 и l2 , определяющих некоторые направления. Можно говорить, что в точке M функция f в направлении l1 возрастает, а в направлении l2 убывает. Это означает, что для любой точки M1 , лежащей на луче l1 достаточно близко к точке M, выполняется неравенство f(M1) > f(M). Для любой точки M2 , лежащей на луче l2 достаточно близко к точке M, выполняется неравенство f(M2) < f(M).
Частной производной по x функции z = f(x,y) в точке M0(x0,y0) называется предел 
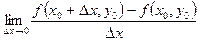 , если этот предел существует. Обозначается эта частная производная любым из следующих символов:
, если этот предел существует. Обозначается эта частная производная любым из следующих символов: 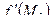 ;
; 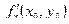 ;
; 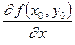 .
.
Частная производная по x есть обычная производная от функции z = f(x,y), рассматриваемой как функция только от переменной x при фиксированном значении переменной y.
Совершенно аналогично можно определить частную производную по y функции z = f(x,y) в точке M0(x0,y0): 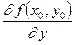 =
= 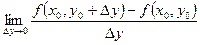 .
.
Примеры.
1.  .
.
2. 
Если частные производные функции z = f(x,y) существуют на некотором множестве, а точка, в которой вычисляются частные производные, несущественна, то пользуются более короткими обозначениями: 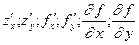 .
.
Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные производные по x и по y. Они называются вторыми частными производными или частными производными второго порядка и обозначаются zxx¢¢, zyy ¢¢ , zxy ¢¢ или 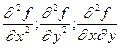 . Согласно определению
. Согласно определению 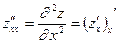 ;
; 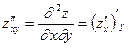 . Последняя частная производная второго порядка называется смешанной. Смешанная частная производная второго порядка, вообще говоря, зависит от того, в какой последовательности берутся переменные, по которым вычисляется производная. Так, производная zxy ¢¢ = (zx ¢ )y ¢ может не быть равной zyx ¢¢ = (zy ¢ )x ¢. Однако существует теорема, утверждающая, что если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности вычислялись частные производные по x и по y.
. Последняя частная производная второго порядка называется смешанной. Смешанная частная производная второго порядка, вообще говоря, зависит от того, в какой последовательности берутся переменные, по которым вычисляется производная. Так, производная zxy ¢¢ = (zx ¢ )y ¢ может не быть равной zyx ¢¢ = (zy ¢ )x ¢. Однако существует теорема, утверждающая, что если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности вычислялись частные производные по x и по y.
Вопросы для самопроверки.
1. Как определяется функция двух переменных?
2. Что такое частная производная?
КОНТРОЛЬНЫЕ ЗАДАНИЯ.
Задача 1.
Найти сумму, разность, произведение и частное в алгебраической форме для комплексных чисел 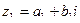 и
и 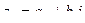 .
.
| вариант | 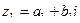 
| 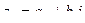
|
| 1 | 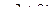
| 
|
| 2 | 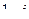
| 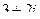
|
| 3 | 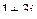
| 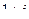
|
| 4 | 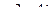
| 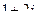
|
| 5 | 
| 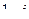
|
| 6 | 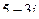
| 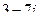
|
| 7 | 
| 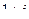
|
| 8 | 
| 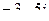
|
| 9 | 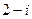
| 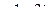
|
| 10 | 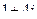
| 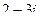
|
Задача 2.
Систему решить методом Гаусса и с помощью формул Крамера.
| Вариант | Система уравнений | Вариант | Система уравнений |
| 1 | 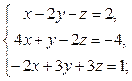
| 6 | 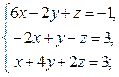
|
| 2 | 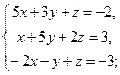
| 7 | 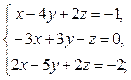
|
| 3 | 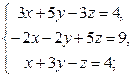
| 8 | 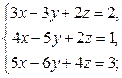
|
| 4 | 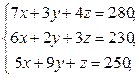
| 9 | 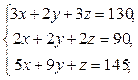
|
| 5 | 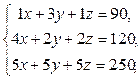
| 10 | 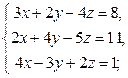
|
Задача 3.
Найти область определения функции
| вариант | функция | вариант | функция |
| 1 | 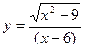
| 6 | 
|
| 2 | 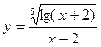
| 7 | 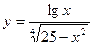
|
| 3 | 
| 8 | 
|
| 4 | 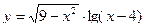
| 9 | 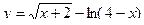
|
| 5 | 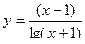
| 10 | 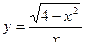
|
Задача 4.
Вычислить пределы
| варианты | |
| 1 | 1) 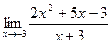 2) 2) 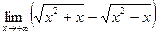 3) 3) 
|
| 2 | 1) 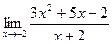 2) 2) 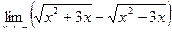 3) 3) 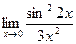
|
| 3 | 1)  2) 2) 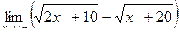 3) 3) 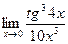
|
| 4 | 1) 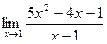 2) 2) 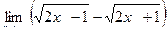 3) 3) 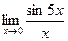
|
| 5 | 1) 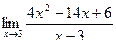 2) 2) 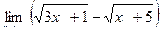 3) 3) 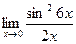
|
| 6 | 1)  2) 2)  3) 3) 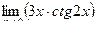
|
| 7 | 1) 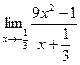 2) 2) 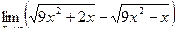 3) 3) 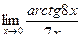
|
| 8 | 1) 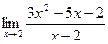 2) 2) 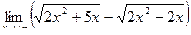 3) 3) 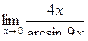
|
| 9 | 1) 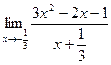 2) 2) 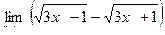 3) 3) 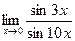
|
| 10 | 1) 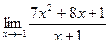 2) 2) 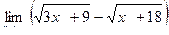 3) 3) 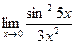
|
Задача 5.
Найти производную функции
| вариант | функции |
| 1 | а) y = 2sin x – x5; б) f(x) = x2•ех |
| 2 | а) y = sin x + ex; б) 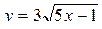
|
| 3 | а) у = х2 + х3– 4 б) у= 2sinx – 3 |
| 4 | а) 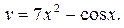 б) у= 4x + ex – 7 б) у= 4x + ex – 7
|
| 5 | а) 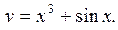 б) у = 2lnx + 5 б) у = 2lnx + 5
|
| 6 | а) 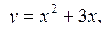 б) y = 6х + 3sin (2x); б) y = 6х + 3sin (2x);
|
| 7 | а) 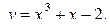 б) у = 3х+7sin x б) у = 3х+7sin x
|
| 8 | а)  б) y = 2x5 – 3cos x; б) y = 2x5 – 3cos x;
|
| 9 | а) у = 3x4 – sin x + 5; б) 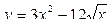
|
| 10 | а) у = ln x – 2cosx; б) y = х2 -3х |
Задача 6.
Составить уравнение касательной к данной кривой в точке с абсциссой 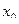
| вариант | Уравнение кривой | Абсцисса точки |
| 1 | 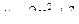
| 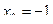
|
| 2 | 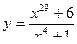
| 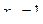
|
| 3 | 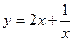
| 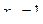
|
| 4 | 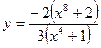
| 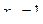
|
| 5 | 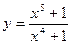
| 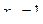
|
| 6 | 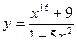
| 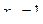
|
| 7 | 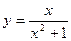
| 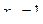
|
| 8 | 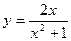
| 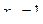
|
| 9 | 
| 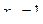
|
| 10 | 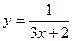
| 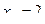
|
Задача 7.
Найти неопределенные интегралы, результат проверить дифференцированием.
| вариант | |
| 1 | 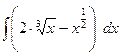
|
| 2 | 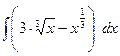
|
| 3 | 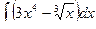
|
| 4 | 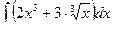
|
| 5 | 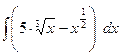
|
| 6 | 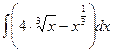
|
| 7 | 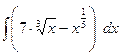
|
| 8 | 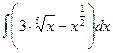
|
| 9 | 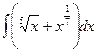
|
| 10 | 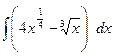
|
Задача 8.
Исследовать на сходимость ряд
| Вариант | Вариант | ||
| 1 | 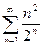
| 6 | 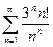
|
| 2 | 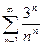
| 7 | 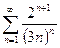
|
| 3 | 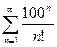
| 8 | 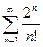
|
| 4 | 
| 9 | 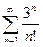
|
| 5 | 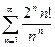
| 10 | 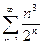
|
Задача 9.
Найти общее решение (или общий интеграл) дифференциального уравнения первого порядка.
| вариант | |
| 1 | 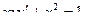
|
| 2 | 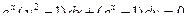
|
| 3 | 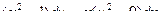
|
| 4 | 
|
| 5 | 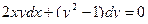
|
| 6 | 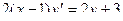
|
| 7 | 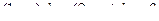
|
| 8 | 
|
| 9 | 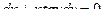
|
| 10 | 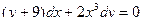
|
Задача 10.
Решить линейное дифференциальное уравнение.
| вариант | |
| 1 | 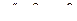
|
| 2 | 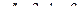
|
| 3 | 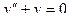
|
| 4 | 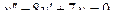
|
| 5 | 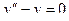
|
| 6 | 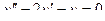
|
| 7 | 
|
| 8 | 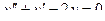
|
| 9 | 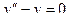
|
| 10 | 
|
Литература.
Основные источники:
1. Богомолов Н.В. Математика: учебник для ссузов. М: Дрофа, 2010-
395с.;
2. Богомолов Н.В. Сборник задач по математике: учебное пособие для ссузов. М: Дрофа, 2012-204с.;
Дополнительные источники:
1.Пехлецкий И.Д. Математика: учебник.- М: Форум,2009.
3. Жуков В.М. Практические занятия по математике : теория, задания , ответы -Ростов н/Д: Феникс, 2012.
4. Симонов А.Я., Бакаев Д.С., Эпельман А.Г. и др. Система тренировочных задач и упражнений по математике. - М: Просвещение, 1991.
5. Соловейчик И.Л., Лисичкин В.Т., Сборник задач по математике с
решениями для техникумов.-М.: ООО «Издательский дом «Оникс 21 век» ,
2003.
|
из
5.00
|
Обсуждение в статье: Понятие функции многих переменных. Частные производные. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы