 |
Главная |
Тема8. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
|
из
5.00
|
Понятие дифференциального уравнения. Частные и общие уравнения. Начальные условия. Уравнения первого порядка: с разделяющимися переменными, линейные уравнения. Линейные уравнения с постоянными коэффициентами. Характеристическое уравнение.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Дифференциальными уравнениями называются уравнения, в которых неизвестными являются функции одной или нескольких переменных, и в уравнения входят не только сами функции, но и их производные. Если производные, входящие в уравнение, берутся только по одной переменной, то дифференциальное уравнение называется обыкновенным. Если в уравнении встречаются производные по нескольким переменным, то уравнение называется уравнением в частных производных. Мы будем рассматривать лишь обыкновенные дифференциальные уравнения.
Начнем с дифференциальных уравнений первого порядка. Это уравнения, в которые входит лишь первая производная неизвестной функции. Это уравнение может быть записано в виде F(x,y,y¢) = 0.
Здесь x ‑ независимая переменная, y ‑ её неизвестная функция,  ‑ производная функции y, F ‑ заданная функция трех переменных. Функция F может быть задана не для всех значений её аргументов, поэтому можно говорить об области B определения функции F координатного пространства, то есть о множестве точек координатного пространства трех переменных x,y,y¢.
‑ производная функции y, F ‑ заданная функция трех переменных. Функция F может быть задана не для всех значений её аргументов, поэтому можно говорить об области B определения функции F координатного пространства, то есть о множестве точек координатного пространства трех переменных x,y,y¢.
Приведем примеры дифференциальных уравнений первого порядка:
y¢ – x4 = 0; xsiny¢ – lny = 0; xcosy + (y¢ – y2)sinx = 0.
Решением уравнения называется такая функция y = j(x), определенная на некотором промежутке (x1, x2), что при подстановке её вместо y в уравнение получается верное равенство на всем промежутке (x1, x2). Очевидно, что подстановка y = j(x) возможна только тогда, когда функция j(x) на промежутке (x1, x2) имеет первую производную. Необходимо также, чтобы при любом значении переменной x из промежутка (x1, x2) точка с координатами x, y, y¢ принадлежала множеству B, на котором определена функция F. Совокупность всех решенийдифференциального уравнения называется его общим решением.
В некоторых случаях уравнение F(x,y,y¢) = 0 определяет переменную y¢ как функцию независимых переменных x и y: y¢ = f(x,y). Процесс нахождения решения дифференциального уравнения называется его интегрированием. В результате интегрирования дифференциального уравнения первого порядка получают не одно решение, а семейство решений, зависящих от одной произвольной постоянной С:
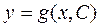
Если решение получено в виде, не разрешенном относительно у:

то его называют общим интегралом дифференциального уравнения 1-го порядка.
Всякое решение, получающееся из общего при конкретном числовом значении произвольной постоянной  называется частным решением:
называется частным решением:

Пример. Найти общее решение уравнения y = 3x.
Решение. Интегрируя, находим
y = 3x dx, y = 3x2/2 + C, где С - произвольная постоянная. Придавая С конкретные числовые значения, будем получать частные решения, например, y = 3x2/2 (С= 0), y = 3x2/2 + 5 (С = 5) и т.д.
Дифференциальное уравнение вида  называется дифференциальным уравнением с разделяющимися переменными. Отличительной особенностью уравнений этого типа является то, что в правой их части находится произведение функций
называется дифференциальным уравнением с разделяющимися переменными. Отличительной особенностью уравнений этого типа является то, что в правой их части находится произведение функций 
 одна из которых зависит только от x, другая только от y.
одна из которых зависит только от x, другая только от y.
Для того, чтобы найти решение такого уравнения, нужно разделить переменные x и y, собрав в левой и правой его частях функции, зависящие только от одной переменной.
Пример. Решить дифференциальное уравнение: 
Решение. Данное уравнение является уравнением с разделяющимися переменными. Заменим  на
на 
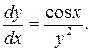 Разделим переменные, умножая обе части уравнения на
Разделим переменные, умножая обе части уравнения на 
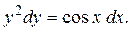 .
.
Интегрируя полученное равенство, получим:
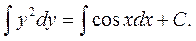
Отсюда  – общий интеграл данного уравнения. Разрешая его относительно у, можно записать общее решение данного уравнения в виде
– общий интеграл данного уравнения. Разрешая его относительно у, можно записать общее решение данного уравнения в виде

Ответ: 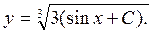
Дифференциальное уравнение вида  где
где  – заданные функции, называется линейным дифференциальным уравнением 1-го порядка. Отличительной особенностью линейного уравнения является то, что искомая функция y и ее первая производная
– заданные функции, называется линейным дифференциальным уравнением 1-го порядка. Отличительной особенностью линейного уравнения является то, что искомая функция y и ее первая производная  входят в уравнение в первых степенях и не перемножаются между собой, т.е. связаны линейно.Для решения уравнения воспользуемся способом подстановки. Будем искать неизвестную функцию y в виде произведения двух тоже пока неизвестных функций, т.е. положим
входят в уравнение в первых степенях и не перемножаются между собой, т.е. связаны линейно.Для решения уравнения воспользуемся способом подстановки. Будем искать неизвестную функцию y в виде произведения двух тоже пока неизвестных функций, т.е. положим 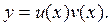 Тогда
Тогда  Подставив значения y и
Подставив значения y и  в уравнение (6), получим:
в уравнение (6), получим:  или
или  . Если выбрать
. Если выбрать  так, чтобы выражение, стоящее в скобках, обратилось в нуль, т.е.
так, чтобы выражение, стоящее в скобках, обратилось в нуль, т.е.  ,то вторая функция
,то вторая функция  должна удовлетворять уравнению
должна удовлетворять уравнению 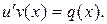
Пример.Решить уравнение  .
.
Решение. Решение этого уравнения будем искать в виде  , где
, где 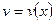 - некоторое решение уравнения
- некоторое решение уравнения  , а
, а  - решение уравнения
- решение уравнения  . Решим уравнение
. Решим уравнение  , это уравнение с разделяющимися переменными.
, это уравнение с разделяющимися переменными.  выполним почленное интегрирование:
выполним почленное интегрирование:  . Положим
. Положим  , тогда
, тогда 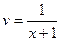 . Подставим найденную функцию в уравнение
. Подставим найденную функцию в уравнение  , получаем уравнение
, получаем уравнение  . Почленно интегрируя последнее равенство, получаем:
. Почленно интегрируя последнее равенство, получаем:  . Таким образом, решение исходного уравнения имеет вид:
. Таким образом, решение исходного уравнения имеет вид: 
Дифференциальное уравнение вида 
где n – действительное число,  , называется уравнением Бернулли. Уравнение Бернулли является обобщением линейного дифференциального уравнения и может быть решено тем же способом.
, называется уравнением Бернулли. Уравнение Бернулли является обобщением линейного дифференциального уравнения и может быть решено тем же способом.
Функция f ( x , y ) называется однороднойизмерения m, если

Дифференциальное уравнение вида P(x , y)dx + Q(x , y)dy = 0
называется однородным, если P(x , y) и Q(x , y) – однородные функции одного измерения.
Однородное дифференциальное уравнение может быть приведено к виду  С помощью подстановки
С помощью подстановки  , т.е. y = tx однородное дифференциальное уравнение приводится к уравнению с разделяющимися переменными относительно новой неизвестной функции t(x).
, т.е. y = tx однородное дифференциальное уравнение приводится к уравнению с разделяющимися переменными относительно новой неизвестной функции t(x).
Дифференциальным уравнением второго порядка называется уравнение вида  где х – независимая переменная, y(х) – неизвестная функция этой переменной,
где х – независимая переменная, y(х) – неизвестная функция этой переменной,  и
и  – ее первая и вторая производные.
– ее первая и вторая производные.
Общее решение уравнения второго порядка имеет вид:  где С1 и С2 – две произвольные постоянные.
где С1 и С2 – две произвольные постоянные.
Решение, полученное в неявном виде  называется общим интегралом уравнения второго порядка.
называется общим интегралом уравнения второго порядка.
Уравнение вида  где p(x), q(x) и f(x) – заданные функции, называется линейным дифференциальным уравнением второго порядка. В этом уравнении искомая функция у, и ее производные
где p(x), q(x) и f(x) – заданные функции, называется линейным дифференциальным уравнением второго порядка. В этом уравнении искомая функция у, и ее производные  и
и  входят в уравнение в первых степенях и связаны линейно.
входят в уравнение в первых степенях и связаны линейно.
Если  , то уравнение называется линейным однородным дифференциальным уравнением и имеет вид:
, то уравнение называется линейным однородным дифференциальным уравнением и имеет вид: 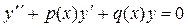 ,
,
если же 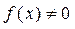 , то уравнение называется линейным неоднородным дифференциальным уравнением второго порядка.
, то уравнение называется линейным неоднородным дифференциальным уравнением второго порядка.
Общее решение линейного однородного уравнения второго порядка имеет вид:  ,где у1 и у2 – два линейно независимых частных решения этого уравнения
,где у1 и у2 – два линейно независимых частных решения этого уравнения  , а С1 и С2 – произвольные постоянные.
, а С1 и С2 – произвольные постоянные.
Общее решение линейного неоднородного уравнения имеет вид:  ,где
,где  – общее решение соответствующего однородного уравнения, а
– общее решение соответствующего однородного уравнения, а  – какое-либо частное решение неоднородного уравнения .
– какое-либо частное решение неоднородного уравнения .
Если коэффициенты при у,  и
и  – постоянные, то уравнение
– постоянные, то уравнение  где p и q – вещественные числа, называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Общее решение этого уравнения имеет вид:
где p и q – вещественные числа, называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Общее решение этого уравнения имеет вид:  ,где у1 и у2 – два линейно независимых частных решения этого уравнения, а С1 и С2 – произвольные постоянные.
,где у1 и у2 – два линейно независимых частных решения этого уравнения, а С1 и С2 – произвольные постоянные.
Для нахождения линейно независимых частных решений у1 и у2 используется квадратное уравнение вида  ,которое называется характеристическим для уравнения
,которое называется характеристическим для уравнения  .
.
Вид общего решения линейного однородного дифференциального уравнения второго порядка зависит от вида корней характеристического уравнения.
1) корни характеристического уравнения вещественные и различные  Общее решение имеет вид:.
Общее решение имеет вид:. 
2) корни характеристического уравнения вещественные и равные 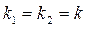 .Общее решение имеет вид:
.Общее решение имеет вид: 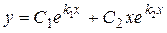
3) корни характеристического уравнения комплексно-сопряженные  Общее решение имеет вид:
Общее решение имеет вид:  ..
..
Построение общего решения неоднородного уравнения состоит из двух этапов. Сначала нужно найти общее решение соответствующего однородного уравнения  , используя характеристическое уравнение, затем найти частное решение
, используя характеристическое уравнение, затем найти частное решение  неоднородного уравнения с помощью метода вариации произвольных постоянных или метода неопределенных коэффициентов.
неоднородного уравнения с помощью метода вариации произвольных постоянных или метода неопределенных коэффициентов.
Метод вариации произвольных постоянных применяется для нахождения частного решения  линейного неоднородного дифференциального уравнения в тех случаях, когда известно общее решение
линейного неоднородного дифференциального уравнения в тех случаях, когда известно общее решение  соответствующего однородного уравнения.
соответствующего однородного уравнения.
При известном 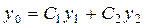 , функция
, функция  будет частным решением уравнения
будет частным решением уравнения  , если с1(х) и с2(х) удовлетворяют так называемым «условиям вариации»:
, если с1(х) и с2(х) удовлетворяют так называемым «условиям вариации»:

Метод неопределенных коэффициентов применяется для нахождения частного решения  неоднородного уравнения с постоянными коэффициентами в тех случаях, когда функция f(x), стоящая в правой части этого уравнения, имеет один из двух «специальных» видов:
неоднородного уравнения с постоянными коэффициентами в тех случаях, когда функция f(x), стоящая в правой части этого уравнения, имеет один из двух «специальных» видов:
 , где Pn(x) – многочлен степени n:
, где Pn(x) – многочлен степени n:
Pn(x) = a0 xn + a1 xn-+….+ an-1 x+ an, или  ,
,
где M и N – числа.
Пример. Найти общее решение уравнения  .
.
Решение: Найдем общее решение  линейного однородного дифференциального уравнения
линейного однородного дифференциального уравнения  . Характеристическое уравнение
. Характеристическое уравнение 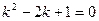 имеет вещественные равные корни
имеет вещественные равные корни  . Значит,
. Значит,  Находим частное решение исходного уравнения. В нем правая часть
Находим частное решение исходного уравнения. В нем правая часть  есть формула вида
есть формула вида  причем
причем  , не является корнем характеристического уравнения. Поэтому, частное решение
, не является корнем характеристического уравнения. Поэтому, частное решение  ищем в виде
ищем в виде  , то есть
, то есть  , где
, где 
 и
и  - неопределенные коэффициенты. Тогда
- неопределенные коэффициенты. Тогда  ,
,  Подставив
Подставив 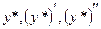 в исходное уравнение, получим
в исходное уравнение, получим  , или
, или  . Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
. Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений: 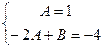
Отсюда  . Поэтому частное решение данного уравнения имеет вид
. Поэтому частное решение данного уравнения имеет вид  . Следовательно,
. Следовательно,  - искомое общее решение уравнения.
- искомое общее решение уравнения.
Пример. Решить уравнение  .
.
Решение: Находим решение однородного уравнения 
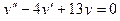
 Характеристическое уравнение
Характеристическое уравнение  имеет корни
имеет корни  . Следовательно,
. Следовательно,  . Находим частное решение
. Находим частное решение  . Правая часть линейного неоднородного дифференциального уравнения имеет вид
. Правая часть линейного неоднородного дифференциального уравнения имеет вид 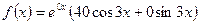 . Частное решение ищем в виде
. Частное решение ищем в виде  . Имеем:
. Имеем:  ,
, 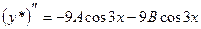 . Подставляем в исходное уравнение
. Подставляем в исходное уравнение 
или 
Получаем систему: 
Следовательно,  . Поэтому
. Поэтому  .
.
Общее решение исходного уравнения имеет вид:  .
.
Вопросы для самопроверки.
1. Какое уравнение называется дифференциальным?
2. Что такое общее решение дифференциального уравнения?
3. Сколько произвольных констант входит в общее решение дифференциального уравнения?
4. Сколько начальных условий необходимо для нахождения частного решение дифференциального равнения третьего порядка?
5. Что такое интегральная кривая?
6. Что такое линейное дифференциальное уравнение?
7. Как найти общее решение линейного дифференциального уравнения?
8. Что такое характеристическое уравнение?
Тема 9. РЯДЫ.
Понятие числового ряда. Сходимость и расходимость. Сходимость рядов с положительными членами, признак Даламбера, интегральный признак. Знакопеременные и знакочередующиеся ряды, абсолютная и условная сходимость, признак Лейбница. Понятие функционального ряда. Область сходимости. Степенные ряды, радиус сходимости. Ряд Тейлора.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Бесконечная сумма чисел u1 + u2 +…+ un +… (или  ), где каждое число ип можно вычислить, зная его номер п, называется числовым рядом.
), где каждое число ип можно вычислить, зная его номер п, называется числовым рядом.
При этом формула un = f(n), позволяющая найти каждый член ряда, называется формулой общего члена ряда.
Сумма конечного числа п первых членов ряда называется частичной суммой ряда: sn = u1 + u2 +…+ un
Если существует конечный предел частичных сумм ряда: 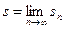 ,
,
то говорят, что ряд сходится, а число s называется суммой ряда. Если конечный  не существует, то ряд (1.1) называется расходящимся.
не существует, то ряд (1.1) называется расходящимся.
Замечание. Таким образом, свойства числовых рядов во многом определяются свойствами числовых последовательностей {sn}.
Примеры. 1) Ряд  сходится, так как представляет собой бесконечно убывающую геометрическую прогрессию со знаменателем
сходится, так как представляет собой бесконечно убывающую геометрическую прогрессию со знаменателем  , сумму которой можно найти по формуле
, сумму которой можно найти по формуле  .
.
2)Рассмотрим ряд  . Представим общий член ряда в виде:
. Представим общий член ряда в виде:  . Тогда частичная сумма sn будет выглядеть так:
. Тогда частичная сумма sn будет выглядеть так:  .Тогда
.Тогда 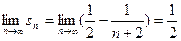 . Следовательно, ряд сходится, и его сумма равна
. Следовательно, ряд сходится, и его сумма равна  .
.
3)Ряд 1+1+1+…+1+… расходится, так как 
4) Ряд 1-1+1-1+…+(-1)п+1+… тоже расходится, так как последовательность его частичных сумм имеет вид: s1 = 1, s2 = 0, s3 = 1, s4 = 0 и т.д., а такая последовательность предела не имеет.
|
из
5.00
|
Обсуждение в статье: Тема8. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

