 |
Главная |
Функциональные ряды. Область сходимости.
|
из
5.00
|
Бесконечная сумма функций u1(x) + u2(x) +…+ un(x) +… ,
где un(x) = f (x , n), называется функциональным рядом.
Если задать конкретное числовое значение х, то указанный ряд превратится в числовой ряд, причем в зависимости от выбора значения х такой ряд может сходиться или расходиться. Практическую ценность представляют только сходящиеся ряды, поэтому важно определить те значения х, при которых функциональный ряд становится сходящимся числовым рядом.
Множество значений х, при подстановке которых в функциональный ряд получается сходящийся числовой ряд, называется областью сходимости функционального ряда.
Функция s ( x ), определенная в области сходимости ряда, которая для каждого значения х из области сходимости равна сумме соответствующего числового ряда, полученного из функционального ряда при данном значении х, называется суммой функционального ряда.
Пример. Найдем область сходимости и сумму функционального ряда
1 + х + х² +…+ xn +…
При |x| ≥ 1  поэтому соответствующие числовые ряды расходятся. Если же |x| < 1, рассматриваемый ряд представляет собой сумму бесконечно убывающей геометрической прогрессии, вычисляемую по формуле:
поэтому соответствующие числовые ряды расходятся. Если же |x| < 1, рассматриваемый ряд представляет собой сумму бесконечно убывающей геометрической прогрессии, вычисляемую по формуле:  .
.
Следовательно, областью сходимости ряда является интервал (-1, 1), а его сумма имеет указанный вид.
Замечание. Так же, как для числовых рядов, можно ввести понятия частичной суммы функционального ряда:
sn = 1 + х + х² +…+ xn и остатка ряда: rn = s – sn .
Степенным рядом называется функциональный ряд вида 
Замечание. С помощью замены х – х0 = t ряд (5.1) можно привести к виду  , поэтому все свойства степенных рядов достаточно доказать для рядов вида
, поэтому все свойства степенных рядов достаточно доказать для рядов вида 
Теорема (1-я теорема Абеля). Если степенной ряд сходится при х = х0 , то при любом x: |x | < | x 0 | ряд сходится абсолютно. Если же ряд расходится при х = х0 , то он расходится при любом x: |x | > | x 0 |.
Таким образом, если найти наибольшее из чисел х0 > 0 таких, что степенной ряд сходится при х = х0 , то областью сходимости данного ряда, как следует из теоремы Абеля, будет интервал (- х0 , х0 ), возможно, включающий одну или обе границы.
Число R ≥ 0 называется радиусом сходимости степенного ряда, если 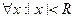 этот ряд сходится, а
этот ряд сходится, а 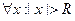 расходится. Интервал (- R , R ) называется интервалом сходимости ряда.
расходится. Интервал (- R , R ) называется интервалом сходимости ряда.
Примеры.
1) Для исследования абсолютной сходимости ряда 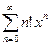 применим признак Даламбера:
применим признак Даламбера:  . Следовательно, ряд сходится только при х = 0, и радиус его сходимости равен 0: R = 0.
. Следовательно, ряд сходится только при х = 0, и радиус его сходимости равен 0: R = 0.
2) Используя тот же признак Даламбера, можно показать, что ряд  сходится при любом х , то есть
сходится при любом х , то есть 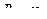
3) Для ряда  по признаку Даламбера получим:
по признаку Даламбера получим:
 Следовательно, при –1 < x < 1 ряд сходится, при x < -1 и x > 1 расходится. При х = 1 получаем гармонический ряд, который, как известно, расходится, а при х = -1 ряд
Следовательно, при –1 < x < 1 ряд сходится, при x < -1 и x > 1 расходится. При х = 1 получаем гармонический ряд, который, как известно, расходится, а при х = -1 ряд  сходится условно по признаку Лейбница. Таким образом, радиус сходимости рассматриваемого ряда R = 1, а интервал сходимости – [-1, 1).
сходится условно по признаку Лейбница. Таким образом, радиус сходимости рассматриваемого ряда R = 1, а интервал сходимости – [-1, 1).
Формулы для определения радиуса сходимости степенного ряда:
1. Формула Даламбера.
Рассмотрим степенной ряд  и применим к нему признак Даламбера: для сходимости ряда необходимо, чтобы
и применим к нему признак Даламбера: для сходимости ряда необходимо, чтобы  .Если существует
.Если существует  , то область сходимости определяется неравенством
, то область сходимости определяется неравенством  , то есть
, то есть  -формула Даламбера для вычисления радиуса сходимости.
-формула Даламбера для вычисления радиуса сходимости.
2. Формула Коши-Адамара.
Используя радикальный признак Коши и рассуждая аналогичным образом, получим, что можно задать область сходимости степенного ряда как множество решений неравенства  при условии существования этого предела, и, соответственно, найти еще одну формулу для радиуса сходимости:
при условии существования этого предела, и, соответственно, найти еще одну формулу для радиуса сходимости:  - формула Коши-Адамара.
- формула Коши-Адамара.
Представление функции в виде 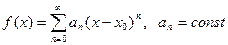 называется ее разложением в степенной ряд. Пусть функция f ( x ) определена в некоторой окрестности точки х0 и имеет в этой точке производные всех порядков. Тогда ряд
называется ее разложением в степенной ряд. Пусть функция f ( x ) определена в некоторой окрестности точки х0 и имеет в этой точке производные всех порядков. Тогда ряд 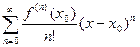 называется рядом Тейлора.
называется рядом Тейлора.
Пример. Найдем разложение в ряд Тейлора при х0 = 0 функции f ( x ) = 2x .
 . Следовательно,
. Следовательно,  .
.
Если при разложении в ряд Тейлора принимается х0 = 0, то полученный ряд  называется рядом Маклорена.
называется рядом Маклорена.
|
из
5.00
|
Обсуждение в статье: Функциональные ряды. Область сходимости. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

