Определенный интеграл и его свойства. Геометрический смысл интеграла. Формула Ньютона-Лейбница. Замена переменной в определенном интеграле.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.

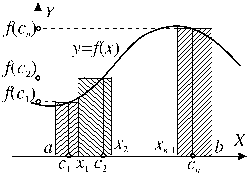
Пусть на промежутке [a;b] задана функция f(x). Будем считать функцию непрерывной. Выберем на промежутке [a;b] произвольные числа x₁, x₂, x₃, ¼, x_n-1, удовлетворяющие условию: a< x₁,< x₂<¼< x_n-1,<b. Эти числа разбивают промежуток [a;b] на n более мелких промежутков: [a;x₁], [x₁;x₂], ¼ [x_n-1;b]. На каждом из этих промежутков выберем произвольно по одной точке: c₁Î[a;x₁], c₂Î[x₁;x₂], ¼ c_nÎ[x_n-1;b].

Введем обозначения:Dx₁ = x₁ – a; Dx₂ = x₂ – x₁; ¼ Dx_n = b – x_n-1.

Составим сумму: .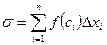

Она называется интегральной суммой функции f(x) по промежутку [a;b]. Очевидно, что интегральная сумма зависит от способа разбиения промежутка и от выбора точек c_i.

Каждое слагаемое интеграль­ной суммы представляет собой площадь прямоугольника, покрытого штриховкой на рисунке.

Введем обозначение: l = max(Dx_i), i = 1, 2, ¼ n.. Величину l иногда называют параметром разбиения.

Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что величина l стремится к нулю. Определенным интегралом 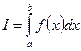 от функции  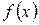по промежутку [a;b] называется предел, к которому стремится интегральная сумма при этом процессе, если предел существует: .

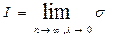Если такой предел существует, то он не зависит от первоначального разбиения промежутка [a;b] и выбора точек c_i.

Число a называется нижним пределом интегрирования, а число b ¾ верхним пределом интегриро­вания.

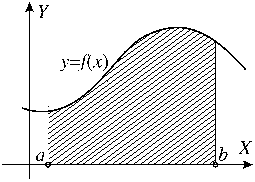
Рассмотрим фигуру, ограниченную графиком непрерывной, неотрицательной на промежутке [a;b] функции f(x), отрезком [a;b] оси X, и прямыми x = a; x = b. Такую фигуру называют криволинейной трапецией. На рисунке криволинейная трапеция выделена штриховкой. Площадь S этой трапеции определяется формулой .

Перечислим свойства определенного интеграла:

1) 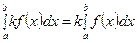  (здесь k ‑ произвольное число);

2) ;

3) ;

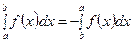4) Если c Î[a;b], то .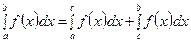

Из этих свойств следует, например, что .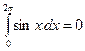

Все приведенные выше свойства непосредственно следуют из определения определенного интеграла.

Пусть функция f(t) определена и непрерывна на некотором промежутке, содержащем точку a . Тогда каждому числу x из этого промежутка можно поставить в соответствие число 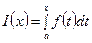, определив тем самым на промежутке функцию I(x), которая называется определенным интегралом с переменным верхним пределом. Отметим, что в точке x = a эта функция равна нулю. Вычислим производную этой функции в точке x. Для этого сначала рассмотрим приращение функции в точке x при приращении аргумента Dx: DI(x) = I(x + Dx) – I(x) =

.

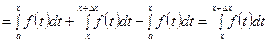Производная определенного интеграла по верхнему пределу в точке x равна значению подынтегральной функции в точке x. Отсюда следует, что функция 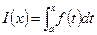 является первообразной для функции f(x), причем такой первообразной, которая принимает в точке x = a значение, равное нулю. Этот факт дает возможность представить определенный интеграл в виде 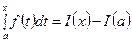. (1)

Пусть F(x) тоже является первообразной для функции f(x), тогда по теореме об общем виде всех первообразных функции I(x) = F(x) + C, где C — некоторое число. При этом правая часть формулы (1) принимает вид

I(x) – I(a) = F(x) + C – (F(a) +C) = F(x) – F(a).                                          (2)

Из формул (1) и (2) после замены x на b следует формула для вычисления определенного интеграла от функции f(t) по промежутку [a;b]:

                                      ,

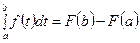которая называется формулой Ньютона-Лейбница. Здесь F(x) — любая первообразная функции f(x).

Для того, чтобы вычислить определенный интеграл от функции f(x) по промежутку [a;b], нужно найти какую-либо первообразную F(x) функции f(x) и подсчитать разность значений первообразной в точках b и a. Разность этих значений первообразной принято обозначать символом .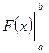

Приведем примеры вычисления определенных интегралов с помощью формулы Ньютона-Лейбница.

Примеры.

1. .

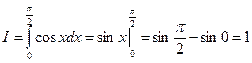2. .

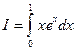Сначала вычислим неопределенный интеграл от функции f(x) = xe^x. Используя метод интегрирования по частям, получаем: 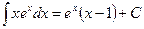. В качестве первообразной функции f(x) выберем функцию e^x(x – 1) и применим формулу Ньютона-Лейбница:

I = e^x(x 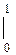– 1) = 1.

При вычислении определенных интегралов можно применять формулу замены переменной в определенном интеграле: .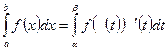

Здесь a и b определяются, соответственно, из уравнений j(a) = a; j(b) = b, а функции f, j, j ¢ должны быть непрерывны на соответствующих промежутках.

Пример: .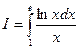

Сделаем замену: ln x = t или x = e^t, тогда если x = 1, то t = 0, а если x = e, то t = 1. В результате получим: .

При замене переменной в определенном интеграле не нужно возвращаться к исходной переменной интегрирования.

Из геометрического смысла определенного интеграла для областей имеет место формула для вычисления площади, в которой 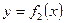- уравнение верхней границы области, а 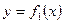-уравнение нижней границы области:  .

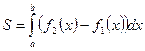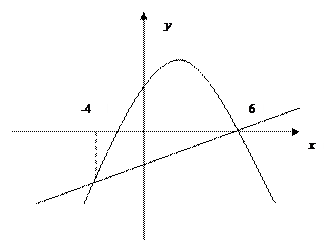
Пример. Вычислить площадь фигуры, ограниченной параболой 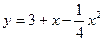 и прямой .

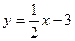Решение. Найдем точки пересечения параболы и прямой: .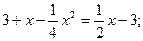

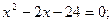
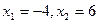Получаем: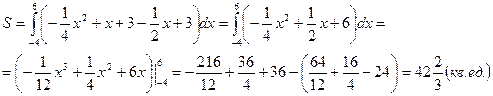

Вопросы для самопроверки.

1. Что такое интегральная сумма? Каков ее геометрический смысл?

2. В чем геометрический смысл определенного интеграла?

3. Каковы основные свойства определенного интеграла?

4. Что такое формула Ньютона-Лейбница? Как ее применяют при вычислении определенного интеграла?

5. В чем особенность замены переменной в определенном интеграле?