Простейшие свойства сходящихся рядов.

· Исключение или добавление конечного числа слагаемых не влияет на сходимость ряда.

· Если сходится ряд u₁ + u₂ +…+ u_n +… и его сумма равна s , то сходится и ряд cu₁ + cu₂ +…+ cu_n +…, сумма которого равна cs .

· Если ряды  а₁ + а₂ +…+ а_п +… и b₁ + b₂ +…+ b_n +…сходятся и их суммы соответственно равны s_a и s_b, то ряды (a₁ + b₁) + (a₂ + b₂) +… и (a₁ – b₁) + (a₂ – b₂) +… тоже сходятся, и их суммы равны s_a + s_b  и s_a – s_b .

Необходимое условие сходимости ряда.

Главным вопросом при исследовании числового ряда является вопрос о его сходимости или расходимости. Сформулируем необходимое условие сходимости ряда, то есть условие, при невыполнении которого ряд расходится.

Теорема Если ряд (1.1) сходится, то

Замечание. Это условие является необходимым, но не достаточным признаком сходимости, то есть из стремления общего члена ряда к нулю не обязательно следует сходимость ряда.

Для ряда  ряд называется n - м остатком данного ряда.

Обозначим сумму остатка ряда (при условии, что он сходится) через . Если ряд сходится, то сходится и любой его остаток, и наоборот – из сходимости какого-либо остатка ряда следует сходимость ряда в целом.

Теорема. Если ряд (1.1) сходится, то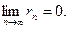

Пусть для всех членов ряда (1.1) выполнено условие u_n ≥ 0.

Теорема (критерий сходимости). Ряд с неотрицательными членами сходится тогда и только тогда, когда его частичные суммы ограничены сверху.

При исследовании числовых рядов на сходимость непосредственный поиск предела частичных сумм является в большинстве случаев весьма затруднительным. Вместо этого удобно использовать специальные признаки сходимости рядов.

Интегральный признак Коши.

Теорема  Если функция f неотрицательна и убывает на полупрямой х ≥ 1, то ряд  сходится или расходится одновременно с несобственным интегралом .

Пример. Применим интегральный признак Коши к исследованию сходимости рядов вида , сравнивая их с интегралами  Рассмотрим следующие возможные значения α:

а) α > 1. Тогда  (так как при α > 1 ). Следовательно, несобственный интеграл сходится, а значит, сходится и рассматриваемый ряд.

б) α = 1. При этом  - интеграл расходится, поэтому расходится и ряд.

в) α < 1. Тогда  (так как при α < 1 ). Из расходимости несобственного интеграла следует расходимость исследуемого ряда.

Замечание. Итак, ряд вида  сходится при α > 1 и расходится при

α ≤ 1. Это свойство ряда  будет часто использоваться в дальнейшем.

Признаки сравнения.

Теорема (1-й признак сравнения). Если для двух рядов с положительными членами u₁ + u₂ +…+ u_n +… (1) и v₁ + v₂ +…+ v_n +… (2) выполнено условие u_n ≤ v_n, то:

а) если ряд (2) сходится, то сходится и ряд (1);

б) если ряд (1) расходится, то расходится и ряд (2).

Следствие. Условие u_n ≤ v_n  может выполняться начиная не обязательно с п = 1. Утверждение теоремы справедливо, если это условие выполняется для всех п, больших некоторого N .

Пример. Исследуем на сходимость ряд , сравнив его с рядом . Этот ряд сходится, так как последовательность его членов представляет собой бесконечно убывающую геометрическую прогрессию со знаменателем 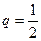, сумма которой равна . При любом n > 1 n∙ 2ⁿ > 2ⁿ , следовательно, , поэтому исследуемый ряд сходится.

Теорема (2-й признак сравнения). Если для рядов (1) и (2) выполнено условие  то ряды (1) и (2) сходятся и расходятся одновременно.

Следствие. При применении 2-го признака сравнения удобно брать в качестве ряда, с которым сравнивается данный ряд, ряд вида . Напомним еще раз, что такой ряд сходится при α > 1 и расходится при 

α ≤ 1.

Пример. Общий член ряда  можно представить в виде  (разделив числитель и знаменатель на х). Теперь очевидно, что . Поскольку ряд  сходится (так как α = 2 >1), сходится и исходный ряд.

Признак Даламбера.

Теорема.  Если для ряда , u_n > 0, существует предел 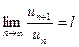, то при l < 1 ряд сходится, а при l > 1 расходится.

Замечание. При l = 1 признак Даламбера не дает ответа на вопрос о сходимости ряда (ряд в этом случае может и сходиться, и расходиться).

Пример. Применим признак Даламбера к исследованию сходимости ряда .

 , следовательно, ряд сходится

(учитываем, что (п + 1)! = п!(п + 1) ).