 |
Главная |
Комплексные числа. Операции с комплексными числами. Представление в прямоугольной системе координат.
|
из
5.00
|
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Комплексным числом z называют выражение вида 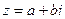 (алгебраическая форма записи), где
(алгебраическая форма записи), где  и
и  - действительные числа, i- мнимая единица.
- действительные числа, i- мнимая единица.
Замечание.Алгебраическая запись комплексных чисел позволяет производить операции над ними по обычным правилам алгебры.
Комплексное число  называется комплексно сопряженным числу
называется комплексно сопряженным числу 
Арифметические операции над комплексными числами проводятся по правилам действий над многочленами  и
и  , считая
, считая  .
.
Пример. Даны комплексные числа  ,
, 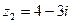 . Найти их сумму, произведение и частное.
. Найти их сумму, произведение и частное.
Решение.  .
.



Комплексное число z = (a,b) можно представить в виде точки на плоскости с координатами (a,b) или вектора с началом в начале координат и концом в точке (a,b).Запись вида z = ρ (cos φ + isin φ) называется тригонометрической формой записи комплексного числа.
В свою очередь, модуль и аргумент комплексного числа можно выразить через а и b:  . Следовательно, аргумент комплексного числа определен не однозначно, а с точностью до слагаемого, кратного 2π.
. Следовательно, аргумент комплексного числа определен не однозначно, а с точностью до слагаемого, кратного 2π.
Частным случаем операции умножения является возведение в степень:  - формула Муавра.
- формула Муавра.
Используя полученные соотношения, перечислим основные свойства комплексно сопряженных чисел:
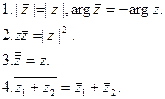
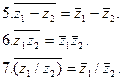
Комплексное число  называется корнем n -й степени из z , если z = z1n .
называется корнем n -й степени из z , если z = z1n .
Пример. Число z = 16 можно представить в тригонометрической форме следующим образом: z = 16(cos0 + isin0). Найдем все значения  :
:
Введем еще одну форму записи комплексного числа. На множестве комплексных чисел существует связь между тригонометрическими и показательными функциями, задаваемая формулой Эйлера:  , Используя эту формулу, можно получить еще один вид комплексного числа:
, Используя эту формулу, можно получить еще один вид комплексного числа:  , который называется показательной формой записи комплексного числа.
, который называется показательной формой записи комплексного числа.
Вопросы для самопроверки
1.Что такое мнимая единица?
1. Что такое вещественная и мнимая части комплексного числа? Являются ли они вещественными числами?
2. Что такое комплексно сопряженные числа? Чем отличаются изображения комплексно сопряженных чисел z и z* на комплексной плоскости?
3. Как изобразить на комплексной плоскости, пользуясь правилами сложения векторов, сумму и разность двух комплексных чисел7
4. Чему равно произведение комплексно сопряженных чисел?
ТЕМА 4. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИЙ.
Понятие предела. Предел суммы, произведения и частного. Предел сложной функции. Вычисление пределов. Замечательные пределы. Понятие непрерывности в точке и на интервале. Точки разрыва. Геометрический смысл. Непрерывность суммы, произведения и частного функций. Непрерывность сложной функции. Непрерывность элементарных функций.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Число A называется пределом функции y = f(x) в точке x0 (иногда говорят, при x, стремящемся к x0), если для любого положительного числа e можно найти такое положительное число d, что для всех x из d-окрестности точки x0 соответствующие значения y попадают в e-окрестность точки y = A.
Можно сформулировать определение предела функции по-другому. Число A называется пределом функции y = f(x) в точке x0, если для любого положительного числа e можно найти такое положительное число d, что для всех x, удовлетворяющих условию
0 < êx – x0ê < d, выполняется неравенство êy – Aê < e.
Тот факт, что A есть предел функции y = f(x) в точке x = x0, записывается формулой  .
.
Функция y = f(x) называется непрерывной в точке x = x0, если она определена в этой точке и ее значение f(x0) равно пределу функции в этой точке:  .
.
Примеры. Функция y = x2 непрерывна в точке x = 2, как и во всех точках числовой оси.
Функция  не является непрерывной в точке x = 2.
не является непрерывной в точке x = 2.
Функция  не является непрерывной в точке x = 0.
не является непрерывной в точке x = 0.
 Функция, непрерывная в каждой точке открытого промежутка, называется непрерывной на этом промежутке.
Функция, непрерывная в каждой точке открытого промежутка, называется непрерывной на этом промежутке.
Свойства предела функции.
1. Функция не может иметь в одной точке два разных предела.
2.  , если C — постоянная функция.
, если C — постоянная функция.
3. Если существует  и C — постоянная функция, то
и C — постоянная функция, то  .
.
4. Если существуют  и
и  , то существует
, то существует 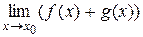 , равный
, равный  , а также существует
, а также существует  , равный
, равный  . Если при этом
. Если при этом 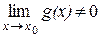 , то существует
, то существует  , равный
, равный  .
.
Число B называется пределом функции f(x) в точке a справа (это записывается в виде формулы  ), если для любого положительного числа e найдется положительное число d, такое что из условия 0 < x – a < d будет следовать êB –f(x) ê < e.
), если для любого положительного числа e найдется положительное число d, такое что из условия 0 < x – a < d будет следовать êB –f(x) ê < e.
Согласно приведенному определению  .
.
Число С называется пределом функции f(x) в точке b слева (это записывается в виде формулы  ), если для любого положительного числа e найдется положительное число d такое, что из условия 0 < b – x < d будет следовать êC – f(x)ê < e.
), если для любого положительного числа e найдется положительное число d такое, что из условия 0 < b – x < d будет следовать êC – f(x)ê < e.
Функция f(x) называется непрерывной в точке a справа (непрерывной в точке b слева), если
 (
(  ).
).
Функция  непрерывна справа в точке x=0.
непрерывна справа в точке x=0.
Функция называется непрерывной на замкнутом промежутке [a, b], если она непрерывна на открытом промежутке (a, b), непрерывна справа в точке a и непрерывна слева в точке b.
Для того, чтобы выполнялось равенство  , необходимо и достаточно, чтобы одновременно выполнялись два равенства:
, необходимо и достаточно, чтобы одновременно выполнялись два равенства:
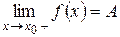 ;
; 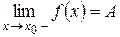
Два, так называемых, "замечательных предела".
1.  . Геометрический смысл этой формулы заключается в том, что прямая
. Геометрический смысл этой формулы заключается в том, что прямая  является касательной к графику функции
является касательной к графику функции  в точке
в точке  .
.
2.  . Здесь e — иррациональное число, приблизительно равное 2,72.
. Здесь e — иррациональное число, приблизительно равное 2,72.
Примеры. Найти пределы функций: а)  ,
,
б) 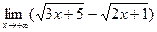 , в)
, в) 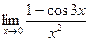 .
.
Решение .
а) Непосредственной подстановкой  в числитель и знаменатель убеждаемся, что имеем неопределенность вида
в числитель и знаменатель убеждаемся, что имеем неопределенность вида 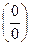 . Обращение числителя и знаменателя в ноль показывает, что многочлены (в числителе и знаменателе) имеют общий корень
. Обращение числителя и знаменателя в ноль показывает, что многочлены (в числителе и знаменателе) имеют общий корень  . Разложив многочлены на множители и сократив на общий множитель
. Разложив многочлены на множители и сократив на общий множитель 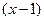 , получим:
, получим:
 .
.
б) Имеем неопределенность типа  , умножим и разделим на сопряженное выражение:
, умножим и разделим на сопряженное выражение:

в) Используя формулу понижения степени  и первый «замечательный» предел, получим:
и первый «замечательный» предел, получим:
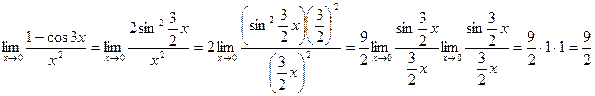
Вопросы для самопроверки.
1.Приведите пример функции, не имеющей предела в данной точке.
2.При каких условиях из существования пределов слева и справа следует существование предела функции в данной точке.
3.Какова связь между понятиями предела функции и бесконечно малой функции?
4.Какова связь между бесконечно малой и бесконечно большой функцией?
5.Чему равен предел суммы четырех функций?
6.В чем различие между понятиями предела и непрерывности функции в точке?
|
из
5.00
|
Обсуждение в статье: Комплексные числа. Операции с комплексными числами. Представление в прямоугольной системе координат. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

