ТЕМА 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ.

Понятие производной. Геометрический смысл. Правила вычисления производных. Производная сложной функции. Таблица производных. Производные высших порядков. Возрастание и убывание функций. Экстремумы, выпуклость, вогнутость, точки перегиба. Асимптоты. Построение графиков.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Рассмотрим функцию y=f(x), непрерывную в некоторой окрестности точки x. Пусть Dx приращение аргумента в точке x. Обозначим через D y или Df приращение функции, равное f(x+Dx) – f(x).

Отношение Df /Dx, как видно из рисунка 1, равно тангенсу угла a, который составляет секущая MN кривой y = f(x) c положительным направлением горизонтальной оси координат.

Отношение Dy / Dx или, что то же самое (f(x + Dx)  f(x)) / Dx , можно рассматривать при заданном x как функцию аргумента Dx . Эта функция не определена в точке Dx = 0. Однако её предел в этой точке может существовать. Если существует предел отношения (f(x + Dx) – f(x)) / Dx в точке Dx = 0, то он называется производной функции y = f(x)в точке x и обозначается y ¢ или f ¢(x): .

Нахождение производной функции y = f(x)называется дифференцированием.

Если для любого числа x из открытого промежутка (a, b) можно вычислить f ¢(x), то функция f(x) называется дифференцируемой на промежутке (a, b).

Геометрический смысл производной заключается в том, что произ­водная функции f(x)в точке x равна тангенсу угла наклона касательной к графику функции в этой точке.

Уравнение касательной в точке с координатами имеет вид: .

Уравнение нормали (прямой, проходящей через точку касания перпендикулярно касательной) имеет вид:

Пример. Написать уравнение касательной и нормали к кривой в точке М₀(0;1).

Решение. Найдем первую производную ; . Искомые уравнения касательной:   или ; нормали:  или .

Производная - это скорость изменения функции в точке x. Из определения производной следует, что , причем точность этого приближенного равенства тем выше, чем меньше Dx. Производная f ¢ (x) является приближенным коэффициентом пропорциональности между Df  и Dx.

Таблица производных элементарных функций.

f(x)			f(x)			f(x)
C	0		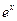			cosx	-sinx
x	1		lnx	1/x		tgx	1/cos2x
xn	nxn-1		ax	axlna		arcsina
	1/(2 )					arccosa	-
1/x	-1 / x2		sinx	cosx		arctgx	1/(1+x2)

Основные свойства производной.

1. Если функция имеет производную в точке, то она непрерывна в этой точке.

2. Если существует f ¢ (x) , и С ‑ произвольное число, то функция  имеет производную: (Cf(x))¢ = Cf ¢ (x).

3. Если существуют f ¢ (x)и g ¢ (x), то функция S(x) = f(x) + g(x) имеет производную: S ¢ (x) = f ¢ (x) + g ¢ (x).

4. Если существуют f ¢ (x) и g ¢ (x), то функция P(x) = f(x)g(x) имеет производную: P ¢ (x) = f ¢ (x)g(x) + f(x)g ¢ (x).

5. Если существуют f ¢ (x) и g ¢ (x) и при этом g(x) ¹ 0, то функция 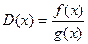имеет производную: .

Производная сложной функции.

Пусть функция g(x) имеет производную в точке x, а функция f(z) имеет производную в точке z = g(x). Тогда сложная функция F(x) = f(g(x))имеет в точке x производную F ¢ (x) = f ¢ (z) g¢ (x).

Примеры. Найтипроизводные функций: а) , б) , в) .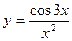

Решение. а) Данная функция представляет собой сумму двух функций, поэтому воспользуемся свойством 3. Получим: .

б) Данная функция является произведением двух функций, ее производную найдем с помощью свойства 4.

в) Данная функция является частным двух функций. Применим свойство 5.

.

     Пусть функция y = f ( x ) дифференцируема на некотором отрезке [a ; b]. В таком случае ее производная представляет собой тоже некоторую функцию х. Продифференцировав эту функцию, мы получим так называемую вторую производную (или производную второго порядка) функции f ( x ). Продолжая эту операцию, можно получить производные третьего, четвертого и более высоких порядков. При этом f `( x ) будем называть производной первого порядка.

Производной n -го порядка (или n -й производной) от функции f ( x ) называется производная (первого порядка) от ее ( n -1)-й производной.

Обозначение: у^{( n )} =( y ^{( n -1)})΄= f ^{( n )} ( x ). Производные 2-го и 3-го порядка обозначаются соответственно y ′ ΄ и y΄ ′ ΄ .

Свойства производных высших порядков.

Основные свойства производных высших порядков следуют из соответствующих свойств первой производной:

1. (cf(x))⁽ⁿ⁾=c·f⁽ⁿ⁾(x).

2. (f(x)+g(x))⁽ⁿ⁾=f⁽ⁿ⁾(x)+g⁽ⁿ⁾(x).

3. Для y=x^m y⁽ⁿ⁾=n(n-1)…(n-m+1)x^m-n. Если m – натуральное число, то при n > m y ^{( n )} =0.