Радиус-вектор, перемещение и скорость

       При движении материальной  точки ее радиус-вектор изменяется во времени: r = r(t).

Определение 2.1 Траекторией материальной точки называется кривая, вычерчиваемая в пространстве концом ее радиус- вектора

Определение 2.2 Перемещением материальной точки называется изменение ее радиус-вектора за рассматриваемый интервал времени:                                  (2.1)

Определяемый соотношением (2.1) вектор перемещения Δr принципиально отличается от пройденного пути Δs, являющемся скалярной величиной, равной длине отрезка криволинейной траектории, заключенного между концами вектора перемещения (рис. 2.1).

Рис. 2.1. Траектория материальной точки,
ее перемещение и пройденный путь за время Δt

Широко используемой характеристикой движения является его скорость. Важно помнить, что скорость является величиной векторной и различать среднюю и мгновенную скорости движения.

Определение  2.3 Средней скоростью материальной точки называется отношение перемещения к интервалу времени, за которое оно произошло:

                                            (2.2)

Представленное в векторной форме определение (2.2) может быть записано как совокупность трех аналогичных ему скалярных равенств:

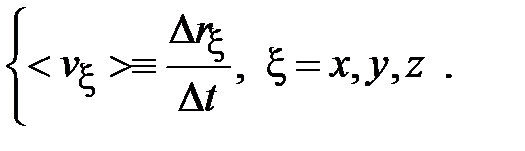
Определение 2.4 Мгновенной скоростью материальной точки называется ее средняя скорость за очень короткий промежуток времени:

                                     (2.3)

В математике и физике столь часто встречается операция вычисления отношения приращения функции к приращению ее аргумента при условии стремления к нулю последнего, что для описанной операции было введено специальное название дифференцирование. Функция, возникающая в результате дифференцирования исходной называется ее производной. Т.о. мгновенная скорость материальной точки является производной от ее радиус-вектора. В соотношении (2.3) и далее для обозначения бесконечно-малых приращений вместо символа «Δ» используется символ «d».

Из определений 2.1 – 2.4 и соотношений (2.1 – 2.3) следуют общие свойства скорости:

· вектор средней скорости направлен по вектору перемещения, т.е. по секущей, а вектор мгновенной скорости – по касательной к траектории материальной точки;

· каждая из трех компонент вектора средней скорости численно равна тангенсу угла наклона секущей, а вектора мгновенной скорости – по касательной к графику зависимости от времени соответствующей компоненты радиус-вектора.

                                          .                                  (2.4)

На рис. 2.2 представлены примеры использования графического и численного (пакет символьных вычислений Wolframe Mathematica) дифференцирования для нахождения компоненты скорости материальной точки по известной зависимости ее координаты от времени.

Рис. 2.2.Примеры вычисления производной функции: методом графического дифференцирования и с помощью пакета символьных вычислений
Wolfram Mathematica

Задача определения координат материальной точки по известным зависимостям от времени проекций решается с помощью операции интегрирования, являющейся обратной по отношению к дифференцированию. Из определения мгновенной скорости (2.3) следует, что каждая компонента вектора элементарного перемещения материальной точки за бесконечно малый интервал времени может быть найдена как площадь бесконечно-узкой полоски под графиком зависимости от времени соответствующей компоненты вектора скорости (рис. 2.3):

.

Перемещение Δr за конечный интервал времени длительностью Δt (от часто выбираемого равным нулю момента t₀ до t = t₀ + Δt) получается в результате суммирования элементарных перемещений и для каждой из компонент вектора dr . Каждая из трех компонент вектора полного перемещения Δr_ξ оказывается равной площади под графиком зависимости от времени соответствующей компоненты вектора мгновенной скорости.

Рис. 2.3.Примеры вычисления определенного и неопределенного интегралов от  функции: графическим методом и с помощью пакета символьных вычислений Wolfram Mathematica

Соответствующая нахождению площади под графиком скалярной  функции математическая операция носит название вычисления определенного интеграла в пределах от t₀ (нижний предел) до t (верхний предел):

                                                                         (2.5)

Ключевым этапом вычисления определенного интеграла (2.5) является нахождение определяемой с точностью до константы первообразной функции, производная от которой совпадает с подынтегральным выражением. Это обратное дифференцированию действие, называемое взятием неопределенного интеграла, не имеет однозначного алгоритма и по существу сводится к угадыванию первообразной. Вычисление определенного интеграла завершается нахождением константы интегрирования, которая выбирается так, чтобы при совпадении пределов интегрирования (t = t₀) его величина оказывалась равной нулю.

Вычисление по (2.5) приращения каждой из трех координат материальной точки за рассматриваемый временной интервал движения в соответствии с (2.1) позволяет вычислить радиус-вектор движущейся материальной точки, если известно его начальное значение ( r(t= t₀) = r₀ ):

                               (2.6)

Соотношения (2.3) и (2.6) позволяют рассчитывать скорости по известным зависимостям радиус-векторов от времени и радиус-векторы их начальным значениям и заданным зависимостям скоростей от времени.

Пример 2.1. Скорость при равноускоренном движении Рассчитать мгновенную  скорость материальной точки, радиус-вектор которой квадратично зависит от времени:

Решение. Будет показано, что приведенная в условии зависимость r(t) соответствует равноускоренному движению, что пока не существенно. Согласно определению (2.3) вектор мгновенной скорости материальной точки вычисляется как производная ее радиус-вектора по времени:

Приведенный вывод хорошо известной формулы для скорости при равноускоренном движении иллюстрирует идеи доказательства двух полезных теорем математического анализа: «производная суммы нескольких функций равна сумме их производных» и «производная от произведения функции на постоянный множитель (в том числе- векторный) равна произведению производной от функции на этот множитель».

Скорость и ускорение

При движении материальной точки вектор ее мгновенной скорости, как и радиус-вектор, в общем случае изменяется во времени v = v(t). По аналогии с координатным пространством можно ввести пространство скоростей, где вдоль координатных осей отложены компоненты вектора скорости (рис. 2.4). Аналогом траектории в таком пространстве является годограф вектора скорости. Продолжая аналогию, целесообразно ввести среднюю и мгновенную скорости изменения скорости, соответственно называемые векторами среднего и мгновенного ускорений.

Рис. 2.4. Радиус-вектор и траектория материальной точки в координатном пространстве и их аналоги в пространстве скоростей: вектор скорости и его годограф.

	Определение 2.5 Средним ускорением материальной точки называется отношение приращения ее скорости к интервалу времени, за которое оно произошло.
	Определение 2.6 Мгновенным ускорением материальной точки называется ее среднее ускорение за очень короткий промежуток времени

Из определений 2.3 – 2.6 непосредственно следует, что мгновенное ускорение связано с мгновенной скоростью абсолютно аналогично тому, как мгновенная скорость связана с радиус-вектором. Правильность математических соотношений не нарушается при замене одних переменных, входящих в эти соотношения, на другие. Математическая эквивалентность (с точностью до переобозначений {r, v} → {v, a}) приводит к тому, что любому верному соотношению, связывающему радиус-вектор материальной точки и ее скорость, соответствует верный аналог, связывающий векторы скорости и ускорения:

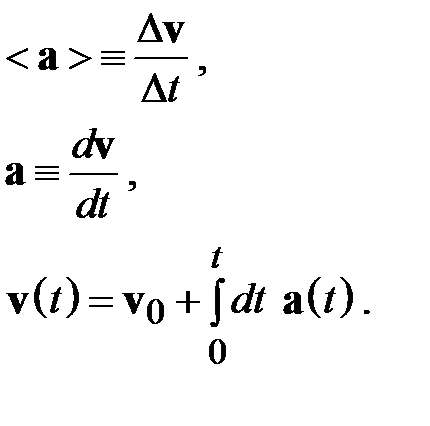                                     (2.7)

Для записи связи между  мгновенным ускорением с радиус-вектором удобно использовать введенную в математике операцию вычисления второй производной:

                                                                 (2.8)

Пример 2.2. Равномерное вращение по окружности Рассчитать мгновенную скорость материальной точки, проекции радиус-вектора которой изменяются во времени по закону:

Решение. Легко убедиться в том, что приведенным в условии зависимостям проекций радиус-вектора от времени соответствует движение по окружности:

                                                              (2.9)

Для вычисления компонент вектора скорости необходимо продифференцировать по времени оба равенства системы (2.9). Соответствующие выкладки иллюстрируют чисто математические идеи вывода правил дифференцирования сложной функции и вычисления производных от синуса и косинуса:

В приведенных выше вычислениях учтены два достаточно очевидных для физика, но аккуратно доказываемых в математике факта: значения синусов малых углов примерно равны самим углам, измеряемым в радианной мере; косинусы малых углов могут считаться равными 1. Далее будет считаться, что читатель не имеет проблем с дифференцированием тригонометрических и сложных функций.

Дифференцирование системы уравнений (2.9) легко приводит к выражениям для компонент вектора скорости, из которых следует известное из элементарных курсов выражение для величины линейной скорости при равномерном вращении по окружности.

             (2.10)

 При рассматриваемом движении годограф вектора скорости, как и траектория, представляет собой окружность (рис. 2.5). Из отмечавшейся аналогии (2.7) между парами векторов {r , v } и {v , a } следует, что величина ускорения (скорости изменения скорости) получается домножением радиуса годографа на угловую частоту вращения: |а| = ω·(ωR). Этот же результат получается более строго путем дифференцирования (2.10) по времени. В результате оказывается, что вектор ускорения материальной точки противонаправлен ее радиус-вектору, проведенному из центра окружности. По этой причине получившееся ускорение называют центростремительным:

                   (2.11)

Рис. 2.5. Траектория и годограф скорости при равномерном вращении
материальной точки по окружности