 |
Главная |
Связи между линейными и угловыми скоростями и ускорениями
|
из
5.00
|
При повороте на бесконечно-малый угол приращение радиус-вектора оказывается равным векторному произведению угла поворота на его исходное значение (рис. 3.3), что с учетом (3.17) позволяет получить связь линейной и угловой скорости частицы, движущейся по окружности:
 (3.21)
(3.21)
Выражение для линейного ускорения при движении по окружности получается при подстановки в (2.7) выражения для линейной скорости (3.21):
 . (3.22)
. (3.22)
В случае движения с постоянной угловой скоростью дифференцирование в (3.22) не представляет сложности и с учетом правила (3.16) приводит к известному из элементарного курса и полученному в Примере 2.2 выражению (2.11) для центростремительного ускорения. В общем случае движения с переменной угловой скоростью в (3.22) требуется вычислить производную от произведения двух зависящих от времени векторных функций. Подобные задачи столь часто встречаются и в математике, и в физике, что целесообразно продемонстрировать идею вывода правила дифференцирования произведения на данном конкретном примере.
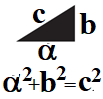
| Теорема 3.4. О дифференцировании произведения двух функций
Производная от произведения двух функций вычисляется как сумма произведений производной первой функции на вторую и первой функции на производную второй:
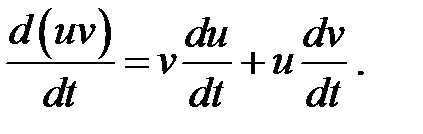 (3.23) (3.23)
|
Доказательство правила (3.23), справедливого для произведений как скалярных, так и векторных функций, будет продемонстрировано на примере векторного произведения.
Правило дифференцирования произведения легко выводится из определения производной:




 .
.
В случае дифференцирования произведений скалярных функций и скалярного произведения векторных функций от скалярного аргумента выведенное правило сохраняет свою справедливость. Это объясняется тем, что использованные при выводе свойства дистрибутивности для операций сложения и умножения как скалярных, так и векторных величин идентичны и, следовательно, следствия этих свойств совпадают. Что же касается такой особенности операции векторного перемножения двух векторов, как анти коммутативность, то она не оказывается существенной, поскольку в приведенном выводе никаких перестановок местами сомножителей не осуществлялось.
Подстановка (3.18) в результат дифференцирования (3.22) по правилу (3.23) приводит к окончательному выражению для линейного ускорения тела, движущегося по окружности:
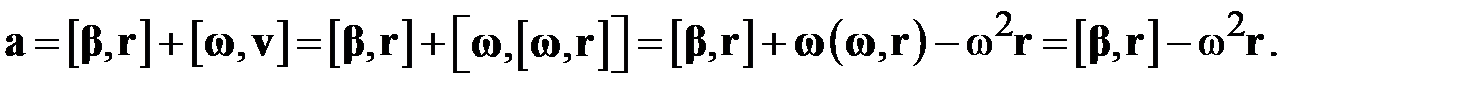 (3.24)
(3.24)
Первое из слагаемых в (3.24) представляет собой компоненту ускорения, направленную по касательной к траектории и «несущую ответственность» за изменение величины (модуля) скорости тела. Такую составляющую ускорения называют тангенциальной. Второе слагаемое представляет собой нормальное или центростремительное ускорение, направленное к центру окружности и «несущее ответственность» за искривление траектории.
В случае произвольного криволинейного движения (рис. 3.4) небольшие участки траектории можно аппроксимировать дугами окружностей, на которых ускорение может быть разложено на нормальную и тангенциальную составляющие:
 (3.25)
(3.25)

|
Рис. 3.4. Разложение ускорения на нормальное и тангенциальное в общем случае (слева) и его использование для аппроксимации участка траектории дугой окружности
Знание величин нормального ускорения из (3.25) и линейной скорости (3,21) весьма полезно при аппроксимации участков криволинейной траектории дугами окружностей и вычисления их радиусов кривизны:
 (3,26)
(3,26)

| Пример 3.2. Вычисление радиуса кривизны траектории Найти радиус кривизны траектории тела, брошенного под углом к горизонту, в точке максимального подъема тела. |
Решение. Нормальное и тангенциальное ускорения тела, брошенного под углом к горизонту брошенного под углом к горизонту тела вектор его ускорения (ускорения свободного падения) направлен вертикально вниз. В точке максимальной высоты подъема вектор мгновенной скорости направлен горизонтально и имеет величину v = v0 cosα, где v0 - величина начальной скорости, α – угол бросания тела. Из сказанного следует, что в верхней точке траектории нормальное или центростремительное ускорение совпадает с ускорением свободного падения. Из (3.26) следует:
 .
.
Т.о. параболическую траекторию брошенного под углом к горизонту тела в верхней точке можно аппроксимировать окружностью найденного радиуса.

| Вопросы и задачи для самостоятельной работы |
1. Первоначально покоившаяся материальная точка начинает двигаться по окружности радиусом R с постоянным угловым ускорением β. Получить явные зависимости от времени декартовых координат и проекций линейной скорости и ускорения (rx(t), vx(t), ax(t), x = x, y). Найти величину линейного ускорения тела через время Т после начала его движения.
2. Найти радиус кривизны траектории тела, брошенного под углом к горизонту в каждой точке его траектории.
3. Карусели, вращающиеся с угловой скоростью ω, начинают равномерно тормозиться и останавливаются, сделав N оборотов. Сколько времени длилось торможение?
4. Эллипс имеет полуоси a и b. Чему равен максимальный и минимальный радиусы кривизны кривой, ограничивающей эллипс. Указание – воспользоваться решениями задач на расчет скорости и ускорения материальной точки, вращающейся по эллипсу с постоянной угловой скоростью.
5. Покоившееся тело начинает двигаться по окружности радиусом R с постоянным угловым ускорением β. Какова будет величина (модуль) линейного ускорения тела через время Т после начала движения?
6. Колесо радиусом R равномерно катится без проскальзывания по горизонтальной поверхности так, что ось колеса движется с постоянной скоростью V. Куда направлены и чему равны мгновенные скорости следующих трех точек обода колеса: самой нижней; самой верхней; расположенной на одной высоте с осью колеса?
7. Стержень длиной L может вращаться в вертикальной плоскости вокруг одного из своих концов, укрепленного на шарнире на высоте L над горизонтальной поверхностью Земли. В исходном состоянии стержень покоится, почти касаясь своим свободным концом поверхности. К этому концу прикрепляется груз и стержень начинает вращаться так, что его угловое ускорение возрастает со временем по линейному закону: β(t) = γ·t. В тот момент, когда, сделав N полных оборотов, стержень принял горизонтальное положение, груз отделился от стержня и полетел вертикально вверх. На какую максимальную высоту поднимется груз?
Лекция 4
|
из
5.00
|
Обсуждение в статье: Связи между линейными и угловыми скоростями и ускорениями |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

