 |
Главная |
Равноускоренное движение
|
из
5.00
|

| Определение 2.7 Равноускоренным называется движение, при котором вектор мгновенного ускорения не зависит от времени |
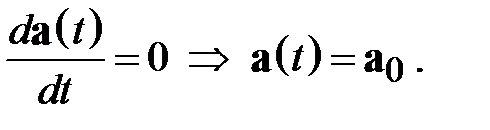 (2.12)
(2.12)
Вычисляя по (2.7) скорость по известному ускорению, легко показать (например, путем вычисления площадей под графиками) что при равноускоренном движении скорость является линейной функцией времени:
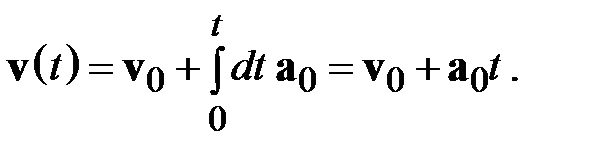 (2.13)
(2.13)
Из (2.7) и (2.13) так же показывается, что при равноускоренном движении координата является квадратичной функцией времени:
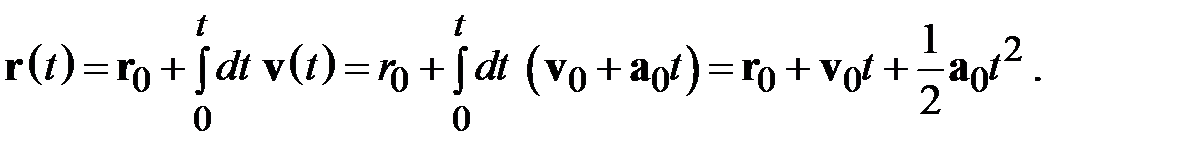 (2.14)
(2.14)
Соотношения (2.13) и (2.14) дают исчерпывающее описание равноускоренного движения.
Частным случаем равноускоренного движения является движение с нулевым ускорением, при котором радиус-вектор частицы оказывается линейной функцией времени. Такое движение называется равномерным прямолинейным. Его частным является состояние покоя. Важным для современной релятивистской физики свойством состояний равномерного прямолинейного движения и покоя является их физическая неразличимость для наблюдателя, находящегося в замкнутой системе отсчета. Весьма далеко идущие следствия из такой неразличимости будут рассмотрены в последующих разделах .
Другой частный случай прямолинейного равноускоренного движения реализуется при сонаправленных начальной скорости и ускорения. В этом случае удобно так выбрать систему отсчета К, чтобы одна из осей (например, х) была ориентирована вдоль векторов a0 и v0. Это обеспечивает возможность сведения векторного описания равноускоренного движения к скалярному:
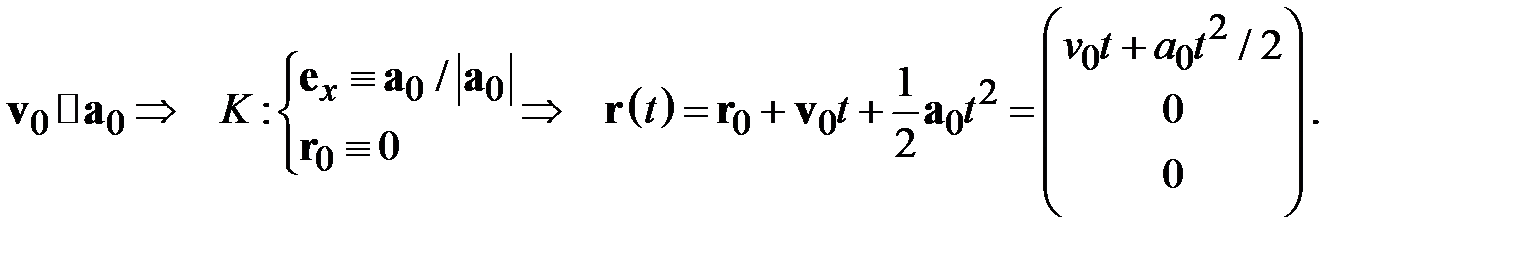
Для одномерного равноускоренного движения может быть сформулирован ряд утверждений о его свойствах, учет которых иногда существенно облегчает решение задач:
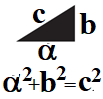
| Теорема 2.1.
При равноускоренном движении средняя скорость равна полусумме начальной и конечной скоростей точечного тела.
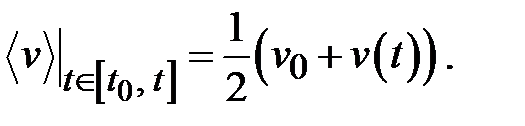
|
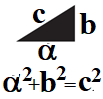
| Теорема 2.2 Изменение координаты точечного тела при равноускоренном движении равно разности квадратов его конечной и начальной скоростей, отнесенной к удвоенному ускорению:
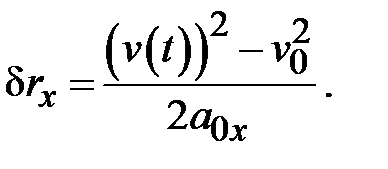
|
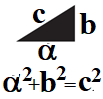
| Теорема 2.3
Равноускоренно движущееся первоначально покоившееся тело за равные промежутки времени проходит отрезки путей, относящиеся между собой как последовательные нечетные числа:
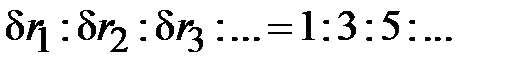 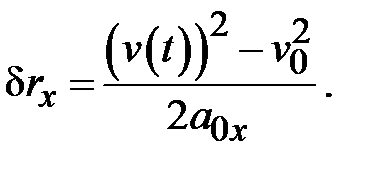
|
Доказательства сформулированных теорем приводятся во многих элементарных курсах физики и в рамках настоящего изложения должны быть получены учащимися самостоятельно.
Практически важным примером приложения формул для равноускоренного движения является анализ движения тела, брошенного под углом к горизонту, на котором базируется такая до сих пор популярная дисциплина, как баллистика.

| Пример 2.3. Движение тела, брошенного под углом к горизонту Рассмотреть особенности движения тел вблизи поверхностей планет, при котором взаимодействия с другими объектами пренебрежимо мало, а ускорение свободного падения может считаться постоянным |
Решение задачи в удобной для анализа системе отсчета с удачным выбором начала координат и направления декартовых осей (рис. 2.6) позволяет существенно упростить математические выкладки:
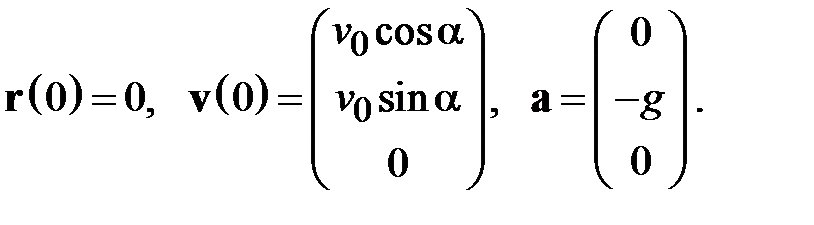 (2.15)
(2.15)
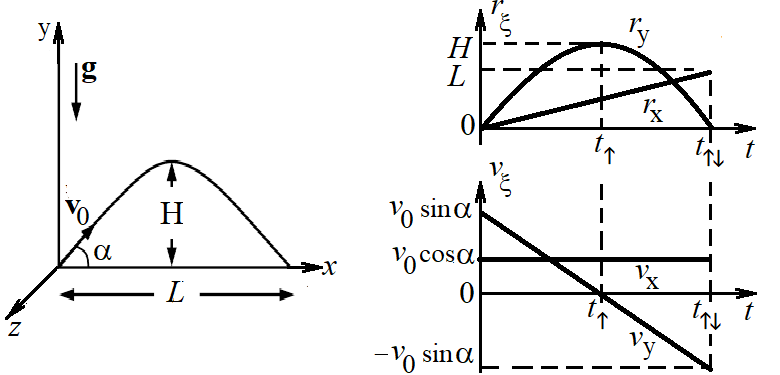
Рис. 2.6. Движение тела, брошенного под углом к горизонту: система координат, траектория и зависимости от времени координат и проекций скорости материальной точки
Зависимость от времени компонент скорости тела, брошенного под углом к горизонту, и его координат дается общими формулами равноускоренного движения (2.13) и (2.14) с учетом конкретизации (2.15):
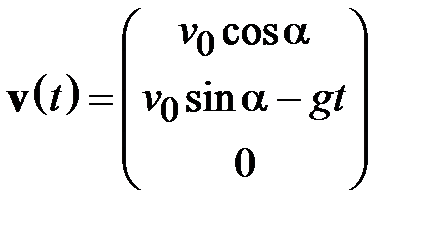 , (2.16)
, (2.16)
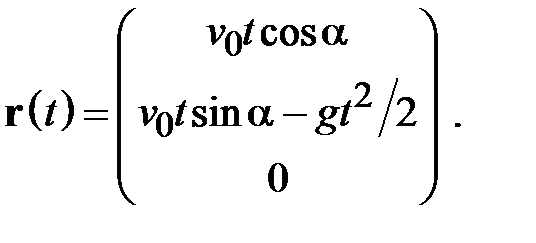 (2.17)
(2.17)
Время подъема Т↑ определяемое из условия обращения в ноль вертикальной компоненты скорости в верхней точке траектории, позволяет найти максимальную высоту подъема Н:
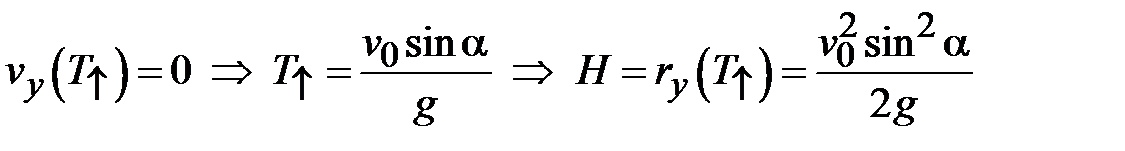 . (2.18)
. (2.18)
Для расчета дальности полета определяется интервал времени Т↑↓ до момента, когда тело окажется на исходной высоте ry = 0. Это время оказывается в два раза большим, чем время подъема Т↑. Последнее означает, что в случает отсутствия сопротивления воздуха времена подъема и спуска брошенного тела совпадают друг с другом. В результате дальность полета оказывается пропорциональной квадрату начальной скорости и синусу удвоенного угла бросания:
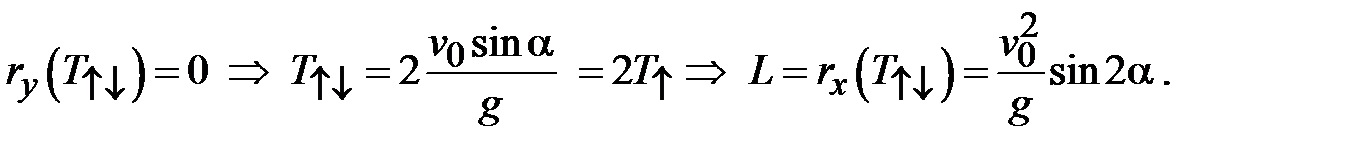 (2.19)
(2.19)
Уравнение траектории тела, брошенного под углом к горизонту, получается в результате исключения времени из двух уравнений для координат (2.17):
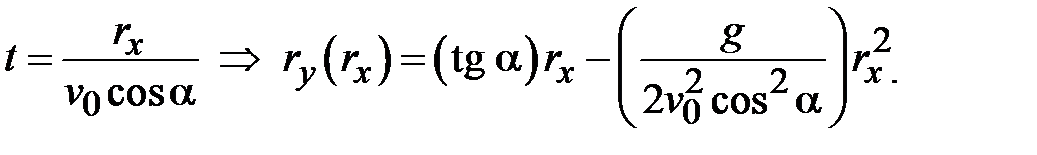 (2.20)
(2.20)

| Пример 2.4. Движение тела с постоянной скоростью изменения ускорения Рассмотреть особенности одномерного прямолинейного движения первоначально покоившегося в начале координат тела, ускорение которого начинает возрастать во времени по линейному закону от нулевого значения в начальный момент времени. |
Решение. В описанной в условии ситуации временная зависимость скорости изменения ускорения («тряски») полностью аналогична зависимости от времени скорости изменения скорости (ускорения):
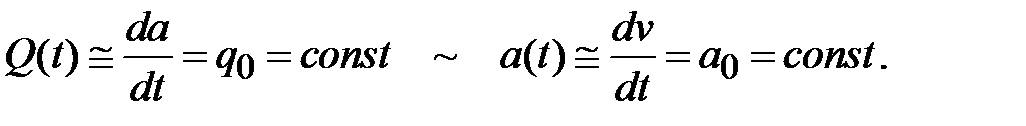 .
.
Из аналогии между определениями скоростей изменения ускорения и скорости следует, что в рассматриваемом случае временное поведение ускорения полностью аналогично поведению скорости при равноускоренном движении:
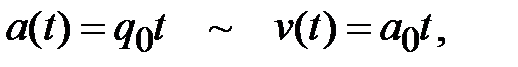
а зависимость v(t) оказывается подобной зависимости от времени координаты при прямолинейном равноускоренном движении первоначально покоившегося тела:
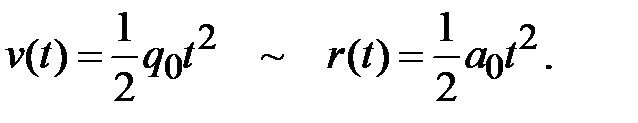
На следующем шаге вычисления перемещения тела при движение с увеличивающимся ускорением построенная цепочка аналогий с (2.12) – (2.14), позволяющая находить кинематические характеристики движения с Q ( t) = const графически обрывается. Для нахождения перемещения при рассматриваемом движении следовало бы вычислять площадь под параболой. В соответствии с (2.5) центральным этапом в решении задачи является нахождение первообразной от квадратичной функции. Используя уже возникший в практике расчетов производных опыт, нетрудно убедиться в том, что соответствующее перемещение, имеет вид кубической параболы, производная от которой дает найденное выражение для скорости:
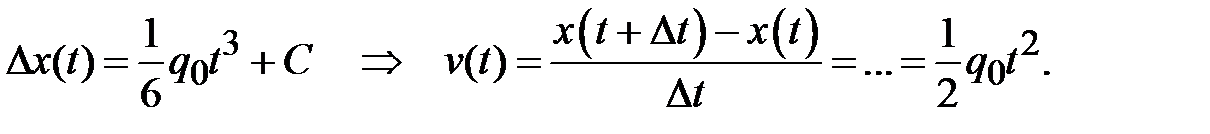
Математическая запись проделанной операции «угадывания» первообразной (записывается в квадратных скобках) и последующей подстановки подстановки пределов интегрирования имеет следующий вид:
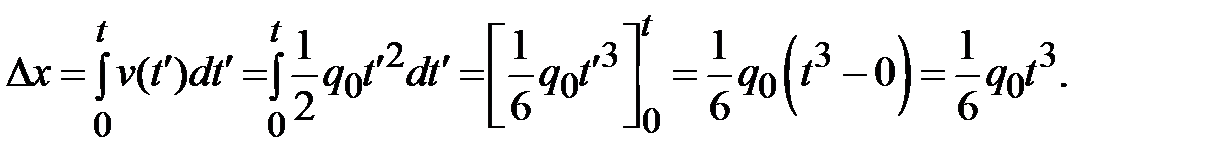
|
из
5.00
|
Обсуждение в статье: Равноускоренное движение |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

