 |
Главная |
Векторное произведение
|
из
5.00
|
Векторное произведение двух векторов может быть введено в трехмерном пространстве, как антикоммутативная операция, ставящая в соответствие двум сомножителям псевдовектор:
 .
.

| Определение 3.3 Векторным произведением двух векторов в трехмерном пространстве называется вектор, направленный перпендикулярно плоскости, задаваемой перемножаемыми векторами, в направлении, определяемом правилом «правой руки», длина которого численно равна площади параллелограмма, построенного на перемножаемых векторах (рис. 3.2): |
 (3.11)
(3.11)

|
Рис. 3.2. Правило выбора направления векторного произведения двух векторов и геометрический смысли смешанного скалярно-векторного произведения
Из определения следует, что векторное произведение двух параллельно направленных векторов (в том числе и векторное произведение вектора на себя) равно нулю.
В курсе математики доказывается ряд полезных теорем о векторном произведении, которые будут постоянно использоваться в курсе физики:
| Теорема 3.1
Скалярное произведение векторного произведения дух векторов на третий вектор («смешанное скалярно-векторное произведение») численно равно объему параллелепипеда, построенного на перемножаемых векторах (рис. 3.2) и не изменяется при циклической перестановке сомножителей:
 (3.12) (3.12)
|
| Теорема 3.2
Векторное произведение линейно по своим сомножителям:
 (3.13) (3.13)
|
| Теорема 3.3: Декартовы компоненты векторного произведения двух векторов вычисляются через координаты сомножителей согласно:
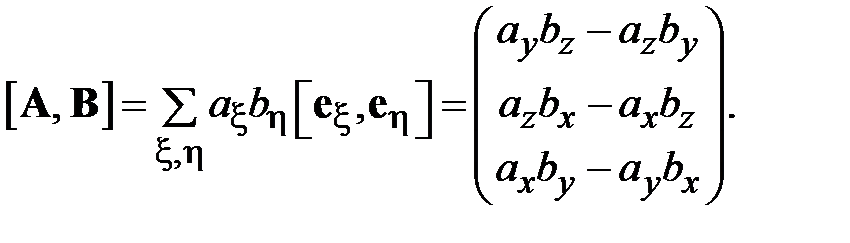 (3.14) (3.14)
|
Использование широко распространенного в математике понятия определителя позволяет переписать выражение (3.14) в эквивалентном виде, который окажется весьма удобным в дальнейшем:
 . (3.15)
. (3.15)
Помимо смешанных скалярно-векторных произведений в физике весьма часто возникают двойные векторные произведения (векторное произведение вектора на векторное произведение двух векторов). Применение к таким объектам соотношений (3.14) и (3.15) привело бы к весьма громоздким математическим выражениям. Во многих случаях вычисления существенно упрощаются в результате использования правила «БАЦ минус ЦАБ»:
| Теорема 3.4:
Двойное векторное произведение является вектором, вычисляемым согласно:
 (3.16) (3.16)
|
Соотношения (3.12) – (3.16) обосновываются в курсе алгебры, но могут быть доказаны читателем самостоятельно сразу после того, как будет продемонстрировано удобство из использования для описания криволинейного движения материальной точки.
|
из
5.00
|
Обсуждение в статье: Векторное произведение |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

