 |
Главная |
И 63. Свободные и вынужденные колебания
|
из
5.00
|
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются при- мерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).
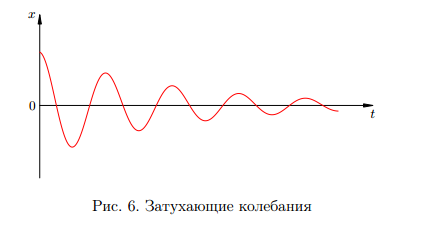
Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы F(t), периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна ω0, а вынуждающая сила
зависит от времени по гармоническому закону:
F(t) = Fо Cos ωt .
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой ω вынуждающей силы (внешняя сила как бы навязывает системе свою частоту). Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.
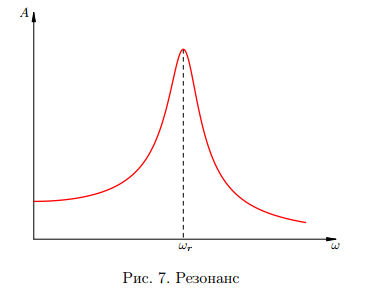
Мы видим, что вблизи частоты ω = ωr наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: ωr ≈ ω0, и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, ωr = ω0, а амплитуда колебаний возрастает до бесконечности при ω → ω0.
Автоколебания
Наблюдая колебания листьев деревьев, дорожных знаков над проезжей частью улиц, полотнищ на ветру и др., мы понимаем, что во всех перечисленных случаях незатухающие колебания происходят за счет энергии постоянно дующего ветра. При этом сама колебательная система производит отбор энергии ветра в нужный момент времени и в количестве, требуемом для компенсации неизбежно присутствующих энергетических потерь. Колебания в этих системах начинаются самопроизвольно за счет начальных флуктуаций (дрожаний) колеблющихся предметов. Частота и амплитуда установившихся колебаний определяется как параметрами самой системы, так и параметрами ее взаимодействия с ветром. Такие колебания являются примерами автоколебаний, а сами системы – примерами автоколебательных систем. Классическим примером автоколебательной системы служат механические часы с маятником и гирями. Эти часы периодически «черпают» энергию при опускании гирь, подвешенных к цепочке, перекинутой через шестерню часового механизма.
Принцип работы всех автоколебательных систем можно понять, обратившись к схеме, изображенной на рис. 3.5 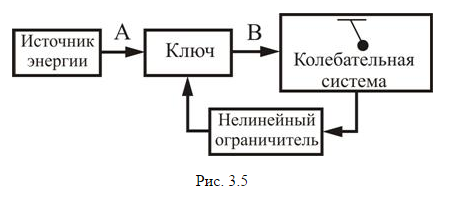
Периодическим поступлением энергии в колебательную систему от источника энергии по каналу АВ управляет сама колебательная система посредством обратной связи. Схематически это изображено в виде некоторого запирающего канал АВ устройства (ключа), который управляется самой системой. Так, в зависимости от положения и скорости колеблющегося листа на ветру будет различной мощность сил аэродинамического давления.
В конструкции часового механизма (рис. 3.6) присутствует специальное устройство – анкер, выполняющий роль ключа. Этот анкер, представляющий собой коромысло, приводится в колебание самим маятником часов. При определенных положениях он «отпирает» одну из шестерен часового механизма. В этот момент времени шестерня проворачивается за счет момента сил, приложенного со стороны натянутой цепи с грузом. Груз при этом опускается на небольшую величину. Количество энергии, поступающей в часовой механизм, равно по величине уменьшению потенциальной энергии груза в поле силы тяжести.
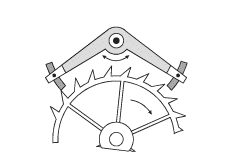
Рис. 3.6
Важно отметить, что любая автоколебательная система нелинейна. На схеме это отражено наличием в системе обратной связи нелинейного ограничителя сигнала, управляющего ключом. Нелинейность системы проявляется в том, что при начальном нарастании амплитуды колебаний, порожденных флуктуациями, поступление энергии в систему за каждый последующий период колебаний увеличивается нелинейно, т.е. прирост поступающей энергии становится все меньше и меньше. Естественно, что амплитуда колебаний достигнет такой установившейся величины, при которой приток энергии и ее потери будут равны.
65.Малые колебания.
Очень распространенный тип движения механических систем представляют собой так называемые малые колебания, которые система совершает вблизи своего положения устойчивого равновесия. Рассмотрение этих движений мы начнем с наиболее простого случая, когда система имеет всего одну степень свободы.
Устойчивому равновесию соответствует такое положение системы, в котором ее потенциальная энергия U(q) имеет минимум; отклонение от такого положения приводит к возникновению силы —dU/dq, стремящейся вернуть систему обратно. Обозначим соответствующее значение обобщенной координаты через q0. При малых отклонениях от положения равновесия в разложении разности U(q)−U(q0) по степеням q−q0достаточно сохранить первый неисчезающий член. В общем случае таковым является член второго порядка
U (q) − U (q0) ≈ 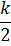 (q − q0)2,
(q − q0)2,
где k — положительный коэффициент (значение второй производной U”(q) при q=q0). Будем в дальнейшем отсчитывать потенциальную энергию от ее минимального значения (т.е. положим U(q0)=0) и введем обозначение
x = q − q0 (21.1)
для отклонения координаты от ее равновесного значения. Таким образом,
U (x) = 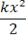 . (21.2)
. (21.2)
Кинетическая энергия системы с одной степенью свободы имеет в общем случае вид
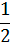 α (q)
α (q) 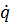 2 =
2 = 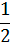 α (q)
α (q) 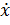 2.
2.
В том же приближении достаточно заменить функцию α(q) просто ее значением при q=q0. Вводя для краткости обозначение
α (q0) = m,
получим окончательно следующее выражение для лагранжевой функции системы, совершающей одномерные малые колебания:
L = 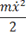 −
− 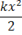 . (21.3)
. (21.3)
Соответствующее этой функции уравнение движения гласит:
m 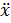 + kх = 0, (21.4)
+ kх = 0, (21.4)
или
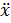 + ω2х = 0, (21.5)
+ ω2х = 0, (21.5)
где введено обозначение
ω = 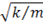 . (21.6)
. (21.6)
Два независимых решения линейного дифференциального уравнения (21.5): cos ωt и sin ωt, так что его общее решение
x = c1 cos ωt + c2 sin ωt. (21.7)
Это выражение может быть написано также и в виде
x = α cos (ωt + 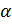 ). (21.8)
). (21.8)
Поскольку cos(ωt+ 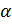 )=cosωt×cos
)=cosωt×cos 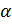 −sinωt×sin
−sinωt×sin 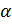 , сравнение с (21.7) показывает, что произвольные постоянные α и
, сравнение с (21.7) показывает, что произвольные постоянные α и 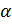 связаны с постоянными c1и c2 соотношениями
связаны с постоянными c1и c2 соотношениями
α = 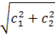 , tg
, tg 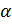 = −c2⁄c1. (21.9)
= −c2⁄c1. (21.9)
Таким образом, вблизи положения устойчивого равновесия система совершает гармоническое колебательное движение. Коэффициент а при периодическом множителе в (21.8) называется амплитудой колебаний, а аргумент косинуса — их фазой; 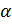 есть начальное значение фазы, зависящее, очевидно, от выбора начала отсчета времени. Величина ω называется циклической частотой колебаний; в теоретической физике, впрочем, ее называют обычно просто частотой, что мы и будем делать в дальнейшем.
есть начальное значение фазы, зависящее, очевидно, от выбора начала отсчета времени. Величина ω называется циклической частотой колебаний; в теоретической физике, впрочем, ее называют обычно просто частотой, что мы и будем делать в дальнейшем.
Частота является основной характеристикой колебаний, не зависящей от начальных условий движения. Согласно формуле (21.6) она всецело определяется свойствами механической системы как таковой. Подчеркнем, однако, что это свойство частоты связано с предполагаемой малостью колебаний и исчезает при переходе к более высоким приближениям. С математической точки зрения оно связано с квадратичной зависимостью потенциальной энергии от координаты.
Энергия системы, совершающей малые колебания, есть
E = 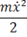 +
+ 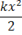 =
=  (
( 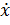 2 + ω2x2)
2 + ω2x2)
или, подставив сюда (21.8):
E = 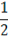 mω2α2. (21.10)
mω2α2. (21.10)
Она пропорциональна квадрату амплитуды колебаний.
Зависимость координаты колеблющейся системы от времени часто оказывается удобным представлять в виде вещественной части комплексного выражения
x = Reе{Aeiωt}, (21.11)
где А — комплексная постоянная; написав ее в виде
A = αei 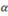 , (21.12)
, (21.12)
мы вернемся к выражению (21.8). Постоянную A называют комплексной амплитудой; ее модуль совпадает с обычной амплитудой, а аргумент — с начальной фазой.
Оперирование с экспоненциальными множителями в математическом отношении проще, чем с тригонометрическими, так как дифференцирование не меняет их вида. При этом, пока мы производим лишь линейные операции (сложение, умножение на постоянные коэффициенты, дифференцирование, интегрирование), можно вообще опускать знак взятия вещественной части, переходя к последней лишь в окончательном результате вычислений.
Пружинный маятник
Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жесткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
Период колебаний пружинного маятника может быть вычислен по следующей формуле:
{\displaystyle T=2\pi {\sqrt {\frac {m}{k}}}}T=2Пsqrt(m/k)
где, Т-период колебаний, m-масса маятника, k-коэффициент жесткости и П-метрическая постоянная (3,14)
|
из
5.00
|
Обсуждение в статье: И 63. Свободные и вынужденные колебания |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

