 |
Главная |
Дискретные случайные величины
|
из
5.00
|
Случайная величина , обозначаемая  , называется дискретной, если она принимает
, называется дискретной, если она принимает
конечное либо счетное множество значений, т.е. множество 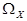 -конечное, либо счетное.
-конечное, либо счетное.
Законом распределения дискретной случайной величины называется совокупность пар
чисел  , где
, где  - возможные значения случайной величины, а
- возможные значения случайной величины, а  - вероятности, с
- вероятности, с
которыми она принимает эти значения, причем 
Зная закон распределения случайной величины, можно вычислить функцию распределения:

где суммирование распространяется на все значения индекса  , для которых
, для которых 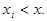
Математическим ожиданием  дискретной случайной величины
дискретной случайной величины  называется сумма произведений всех ее возможных значений и соответствующих им вероятностей:
называется сумма произведений всех ее возможных значений и соответствующих им вероятностей:

Модой дискретной случайной величины, обозначаемой  называется ее наиболее вероятное значение.
называется ее наиболее вероятное значение.
Медианой случайной величины  называется такое ее значение
называется такое ее значение  , для которого одинаково вероятно, окажется ли случайная величина меньше или больше
, для которого одинаково вероятно, окажется ли случайная величина меньше или больше  , т.е.
, т.е.

Дисперсией случайной величины называется математическое ожиданиеквадрата ее отклонения:
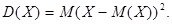
Дисперсия дискретной случайной величины вычисляется по формуле:
 или
или 
Средним квадратическим отклонением (стандартом) случайной величины  называется арифметический корень из дисперсии, т.е.
называется арифметический корень из дисперсии, т.е. 
Начальным моментом порядка  случайной величины
случайной величины  называется математическое ожидание
называется математическое ожидание  -й степени этой случайной величины, т.е.
-й степени этой случайной величины, т.е. 
Для дискретной случайной величины 
Центральным моментом порядка  случайной величины
случайной величины  называется математическое ожидание
называется математическое ожидание  -й степени отклонения
-й степени отклонения 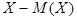 , т.е.
, т.е. 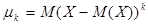 .
.
Для дискретной случайной величины 
Биноминальным называют закон распределения дискретной случайной величины  - числа появлений событий в
- числа появлений событий в  независимых испытаниях, в каждом из которых вероятность появления события равна
независимых испытаниях, в каждом из которых вероятность появления события равна 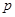 ; вероятность возможного значения
; вероятность возможного значения  ( числа
( числа  появлений события ) вычисляют по формуле Бернулли :
появлений события ) вычисляют по формуле Бернулли :  , где
, где  . При этом матема-тическое ожидание и дисперсия соответственно равны:
. При этом матема-тическое ожидание и дисперсия соответственно равны: 
Наивероятнейшее число  появлений событий в
появлений событий в  независимых испытаниях определяется по формуле:
независимых испытаниях определяется по формуле: 
Если число испытаний велико, а вероятность появления события  в каждом испытании мала, то вероятность того, что некоторое событие появиться
в каждом испытании мала, то вероятность того, что некоторое событие появиться 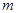 раз в
раз в 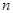 испытаниях, приближенно вычисляется по формуле:
испытаниях, приближенно вычисляется по формуле:
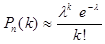 ,
,
где  - число появлений событий в
- число появлений событий в  независимых испытаниях,
независимых испытаниях,  - среднее число появлений событий в
- среднее число появлений событий в  испытаниях. Случайная величина, характеризующая число наступлений события
испытаниях. Случайная величина, характеризующая число наступлений события 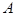 в
в  независимых испытаниях, распределена по закону Пуассона , если
независимых испытаниях, распределена по закону Пуассона , если 
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона:

Геометрическое распределение возникает в том случае, когда производится серия испытаний до первого появившегося события 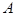 . Тогда распределение случайной величины
. Тогда распределение случайной величины  имеет вид:
имеет вид:

| 1 | 2 | 3 | … | 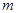 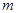
| … |

| 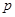
| 
| 
| … | 
| … |
Вероятность появления события 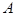 в каждом испытании постоянна и равна
в каждом испытании постоянна и равна  , т.е.
, т.е.
 и
и 
Математическое ожидание и дисперсия случайной величины, распределенной по геометрическому закону, соответственно равны:

Гипергеометрический закон распределения используется при проверке качества продукции. Проверяется  изделий, и известно, что среди этих изделий имеется
изделий, и известно, что среди этих изделий имеется 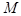 изделий, которые обладают некоторым признаком
изделий, которые обладают некоторым признаком  , а остальные
, а остальные  - признаком
- признаком 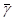 . Для проверки производится выборка, содержащая
. Для проверки производится выборка, содержащая  изделий. Определить вероятность того, что среди этих изделий
изделий. Определить вероятность того, что среди этих изделий 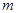 изделий обладают некоторым признаком
изделий обладают некоторым признаком  . Для определения вероятности используется классический способ задания вероятности. Число элементарных событий будет определяться числом сочетаний
. Для определения вероятности используется классический способ задания вероятности. Число элементарных событий будет определяться числом сочетаний
 и
и  ,
,
где 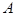 - событие, состоящее в том, что в выборке
- событие, состоящее в том, что в выборке 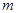 объектов обладают признаком
объектов обладают признаком  .
.
Закон распределения дискретной случайной величины  , характеризующей число появлений события
, характеризующей число появлений события  раз в
раз в  испытаниях имеет вид:
испытаниях имеет вид:
· Если 

| 0 | 1 | 2 | … | 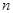
|

| 
| 
| 
| 
|
· Если 

| 0 | 1 | ….. | 
|

| 
| 
| 
|
Функция гипергеометрического распределения имеет вид

Гипергеометрический закон стремится к биноминальному закону распределению, если  при
при  и его числовые характеристики следующие
и его числовые характеристики следующие
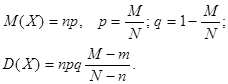
3.2. Непрерывные случайны величины.
Случайная величина  называется непрерывной, если существует такая неотрицательная,
называется непрерывной, если существует такая неотрицательная,
интегрируемая по Риману функция 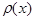 , называемая плотностью распределения вероятностей,
, называемая плотностью распределения вероятностей,
что при всех  Множество значений непрерывной
Множество значений непрерывной
случайной величины 
 - некоторый числовой интервал.
- некоторый числовой интервал.
Плотностью распределения вероятностей 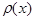 непрерывной случайной величиныХ
непрерывной случайной величиныХ
называют предел, если он существует, отношения вероятности попадания случайной величины
Х на отрезок  , примыкающей к точке
, примыкающей к точке  , к длине этого отрезка, когда
, к длине этого отрезка, когда
последний стремится к 0, т.е.
 .
.
Свойства плотности распределения вероятностей:

 - непрерывная или кусочно непрерывна функция;
- непрерывная или кусочно непрерывна функция;
Функция распределения случайной величины  – это функция
– это функция  действительной
действительной
переменной  , определяющая вероятность того, что случайная величина принимает значение
, определяющая вероятность того, что случайная величина принимает значение
меньше некоторого фиксированного числа  , т.е.
, т.е. 

Математическое ожидание и дисперсия случайной величины :
 ;
;  ;
; 
Модой непрерывной случайной величины  называется действительное число
называется действительное число  ,
,
определяемое точка максимума плотности распределения вероятностей 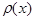 .
.
Медианой непрерывной случайной величины  называется действительное число
называется действительное число  ,
,
Удовлетворяющее условию  , т.е. корень уравнения
, т.е. корень уравнения

Начальный момент  го порядка:
го порядка:

Центральный момент  го порядка:
го порядка:

Коэффициент асимметрии или «скошенности» распределения

Коэффициент эксцесса или островершинности распределения

Случайная величина 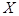 называется центрированной, если
называется центрированной, если  Если же для
Если же для
случайной величины 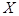
 то она называется центрированной и
то она называется центрированной и
нормированной (стандартизованной) случайной величиной.
3.3. Законы распределения непрерывной случайной величины
Равномерное распределение: Пусть плотность вероятности равна нулю всюду, кроме отрезка  , на котором все значения случайной величины Х одинаково возможны. Выражение плотности распределения вероятностей
, на котором все значения случайной величины Х одинаково возможны. Выражение плотности распределения вероятностей 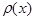 имеет следующий вид:
имеет следующий вид:

Функция равномерного распределения задается формулой:

Математическое ожидание, дисперсия и среднее квадратическое отклонение соответственно равны:
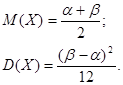

Показательное распределение. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины 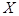 , которое описывается функцией плотности вероятности:
, которое описывается функцией плотности вероятности:

где  постоянная и называется параметром экспоненциального распределения.
постоянная и называется параметром экспоненциального распределения.
Функция распределения случайной величины, распределенной по показательному закону, имеет вид:

Математическое ожидание  . Дисперсия
. Дисперсия  , среднее квадратическое отклонение
, среднее квадратическое отклонение  .
.
Лекция №6. Нормальное распределение.
Распределение с непрерывной случайной величины называется нормальным, если плотность распределения ее описывается формулой:

где  - параметры распределения.
- параметры распределения.
Функция распределения случайной величины Х, распределенной по нормальному закону:

Полученный интеграл нельзя выразить через элементарные функции, но его можно вычислить через специальную функцию:
 ,
,
называемую нормальной функцией распределения (функцией Лапласа). Эта функция неубывающая, непрерывная слева и  Математическое ожидание и дисперсия соответственно равны
Математическое ожидание и дисперсия соответственно равны 
Центральные моменты случайной величины с нормальным законом распределения вычисляются через следующие рекуррентные соотношения:

поскольку  то нечетные центральные моменты равны нулю, а четные центральные моменты равны:
то нечетные центральные моменты равны нулю, а четные центральные моменты равны: 
Коэффициенты ассиметрии и эксцесса для нормального закона распределения равны нулю:

так как они характеризуют скошенность и крутизну исследуемового закона распределения по сравнению с нормальным.
Вероятность попадания случайной величины 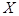 , подчиненной нормальному закону распределения, на заданный интервал
, подчиненной нормальному закону распределения, на заданный интервал  , определяется следующим образом:
, определяется следующим образом:

или
 функция Лапласа.
функция Лапласа.
Вероятность заданного отклонения вычисляется по формуле:
 или
или
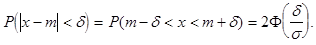
Интервалом практически возможных значений случайной величины  , распределенной по нормальному закону , будет интервал
, распределенной по нормальному закону , будет интервал 
Лекция 7-8. Предельные теоремы и законы больших чисел
Все законы вероятности получены из практики, то есть из наблюдений за массовыми случайными явлениями. Массовые случайные явления проявляются в статистической совокупности.
Было замечено, что при определенных условиях массовые случайные явления порождают величину неслучайную, которая подчиняется вполне определенным закономерностям. Все полученные соответствующие теоремы и образуют теоремы закона больших чисел, в которых приведены условия, когда среднее значение случайных величин стремится к величине не случайной. Таким образом, закон больших чисел – это совокупность теорем, в которых приведены условия, при которых последовательность случайных величин подчиняется определенным закономерностям, то есть стремится к величине неслучайной.
Неравенство Чебышева:
Теорема: Вероятность того, что случайная величина 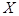 отклоняется от своего математического
отклоняется от своего математического
ожидания на величину не меньше  , ограничена сверху величиной
, ограничена сверху величиной  , где
, где  -
-
положительное действительное число:
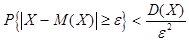 или
или 
|
из
5.00
|
Обсуждение в статье: Дискретные случайные величины |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

