 |
Главная |
Дисциплина «Обыкновенные дифференциальные уравнения.»
|
из
5.00
|
1. Дифференциальное уравнение, его порядок, решение. Поле направлений, изоклины, интегральные кривые.
2. Формулировка теоремы о существовании и единственности решения задачи Коши для уравнения первого порядка. Огибающая. Уравнение Клеро, его общее и особое решение.
3. Задача Коши для уравнения 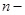 го порядка. Формулировка теоремы о существовании и единственности решения. Однородные линейные уравнения
го порядка. Формулировка теоремы о существовании и единственности решения. Однородные линейные уравнения 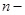 го порядка. Свойства решений.
го порядка. Свойства решений.
4. Линейная зависимость и независимость функций. Определитель Вронского и его свойства.
5. Фундаментальная система решений, её существование. Общее решение однородного линейного уравнения 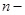 го порядка.
го порядка.
6. Неоднородное линейное уравнение  го порядка, его общее решение. Метод вариации постоянных.
го порядка, его общее решение. Метод вариации постоянных.
7. Линейные уравнения второго порядка с постоянными коэффициентами (однородные и неоднородные). Уравнение Эйлера.
8. Решение дифференциального уравнения в виде суммы ряда.
9. Уравнение Бесселя и функции Бесселя.
10. Свойства функций Бесселя нулевого и первого порядка.
Дисциплина «Дифференциальные уравнения с частными производными»
1. Линейные пространства, примеры. Скалярное произведение и норма в линейном пространстве. Неравенство Коши–Буняковского.
2. Ортогональность. Примеры ортогональных систем. Линейная независимость ортогональных функций.
3. Разложение функций по ортогональной системе. Коэффициенты Фурье. Минимальное свойство коэффициентов Фурье. Неравенство Бесселя и равенство Парсеваля.
4. Тригонометрические ряды Фурье. Вычисление коэффициентов. Формулировки теорем о сходимости.
5. Вывод одномерного уравнения теплопроводности. Постановка краевых задач для этого уравнения.
6. Метод сеток для решения первой краевой задачи для уравнения теплопроводности. Явная и неявная схемы.
7. Разделение переменных в одномерном уравнении теплопроводности. Основная лемма Фурье.
8. Задача Штурма–Лиувилля. Свойства собственных значений и собственных функций. Формулировка теоремы Стеклова.
9. Решение первой краевой задачи для уравнения теплопроводности методом Фурье.
10. Уравнение теплопроводности, задача без начальных условий. Температурные волны в почве.
11. Оператор Лапласа в полярных координатах. Решение методом Фурье задачи Дирихле для уравнения Лапласа в круге. Интеграл Пуассона.
12. Решение методом Фурье задачи о колебании закреплённой струны.
13. Задача Коши для одномерного волнового уравнения и её решение методом Даламбера.
14. Функции  и
и  . Ортогональность системы
. Ортогональность системы  . Норма функции
. Норма функции  . Использование функций Бесселя для решения краевых задач в цилиндрической области.
. Использование функций Бесселя для решения краевых задач в цилиндрической области.
|
из
5.00
|
Обсуждение в статье: Дисциплина «Обыкновенные дифференциальные уравнения.» |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

