Дисциплина «Математический анализ»

Множества и операции над ними. Функции.

Множество действительных чисел. Модуль числа.

Окрестности. Бином Ньютона, неравенство Бернулли.

Комплексные числа, их сложение и умножение. Тригонометрическая форма комплексного числа. Теорема Муавра-Лапласа. Корень n-ой степени из комплексного числа.

Верхние и нижние грани. Стягивающиеся отрезки. 

Конечные, счётные и несчётные множества.

Предел последовательности. Бесконечно малые последовательности. Арифметические свойства предела. Предельный переход в неравенствах. Предел монотонной ограниченной последовательности. Число .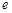

Теорема Больцано-Вейерштрасса.

Критерий Коши существования предела последовательности. Предельные точки множества. Эквивалентность определений предела по Коши и по Гейне. Свойства предела функции, бесконечно малые функции. Критерий Коши существования предела функции. Односторонние пределы.

Предел монотонной функции, предел композиции.

Непрерывность, точки разрыва. Свойства непрерывных функций.

Непрерывность элементарных функций. Символы . Вычисление замечательных пределов.          Промежуточные значения непрерывной на отрезке функции. Ограниченность непрерывной на отрезке функции.   Равномерная непрерывность. Теорема Кантора.

   Непрерывность монотонной функции, обратная функция и её непрерывность.

Производная, её основные свойства, дифференцируемость. Производные элементарных функций. Производная обратной функции.  Производная сложной функции. Производная функции, заданной параметрически.

Дифференциал. Инвариантность формы первого дифференциала. Геометрический смысл производной и дифференциала. Производные и дифференциалы высших порядков.

   Теоремы Ферма, Ролля. Необходимые условия экстремума.                                                         

Теоремы Лагранжа и Коши. Связь монотонности и знака производной. Критерий постоянства функции на интервале.

   Формула Тейлора с остаточным членом в форме Лагранжа.

 Формула Тейлора с остаточным членом в форме Пеано.    Правила Лопиталя.

    Монотонность функции. Достаточные условия экстремума функции.

 Выпуклость графика функции. 

Общие правила интегрирования: интегрирование по частям, интегрирование подстановкой. Таблица неопределённых интегралов.

Интеграл Римана. Необходимое условие интегрируемости.

Суммы Дарбу и их свойства. Критерий интегрируемости. Классы интегрируемых функций.

Интегрируемость по подотрезкам, аддитивность, линейность . Интегрируемость кусочно непрерывной функции..

Свойства определённого интеграла. Интеграл с переменным верхним пределом. Вычисление определённых интегралов по основной формуле интегрального исчисления (формуле Ньютона-Лейбница).

Приложения интеграла: объём тела. длина дуги кривой и площадь

поверхности вращения.

Метрические пространства, пространство . Открытые, замкнутые, компактные множества.

Полные метрические пространства, полнота . Теорема Больцано-Вейерштрасса для компактов метрических пространств.

 Функции нескольких переменных, отображения, их пределы и непрерывность.

Дифференцируемость функций нескольких переменных. Частные производные. Достаточные условия дифференцируемости функции.

Дифференциал. Производная сложной функции. Инвариантность формы первого дифференциала.

Касательная плоскость. Производная по направлению. Градиент.

Производные и дифференциалы высших порядков. Равенство смешанных производных.

Формулы Тейлора с остаточными членами в форме Лагранжа и Пеано. Экстремумы функций нескольких переменных. Достаточное условие локального экстремума.

Неявная функция. Уравнения касательной плоскости и нормали к заданной неявно поверхности. Теорема о неявном отображении. Обратное отображение. Матрица Якоби композиции.

Условный экстремум.

Числовые ряды. Критерий Коши сходимости. Свойства сходящихся рядов.

Ряды с неотрицательными членами. Теоремы сравнения. Признаки Даламбера, Коши. Метод выделения главной части.

Абсолютная сходимость. Свойства абсолютно сходящихся рядов.

Условная сходимость. Теорема Лейбница.

Равномерная сходимость функциональной последовательности,

ряда, sup-критерий, критерий Коши. Признак Вейерштрасса.

Непрерывность суммы равномерно сходящегося ряда из непрерывных функций. Почленное интегрирование и дифференцирование функциональной последовательности, ряда. Полнота пространства C[a,b].

Несобственные интегралы. Формулы Ньютона- Лейбница, замены переменных и интегрирования по частям. Линейность несобственного интеграла, интегрирование неравенств. Критерий Коши сходимости несобственных интегралов. Теоремы о сравнении для несобственных интегралов от неотрицательных функций. Интегральный признак Коши сходимости числовых рядов.

Абсолютно сходящиеся интегралы. Условно сходящиеся интегралы.

Признаки Абеля и Дирихле. Главное значение несобственного интеграла.

Степенные ряды. Радиус сходимости. Непрерывность их суммы. Почленное интегрирование и дифференцирование степенных рядов. Разложение элементарных функций в степенные ряды.

 Кратный интеграл Римана по брусу, суммы Дарбу и их свойства.

Критерий Дарбу интегрируемости. Множества меры нуль по Лебегу и их свойства. Критерий Лебега интегрируемости функции на брусе.

Допустимые множества, интеграл Римана по множеству, мера Жордана ограниченного множества. Критерий Лебега интегрируемости на измеримом множестве. Свойства интеграла Римана, интеграл и неравенства. Вычисление кратного интеграла сведением к повторным. Замена переменных в кратном интеграле Римана(без доказательства) . Цилиндрические и сферические координаты. Кратные несобственные интегралы.

Собственные интегралы, зависящие от параметра, их непрерывность, дифференцирование и интегрирование.

  Несобственные интегралы, зависящие от параметра. Равномерная сходимость. Критерий Коши, признак Вейерштрасса. Непрерывность, дифференцируемость и интегрируемость по параметру несобственных интегралов. Признаки Абеля и Дирихле

Тригонометрические ряды. Тригонометрические ряды Фурье, их сходимость. Комплексная форма тригонометрического ряда Фурье.

Пространство L₂(a,b). Сходимость в смысле среднего квадратичного

Ортогональные системы функций. Ряды Фурье функций из L₂(a,b).

 Минимальное свойство коэффициентов Фурье. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота тригонометрической системы функций.

Кривые. Ориентация кривой, касательная к кривой. Поверхности. Касательная плоскость и нормаль к поверхности.

Криволинейный интеграл 1-го и 2-го рода. Физический смысл криволинейного интеграла 2-го рода. Формула Грина. Потенциальные векторные поля.

Площадь поверхности. Поверхностные интегралы 1-го и 2-го рода. Физический смысл поверхностного интеграла 2-го рода. Формула Гаусса- Остроградского. Дивергенция векторного поля и её физический смысл.

Формула Стокса. Ориентация кусочно-гладкой поверхности.

Преобразование Фурье. Эйлеровы интегралы