 |
Главная |
Построение линий влияния продольных сил в стержнях фермы
Линия влияния N1
Используя статический метод, стремимся свести построение Л.В. к типовым задачам ( см. п. 2.3.1, с. 76 ). Поскольку ферма многодисковая и имеет главную и две второстепенные части ( см. рис. 2.32 ), построение линии влияния начинаем с той части, в ко-торой расположен стержень с искомым усилием ( для N1 – ГЧ ). Сразу применить типовые Л.В. из представленных на рис. 2.28 не удаётся, так как решётка рассчитываемой фермы в левой половине ГЧ является сложной ( двухраскосной ). Поэтому действуем аналогично тому, как это сделано в примере на с. 78. Определяем усилие N1 тем же способом совместных сечений, что и в рас-
чёте на постоянную нагрузку – используем основное сечение I – I ( рис. 2.39, а ) при ЕПН и дополнительно учитываем NuB . Не принимая во внимание особенности узловой передачи нагрузки по нижнему поясу ( они будут учтены в последнюю очередь ), замечаем, что NuB = 0 при расположении груза F = 1 во всех узлах, кроме t и u. Поэтому сначала строим Л.В. N1 , игнорируя элементы tu и uB ( по схеме рис. 2.39, б, где решётка – простая раскосная), как типовую для стержня пояса, усилие в котором рационально отыскивается способом моментной точки: между опо-рами A и B линия влияния имеет вид треугольника с вершиной под моментной точкой K1 ( рис. 2.39, в ); характерная ордината – по рис. 2.28, ж (плечо h1 = 3,795 м уже определено ранее – см. с. 87).
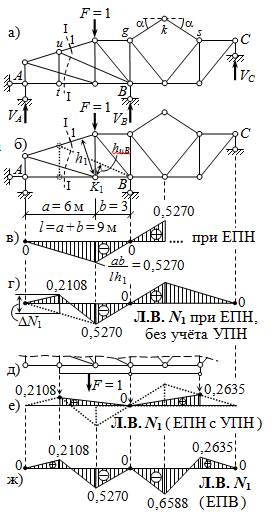
Рис. 2.39
 Далее рассматриваем загружение единичной силой узлов t и u: по схеме рис. 2.36, д при F = 1 имеем NuB = –1∙ cos q / sin (q + j)= = –1,3416 . Поправка к N1 за счёт влияния NuB определяемая из
Далее рассматриваем загружение единичной силой узлов t и u: по схеме рис. 2.36, д при F = 1 имеем NuB = –1∙ cos q / sin (q + j)= = –1,3416 . Поправка к N1 за счёт влияния NuB определяемая из
уравнения моментов 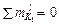 , составляет DN1= – NuB ∙ huB / h1 =
, составляет DN1= – NuB ∙ huB / h1 =
= – (–1,3416) ∙1,3416 / 3,795 = 0,4743 – используем её для получения ординаты Л.В. под узлами t и u ( рис. 2.39, г ). Достраиваем линию влияния в пределах второстепенной части ВЧ1 , как пря-мую, по двум ординатам – общей на границе ВЧ1 и ГЧ и равной 0 под опорой С ( при расположении силы F = 1 в опорном узле ни один стержень фермы не работает ). Учитывая узловую передачу нагрузки по нижнему поясу ( рис. 2.39, д ) как описано в п. 1.4.3,
получаем линию влияния усилия N1 в случае езды понизу ( рис. 2.39, е ).
Линия влияния при езде поверху при расположении под- вижного груза F = 1 во всех узлах, кроме верхнего k ( на сáмой второстепенной части – рис. 2.39, а ) совпадает с представленной на рис. 2.39, г, так как при переносе F = 1 по линии действия с нижнего пояса на верхний не изменяются ни реакции опор, ни уравнения равновесия левой отсечённой части стержня и выделенного узла u. Для определения ординаты Л.В. под узлом k вы-
резаем этот узел и находим Nkg = Nks = – 0,5 / sin a = – 0,9014 с про-
екциями Yks = – 0,5 и Xks = – 0,75. Далее, действуя так же, как в рас-чёте на постоянную нагрузку, вычисляем опорную реакцию VC =
= ( 0,5 ∙ 3 + 0,75 ∙ 4 ) / 6 = 0,75, затем из уравнения S mB = 0 для фермы в целом: VA = ( 0,75 ∙ 9 – 1 ∙ 3 ) / 9 = 0,4167. Наконец, для левой
части: 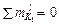 , откуда N1 = – 0,4167 ∙ 6 / h1 = – 0,6588. Линия вли-
, откуда N1 = – 0,4167 ∙ 6 / h1 = – 0,6588. Линия вли-
яния N1 при езде поверху приведена на рис. 2.39, ж.
Линия влияния N2
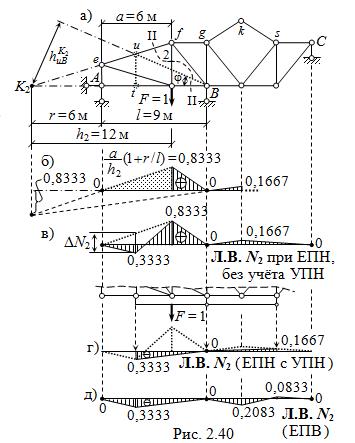
Построение Л.В. N2 выполняем в том же порядке, что и Л.В. N1 . Начинаем с части, которой принадлежит стержень с ис-комым усилием. Условно исключив элементы tu и uB, строим ли-нию влияния при езде понизу, используя схему, представленную на рис. 2.40, а. Разделив ферму сечением II – II, выбираем момент-ную точку K2 в месте пересечения продолжений осей рассечённых стержней поясов. Вновь применяя правило использования моментной точки для выявления формы линии влияния ( см. с. 77 ) получаем «заготовку» Л.В. N2 как типовую по рис. 2.28, з – показана на рис. 2.40, б, где пунктиром обозначен участок, на котором нужно внести поправку от загружения узлов t и u.
Эту поправку находим из уравнения 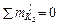 :
:
DN2 = NuB∙ 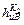 / h2 ,
/ h2 ,
где NuB = – 1,3416 ( найдено ранее на с. 92 );
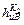 = 15 м ∙ sin j = 6,708 м; DN2 = – 0,75.
= 15 м ∙ sin j = 6,708 м; DN2 = – 0,75.
Линия влияния усилия N2 при езде понизу, без учёта узловой передачи нагрузки, с продолжением на второстепенную часть ВЧ1 , показана на рис. 2.40, в, а с учётом УПН – на рис. 2.40, г.
При перемещении единичного груза по верхнему поясу линия влияния на участках узлами e и u , а также s и C – такая же, как при езде понизу; между узлами f и g – продолжение влево правой прямой ( с ординатами 0 и 0,1667 ) на рис. 2.40, б; между узлами u и f – соединительная прямая, совпадающая с продолжением правой прямой. Особо нужно рассмотреть загружение силой F = 1 узла k, принадлежащего сáмой второстепенной части ВЧ2 . Используя значение реакции VA = 0,4167 от указанного загружения, найденное при построении Л.В. N1
|
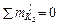 получаем N2 = – 0,4167 ∙ r / h2 =
получаем N2 = – 0,4167 ∙ r / h2 =
Линия влияния N3
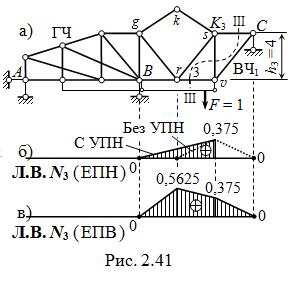
При перемещении подвижного груза F = 1 по главной части ( рис. 2.41, а ) от левого края фермы до узла g по верхнему поясу и до узла r по нижнему поясу усилие N3 в стержне второстепенной части, выявленное сечением III – III, равно 0.
При движении силы F = 1 по ВЧ1 линия влияния N3 в стержне пояса строится как типовая по рис. 2.28, ж: между точками r и C – треугольная, с вершиной подмоментной точкой K3 и нулевыми ординатами под r и C, единая при езде поверху и понизу ( без учёта узловой передачи нагрузки ), но при ЕПВ она состоит из левой прямой от r до s и соединительной между s и C, а при ЕПН – из правой прямой от v до s и соединительной между r и v. Линия влияния N3 при езде понизу предcтавлена на рис. 2.41, б. Ординату её вер-шины при грузе F = 1 в узле v ( соответственно VC = 0,5 ) вычисляем решением уравнения равновесия правой отсечённой части
фермы 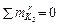 : N3 = 0,5 ∙ 3 м / h3 = 0,375.
: N3 = 0,5 ∙ 3 м / h3 = 0,375.
Для построения Л.В. N3 при езде поверху дополнительно рассматриваем положение силы F = 1 в узле k. Вновь используя ранее найденную реакцию VC = 0,75 ( см. с. 92 ), из того же урав-
нения 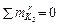 получаем N3 = 0,5625 и по четырём ординатам, из
получаем N3 = 0,5625 и по четырём ординатам, из
которых две – нулевые, строим линию влияния усилия N3 при езде поверху ( рис. 2.41, в ).

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

