Линии влияния силовых факторов в трёхшарнирных системах

    Линии влияния опорных реакций и внутренних усилий в некотором сечении внешне распорной ТШС являются типовыми^*) вследствие единообразия структуры ( при наличии только цилинд-рических шарниров ). Для системы с опорами на одном уровне (рис. 2.61, а) типовые Л.В. получаются из следующих соображений:

Ø линии влияния вертикальных составляющих V_A и V_B реакций опор арки совпадают с соответствующими Л.В. опорных реакций простой балки ( рис. 2.7, между точками A и B );

Ø линия влияния распора Н имеет вид треугольника с вершиной под ключевым шарниром С ( рис. 2.61, б ); ордината находится из ( 2.23 ) при грузе F = 1, расположенном в С ( на балке – в С₀ );

^*)  Для внутренне распорных ТШС с затяжкой также существуют анало-

гичные типовые Л.В.

Ø линии влияния изгибающего момента, поперечной и продольной сил в сечении K с абсциссой x_K , ординатой y_K и углом наклона  q_K  получаются статически на основании  выражений ( 2.20 ) – ( 2.22 ) при x = x_K , y (x) = y (x_K) 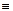y_K , q (x) = q (x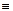_K) q_K :

 

Л.В. M_K  = Л.В. M_{0, K}  – y_K ∙ Л.В. H ;                ( 2.27 )

Л.В. Q_K = cos q_K ∙ Л.В. Q_{0, K} – sin q_K ∙ Л.В. H;       ( 2.28 )

Л.В. N_K = – [ sin q_K ∙ Л.В. Q_{0, K} + cos q_K ∙ Л.В. H ],    ( 2.29 )

где Л.В. M_{0, K} и Л.В. Q_{0, K}

для сечения балки с координатой x = x_K – типовые Л.В. M₁ и Л.В. Q₁ по рис. 2.7 с заменой   a и b    соответственно на x_K и l – x_K .

  Характерные орди

292.3

наты типовых линий  влияния на рис. 2.61:                             

 

302.3

312.3

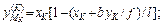
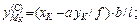
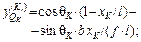
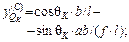
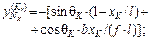
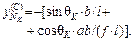
    Указанные ординаты можно находить прямым вычислением силовых факторов в ТШС при двух положениях подвижного груза F = 1 – над сечением K и в шарнире С.          

 

 

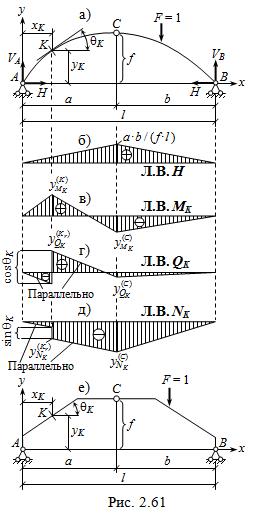
    Линии влияния ре

акций и усилий в трёхшарнирной раме – такие же, как для арки. Например, если рама на рис. 2.61, е имеет такие же размеры l, a, b и f , что и арка ( рис. 2.61, а ), то в случае совпадения параметров x_K , y_K и q_K сечения K рамы и арки линии влияния M_K, Q_K и N_K – одинаковые для обеих ТШС.

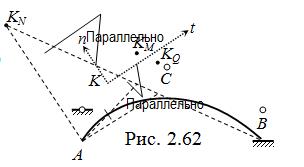
Примечания : 1. Для контроля положения нулевых точек средних прямых линий влияния усилий  в  сечении  K   можно  использовать моментные точки,  нахождение  которых показано на рис. 2.62 ( их  статический  смысл подробно объяснён,  в частности, в [ 2 ] ).  Нулевые точки линий влияния M_K , Q_K  и N_K  располагаются соответственно  под   моментными  точками  K_M , K_Q и K_N . Графические построения для отыскания указанных точек, конечно, следует выполнять со строгим соблюдением масштаба.

 

 

 

342.3

 2. Модели линий влияния силовых факторов в ТШС можно получать кинематическим методом ( см. [ 4 ] ). Заметим, что в этом случае мгновенные центры вращения диска KC при построении линий влияния M_K , Q_K и N_K совпадают с моментными точками K_M , K_Q и K_N .

  Комбинированной называется геометрически неизменя-емая система, состоящая из различных по характеру своей работы частей, совместно участвующих в восприятии задан-ных воздействий.

352.3

    В состав комбинированной системы ( КС ) могут входить части в виде балок, рам, арок, ферм и отдельных стержней с прямыми, кривыми или ломаными осями. Внутренние усилия в любом из фрагментов КС определяются известными приёмами для системы или элемента соответствующего типа, поэтому основной задачей расчёта КС является определение реакций опор и внутренних связей между её частями.

 

                                                                      

    Если при выполнении структурного ( качественного ) анализа удаётся представить образование комбинированной системы с помощью типовых способов соединения дисков ( см. п. 1.1 ), то это – комбинированная система с простой структурой. Её расчёт выполняется в порядке,

обратном последовательности синтеза системы.

 

 

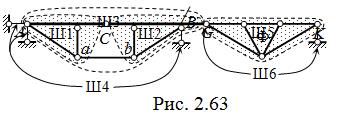
        Например, образование КС, изображённой на рис. 2.63,

выполняется последовательными шагами: Ш 1, Ш 2, Ш 3 – создание дисков; Ш 4 – прикрепление укрупнённого диска к «земле» ( получается главная часть системы ); Ш 5 – об-разование диска Ф (при узловых нагрузках – фермы); Ш 6 – соединение  диска Ф с главной частью и «землёй» ( возникает второстепенная часть ).

    Расчёт комбинированной системы рационально выполнять в следующем порядке: расчётный шаг РШ 1 Ш 6 – определение реакций связей второстепенной части (опоры K и шарнира G ) и вычисление уси-лий в ней ( РШ 2 Ш 5 ); третий шаг – РШ 3  Ш 4 – нахождение реакций опор A и B главной части; РШ 4 Ш 3 – разделение главной части по шарниру C и связи ab с определением их реакций; РШ 5 Ш 2 и РШ 6 Ш 1 – вырезание узлов a и b, вычисление продольных сил в вер-тикальных и наклонных стержнях. Далее – расчёт внутренних усилий в балочных элементах AC и CG главной части.

     Комбинированные системы со сложной структурой, образование которых не сводится к последовательному применению типовых способов соединения дисков, в данных методических указаниях не рассматриваются ( об этом классе КС см. в [ 1 – 5 ]  ).                 

2.4.2. Содержание задания

y

        

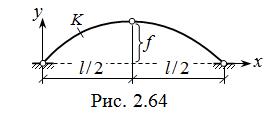
Задача 1. Для трёхшарнирной арки ( рис. 2.64 ) требуется:

    1.1. Определить реакции опор от заданной постоянной нагрузки.

    1.2. Вычислить изгибающий момент, поперечную и продольную силы в заданном сечении K арки.

 

 

    1.3. Подготовить исходные данные и выполнить компью-терный расчёт по программе ARKA. По полученным данным построить эпюры M,  Q и N в арке ( на горизонтальных осях, с шагом не менее l / 8 ).

       1.4. Для сравнения построить балочные эпюры M₀ и Q₀ .

    1.5. Построить линии влияния распора и усилий в сечении K, выполнить их загружение постоянной нагрузкой и сопоставить полученные значения с результатами расчётов по п. 1.1 и 1.2.

    1.6. Составить матрицу влияния распора и силовых факторов в сечении K и вектор расчётных узловых нагрузок; найти S.

    1.7. Сформировать конечно-элементную модель арки и составить матрицы коэффициентов A и свободных членов B_F уравнений статики ( см. с. 106 – 107 ). Определить силовые факторы S.

    1.8. Факультативно: выполнить расчёт по программе ARKA  с иным, чем в основном решении, очертанием оси арки и сравнить результаты ( эпюры ).

 

    Указание: в вычислениях использовать следующие сведения о геометрии арок с различными очертаниями осей: 

Очертание оси арки	Уравнение оси	Угол наклона сечения
Парабола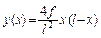
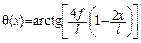
Дуга окруж- ности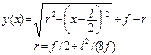
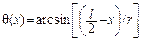
Верхняя половина эллипса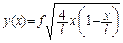

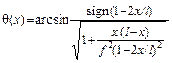
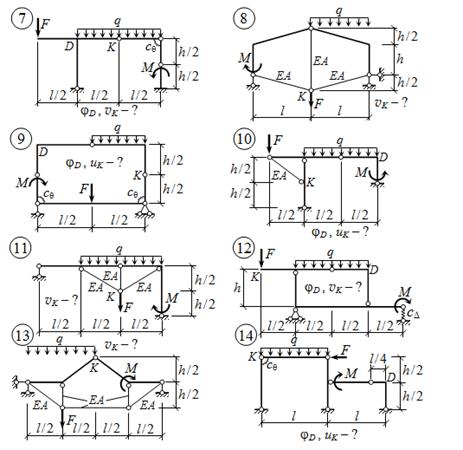
    Задача 2. Для статически определимой рамы или комбинированной системы:

    2.1. Выполнить кинематический анализ и определить последовательность расчёта системы.

    2.2. От действия заданной нагрузки

– определить реакции опор и внутренних связей;

– построить эпюры внутренних силовых факторов;

– методом Максвелла – Мора найти угол поворота j_D узла D и указанное  линейное перемещение  точки K  ( u_K – горизонтальное, v _K – вертикальное ); в комбинированной системе – только линейное перемещение.

    2.3. Факультативно: сформировать конечно-элементную модель системы и составить матрицы коэффициентов и свободных членов уравнений статики. Решение – по усмотрению.

2.4.3 . Варианты исходных данных

а) для трёхшарнирной арки

 

 

№ вари- анта	l , м	q , кН/м	F1 , кН	F2 , кН	M , кН ∙м	№ вари- анта	l , м	q , кН/м	F1 , кН	F2 , кН	M , кН ∙м
1	48	10	20	36	24	6	40	12	24	16	44
2	64	8	40	32	48	7	32	18	40	30	20
3	40	16	24	30	30	8	24	20	30	24	42
4	48	12	30	40	36	9	48	15	36	40	30
5	32	15	18	24	40	10	64	10	50	32	56

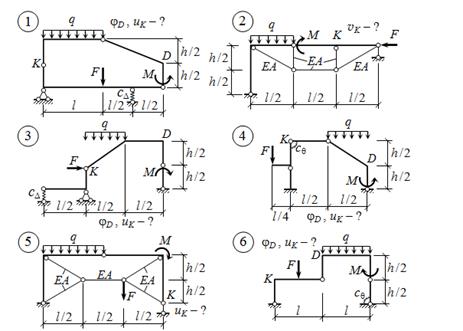
Схемы нагрузок и очертания осей трёхшарнирных арок

 

 

 

№№ схем	1 – 6	7 – 12	13 – 18	19 – 24
f / l	1 / 5	1 / 4	1 / 8	1 / 4

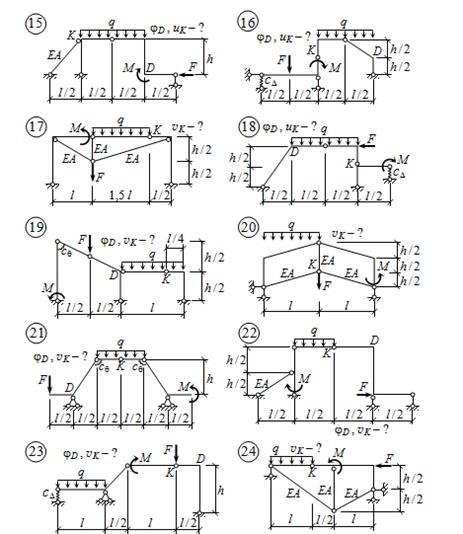
б) для рам и комбинированных систем

 

 

№ вари- анта	l , м	h , м	EI2 EI1	q , кН/м	F , кН	M , кН ∙ м	№ вари- анта	l , м	h , м	EI2 EI1	q , кН/м	F , кН	M , кН ∙ м
1	4	3	3	12	25	20	6	4	4	1,5	15	20	16
2	6	4	2	16	20	30	7	8	5	4	10	25	48
3	4	4	2	10	30	24	8	4	2	3	18	15	20
4	8	6	3	8	20	40	9	6	3	2	10	25	30
5	6	5	2	12	24	36	10	4	3	1,5	16	20	24

EI₁ – жёсткость сечения при изгибе вертикальных стержней, EI₂ – для го-

EA = 36 l – 2 EI1 ;  cD = 3EA /   l;  cq = 4EI1 / l .

ризонтальных и наклонных элементов (кроме обозначенных типом EA);