Формирование системы уравнений статики по конечно-элементной модели

    Расчётная схема элементов и узлов системы, составленная по алгоритму, изложенному и проиллюстрированному примером в п. 1.3.1 на с. 13 – 18, представлена на рис. 2.91.

       Рекомендации по рациональной нумерации эле-ментов и узлов даны на с. 127.

       В вектор искомых силовых факторов не включаем заведомо равные 0 моменты в сечениях у шарниров; вследствие этого уравнения третьей  группы ( см. с. 18 ) из системы ( 1.3 ) исключаются. Не записываются в явном виде также уравнения равновесия элементов 3, 5, 6, 8 и 9, испытывающих растяжение или сжатие. Для шарнирных узлов 2, 3, 5, 6, 8 и 9 составляем по два уравнения – в проекциях сил на оси x и y, а для жёстких узлов 1, 4 и 7 – по три. Таким образом, имеем:

S = [ M_b1 Q_b1 N_b1 Q_e1 N_e1 M_b2 Q_b2 N_b2 Q_e2 N_e2 N_c3 Q_b4 N_b4 M_e4 Q_e4 N_e4 N_c5 N_c6 M_b7 Q_b7 N_b7 Q_e7 N_e7 N_c8 N _c9 Q_b10 N_b10 M_e10 Q_e10 N_e10 M_b11 Q_b11 N_b11 Q_e11 N_e11 V_A H_A V_B V_G ] ^т – 39  компонентов. Матрица  коэффициентов  уравнений  равновесия  элементов 1, 2, 4, 7, 10, 11:

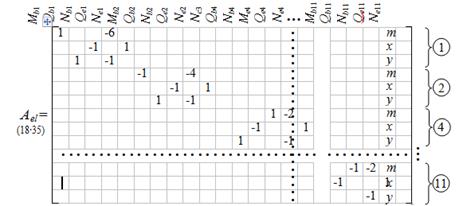
    Матрица коэффициентов второй группы уравнений ( 1.3 ) – для узлов:

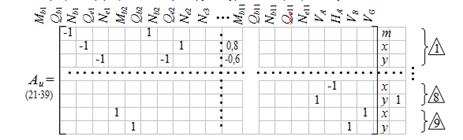
    Вектор свободных членов уравнений равновесия ( учёт нагрузки ):

B_F = [ 0  0  0  -96  0  -48  -24  0  -24  0  0  0  -60  -20  0  0  0  0  0  0  0  0  0  0  0  -50

        0  0  0  -20  0  0  0  0  0  0  0  0  0 ] ^т.

         Значения S, которые даёт решение системы ( 1.3 ), практически совпадают с най-денными в основном расчёте.

2.4.7. Контрольные вопросы по теме 2.4

1. Что такое трёхшарнирная система (ТШС)? (100)

  2. Основные типы трёхшарнирных систем. (100)

   3. Что такое трёхшарнирная арка, трёхшарнирная рама? (101 )

  4. Требования к расположению связей в ТШС. (100)

5. Можно ли в трёхшарнирной системе выделить главную и второстепенную части?

6. Порядок определения реакций связей в трёхшарнирной распорной системе при произвольном взаимном расположении шарниров. (101)

7. Что называется распором? (100)

8. От чего зависит распор трёхшарнирной системы? (105)

  9. Рациональный порядок определения реакций связей в ТШС при расположении ключевого и одного из опорных шарниров на одной вертикали (или горизонтали). (103)

10. Порядок определения реакций связей в трёхшарнирной системе с затяжкой. (103)

11. Каков характер работы незагруженной прямолинейной затяжки? (100)

12. Как определяется продольная сила в прямолинейной незагруженной затяжке? (103)

   13. Какие усилия возникают в произвольном сечении трёхшарнирной арки или рамы? (104)

14. Как определяются вертикальные составляющие опорных реакций трёхшарнирной системы с опорами на одном уровне в случае вертикальной нагрузки? (104)

15. Как отыскивается распор трёхшарнирной арки; как он зависит от стрелы подъёма? (105) Почему ключевой шарнир трёхшарнирной системы целесообразно располагать в её верхней точке? (106)

16. Формулы для внутренних силовых факторов (изгибающего момента, поперечной и продольной сил) в произвольном сечении трёхшарнирной системы (арки, рамы) от вертикальной нагрузки. (104)

17. Изгибающие моменты в арке больше или меньше моментов в балке того же пролёта при той же вертикальной нагрузке? Почему? (105)

18. Дифференциальные уравнения равновесия элемента криволинейного стержня. (105)

 19. Особенности очертания эпюр ВСФ в трёхшарнирных арках. (105)

 20. Как используются дифференциальные зависимости между усилиями в криволинейном стержне для построения и проверки эпюр ВСФ в арке? (105)

 21. Какую особенность имеют эпюры Q и N в арке или раме в месте приложения сосредоточенной силы F ? (105)

 22. Чему равны поперечная и продольная силы в сечении в вершине арки с опорами на одном уровне от действия вертикальной нагрузки?   (самостоятельно)

23. Что такое трёхшарнирная система с рациональным очертанием оси? Главное свойство ТШС рационального очертания. (120)

 24. Какие усилия возникают в ТШС рационального очертания? (120)

   25. Каково рациональное очертание оси арки при равномерно распределённой по всей её длине гидростатической нагрузке? [4]

 26. Уравнение оси трёхшарнирной системы рационального очертания при вертикальной нагрузке. (121), [4]

 27. Каково рациональное очертание оси арки при равномерно распределённой по всему пролёту вертикальной нагрузке? [4] 

28. Какое очертание оси арки – параболическое или эллиптическое – выгоднее при вертикальных нагрузках, приложенных вблизи от опор?

(121)

 29. Какой вид имеет линия влияния распора трёхшарнирной системы с опорами на одном уровне? (108)

 30. Какой вид имеют типовые линии влияния внутренних усилий в произвольном сечении трёхшарнирной системы: а) изгибающего момента;  б) поперечной силы в сечении, расположенном слева (справа) от ключевого шарнира;  в) продольной силы в сечении ТШС левее (правее) ключевого шарнира? (108)

 31. Чему равны разрывы (скачки) на Л.В. Q и Л.В. N в сечении трёхшарнирной арки или рамы? (108)

 32. При каких загружениях трёхшарнирной арки равномерной времен-

ной нагрузкой в её сечениях возникают наибольшие по абсолютной величине  а) изгибающие моменты? б) продольные силы? [4]

33. Порядок расчёта составной системы с трёхшарнирными частями. (101, 8), [4]

34. Какие системы называются комбинированными? (109)

35. Как определяется рациональный порядок расчёта комбинированной системы с простой структурой? Какую роль играет при этом струк-турный анализ системы? (109)

36. В каком порядке рассчитывается система типа «шпренгельная балка»? [4]

37. Как выполняется кинематический анализ комбинированной системы со сложной структурой типа «жёсткая балка с гибкой аркой» (ЖБГА)? [4]

 38. Какова рациональная последовательность расчёта системы типа ЖБГА? [4]

39. Через какой силовой фактор удобно выражать усилия в элементах шарнирной цепи и стойках (подвесках)? Какие уравнения для этого ис-пользуются? [4]

40. Как определяются реакции связей (опорных и соединительного шарнира) балочной части комбинированной системы типа ЖБГА? [4]

41. В чём состоит аналогия между комбинированной системой типа ЖБГА и трёхшарнирной аркой при расчёте на вертикальную нагрузку? [4]

42. Как задаётся очертание оси и места расположения шарниров в арке-аналоге? [4]

43. По каким формулам вычисляются изгибающие моменты и поперечные силы в балке комбинированной системы через моменты и поперечные силы в арке-аналоге? [4]

44. Контрольные вопросы 82 – 97 к главе 1 (см. с. 45).

45. Как записывается формула Максвелла – Мора в случае определения перемещений от силового воздействия (нагрузки) в рамной системе с элементами, работающими преимущественно на изгиб? [4]

46. Каким слагаемым формулы Максвелла – Мора учитывается влияние на перемещения рамной системы деформаций растянутых/сжатых элементов (затяжек, подкосов и т. п.)? (126), [4] 

47. Если в системе есть упругоподатливые связи, то как учитывается их влияние на перемещения? (37), [4]

48. По  какой  формуле  вычисляются  перемещения  от  силового воздействия методом Максвелла – Мора в комбинированной стержневой системе с изгибаемыми и растянутыми/сжатыми элементами и упругоподатливыми связями? (132), [4]