Определение усилий в арке при очертании оси, отличном от заданного

242.3

232.3

        Значения реакций связей трёхшарнирной системы обусловлены нагрузкой, вза-имным расположением шарниров, размерами l и f , но на них не влияет форма оси арки или рамы. При этом внутренние силовые факторы в сечениях существенно зависят от очертания оси, задаваемого выражением y(x) – это видно из формул ( 2.20 ) – ( 2.22 ). Варьируя форму оси, можно получать выгодное распределение усилий в системе и даже добиваться безмоментности арки или рамы, т. е. равенства нулю моментов во всех сечениях при заданной нагрузке: M ( x ) 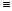0. Такая трёхшарнирная система называется системой с рациональным очертанием оси; в её сечениях возникают только продольные силы. В случае вертикальной нагрузки, когда M(x) = M₀ (x) – H ∙ y(x), условие безмоментности даёт уравнение рациональной оси: y_r(x) = M₀ (x) / H – до постоянного множителя H ^–1 = f / M_{0, C} форма оси безмоментной арки или рамы совпадает с очертанием балочной эпюры изгибающих моментов.

262.3

    При многокомпонентных нагрузках рациональная форма оси может быть трудноосуществимой в изготовлении реальных конструкций – тогда назначается одно из типовых очертаний, близкое к рациональному. Для арок можно руководствоваться следующими соображениями:

v при нагрузках, примерно равномерно распределённых по длине пролёта, целесообразно выбирать параболическое очертание;

282.3

v если нагрузки располагаются в основном в средней части пролёта, то ближе к рациональной будет синусоидальная или параболическая форма оси;

v в случае, когда нагрузки приложены преимущественно в приопорных зонах, более выгодной является арка в форме дуги окружности или половины эллипса.     

137,61

    Для арки с нагрузками, заданными в рассматриваемом примере ( см. рис. 2.66 ), выполним расчёт внутренних усилий при эллиптическом очертании оси. Используя программу ARKA, в исходных данных изменяем только один компонент – описание формы оси. Результаты компьютерного счёта представлены в виде эпюр M, Q, N на рис. 2.69. Там же для сравнения штриховыми линиями показаны усилия в круговой арке, найденные в основном решении задачи.

 

 

Эпюры изгибающих моментов в двух арках, различающихся только формой оси, сильно отличаются друг от друга, во-первых, по общему виду ( в круговой арке моменты все положительные, в эллиптической – разнозначные ), а во-вторых – по наибольшим абсолютным значениям моментов ( в эллиптической – почти в 1,5 раза меньше ). Продольные силы в двух арках на большей части длины почти одинаковые; значительные расхождения только вблизи опор, причем меньшие N – также в эллиптической арке.

    Читателю предлагается самостоятельно убедиться в том, что в арке с осью по параболе 2-й степени или синусоиде, изгибающие моменты существенно больше, чем при двух рассмотренных выше очертаниях оси – по окружности и эллипсу.