 |
Главная |
Пример расчёта плоской составной рамы
Требуется рассчитать раму, изображённую на рис. 2.70, согласно указаниям, приведённым на с. 111. Принять EA = 0,5 м – 2 EI.
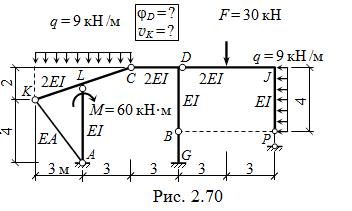
Кинематический анализ
1. Проверка условия
W < 0, где W = 3D –
– (3П + 2H + C + C0):
D = 5 ( AL, KC, CDB,
BG и DJP ); П = 0;
H = 4; С = 1 (AK); С0 = 6;
W = 3∙5 – (0 + 2∙4 + 1 + 6) = 0.
2. Структурный анализ: BG + «земля» = ГНС1; AK + KC + LA = D1 (трёхшарнирный); ГНС1 + BDC + D1 = ГНС2 (трёхшарнирная сис-тема); ГНС2 + DJP = ГНС. Все связи наложены правильно.
Определение внутренних усилий в раме и построение их эпюр
Как видно из структурного анализа, рама является составной системой с главной частью BG и второстепенными AKLCDB (ВЧ1) и DJP (ВЧ2). Порядок расчёта рамы: ВЧ2  ВЧ1
ВЧ1  ГЧ.
ГЧ.
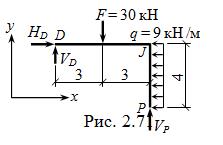
|
S mD = 0  VP = (F∙3 + q∙4∙2) /6 = 27 кН;
VP = (F∙3 + q∙4∙2) /6 = 27 кН;
S x = 0  HD = q∙4 = 36 кН;
HD = q∙4 = 36 кН;
S y = 0  VD = F – HD = 3 кН.
VD = F – HD = 3 кН.
Эпюры внутренних силовых факторов в ВЧ2 даны на рис. 2.72.
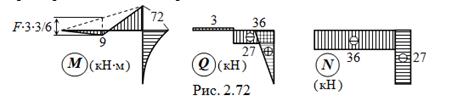
Замечание. Эпюра M может быть построена без определения опорных реакций: на участке JP и дополнительная на DJ от нагрузки F – как типовые из табл. 1.2. Эпюра Q – по M ( см. с. 19 – 20 ), N – из условий равновесия узла J.
n, - 20 з табл. от нагрузки Аления опорных реакций далее рассматриваем трёхшарнирную второстепенную часть ВЧ1 ( рис. 2.73, а ). Шарниры A и B находятся на разных уровнях, и при этом ключевой шарнир С
не располагается ни на общей вертикали, ни на общей горизонтали с каким-либо из опорных шарниров. Поэтому реакции связей определяем по алгоритму, изложенному на с. 101 –103. Кроме нагрузок, приложенных к ВЧ1, учитываем давление, которое на неё оказывает ВЧ2 ( направления HD и VD – противоположные показанным на рис. 2.72 ).
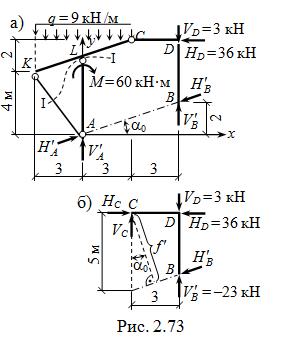
S mA = 0 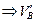 = (VD∙ 6 + M – HD∙ 6) /6 = – 23 кН;
= (VD∙ 6 + M – HD∙ 6) /6 = – 23 кН;
S mB = 0 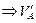 = (HD∙ 4 + q ∙6∙6 – M ) /6 = 68 кН;
= (HD∙ 4 + q ∙6∙6 – M ) /6 = 68 кН;
S x = 0 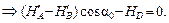
|
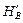 рассматриваем
рассматриваем
правую часть ТШС ( рис. 2.73, б) и записы-
ваем уравнение равновесия моментов относительно точки С:
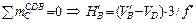 , где f ' = 5 м ∙cos a0 ( рис. 2.73, б );
, где f ' = 5 м ∙cos a0 ( рис. 2.73, б );
получаем 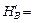 –15,6 / cos a0 . Из третьего уравнения вышеприве-
–15,6 / cos a0 . Из третьего уравнения вышеприве-
дённой системы условий статики всей ВЧ1 находим
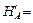
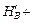 HD / cos a0 = 20,4 / cos a0 .
HD / cos a0 = 20,4 / cos a0 .
Для дальнейших расчётов удобно перейти к вертикальным и горизонтальным составляющим реакций ( по ( 2.17 ) – ( 2.19 )):
VA = 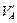 +
+ 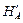 sin a0 = 68 + 20,4 tg a0 = 74,8 кН ;
sin a0 = 68 + 20,4 tg a0 = 74,8 кН ;
VB = 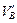 –
– 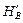 sin a0 = – 23 – (–15,6) tg a0 = –17,8 кН ;
sin a0 = – 23 – (–15,6) tg a0 = –17,8 кН ;
HA = 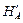 cos a0 = 20,4 кН ; HB =
cos a0 = 20,4 кН ; HB = 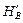 cos a0 = –15,6 кН.
cos a0 = –15,6 кН.
Проверку полученных значений реакций выполняем с помощью ранее не использованных уравнений равновесия:
– для левой половины ВЧ1 ( рис. 2.73, а ): 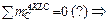 HA∙6 –
HA∙6 –
– VA∙3 + q∙6∙3 – M = 122,4 – 224,4 + 162 – 60 = 0;
– для вcей ВЧ1: S y = 0 (?)  VA +VB – VD – q∙6 = 74,8 –17,8 – 3 – 54 = 0.
VA +VB – VD – q∙6 = 74,8 –17,8 – 3 – 54 = 0.
Внутренние силовые факторы в сечениях стержней, образующих трёхшарнирный контур AKL в составе ВЧ1 , невозможно определить, пока этот контур не «раскрыт», т. е. не найдены силы взаимодействия между элементами в узлах A, K и L . Указанный фрагмент представляет собой трёхшарнирную систему с наклонной затяжкой, роль которой играет незагруженный прямолинейный элемент AK с шарнирами по концам, ра-
ботающий на осевое растяжение-сжатие. При
этом L можно рассматривать как ключевой
шарнир. Отделив сечением I – I по шарниру L
и стержню AK ( рис. 2.73, а ) нижнюю часть
( рис. 2.74 ), из условия равновесия 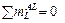
вычисляем продольную силу в стержне AK:
NAK = ( HA ∙ 5 – M ) / hN , где hN = 5 м ∙ sin b = 3 м;
NAK = 14 кН.
Далее находим HL = – 12 кН; VL = – 86 кН.
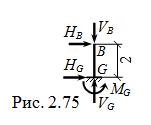
Реакции опоры главной части ( рис. 2.75 ) отыс-
киваются в последнюю очередь: HG = – HB ; VG = VB ;
MG = HB ∙ 2 м.
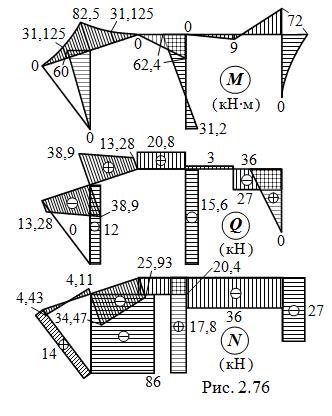
Используя известные из курса сопротивления материалов правила и приёмы определения внутренних силовых факторов в стержнях с прямолинейными и ломаными осями, строим эпюры изгибающих моментов, поперечных и продольных сил – они показаны на рис. 2.76, причём в пределах ВЧ2 эпюры – полученные ранее ( см. рис. 2.72 ).
Для примера рассмотрим наиболее сложный
участок KL ( рис. 2.77 ). Усилие NAK = 14 кН в стержне AK, приложенное на конце участка в точке K, для удобства раскладываем на вертикальную и горизонтальную составляющие 14 cos b =11,2 и 14 sin b = 8,4.
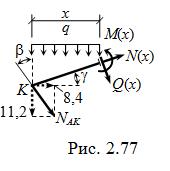
M(x) = – qx 2/2 – 11,2 x – 8,4 x tg g ;
Q(x) = – ( qx + 11,2 ) cos g – 8,4 sin g ;
N(x) = ( qx + 11,2 ) sin g – 8,4 cos g , где
g = arctg 1/3; sin g = 0,3162; cos g = 0,9487.
При x = 0 и x = 3 получаем значения усилий, указанные на рис. 2.76.
Контроль результатов расчёта осуществляем проверкой рав-новесия узлов и отсечённых частей рамы. Вырезав узел L, прикладываем к нему силовые факторы, «считанные» ( с учётом знаков ) с эпюр M, Q и N ( рис. 2.78, а,).
S mL = 82,5 – 82,5 + 60 – 60 = 0;
S x = 15 + (38,9 + 38,9 ) sin g –
– (4,11 + 34,47) cos g = – 0,0005  0;
0;
S y = 86 – (38,9 + 38,9 ) cos g –
– (4,11 + 34,47) sin g = – 0,008  0.
0.
Для узла D ( рис. 2.78, б,):
S mL = 62,4 – 62,4 = 0;
S x = 20,4 + 15,6 – 36 = 0;
S y = 20,8 – 17,8 – 3 = 0.
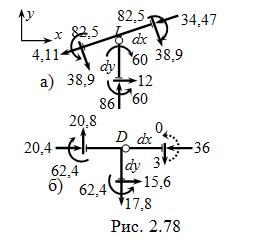
Аналогично проверяем равнове-
сие и других узлов, включая опорный A. Рис. 2.78
Рассматриваем также некоторую отсечённую часть рамы, например, показанную на рис. 2.79.
S mC= 11,2∙6 + 8,4∙2 + 36 – 60 + + 12∙3 – 86∙3 + q∙6∙3 + 62,4 –
– 17,8∙3 – 30∙6 + 27∙9 – 72 = 0;
S x = 8,4 + 12 + 15,6 – 36 = 0;
S y = – 11,2 + 86 – q∙6 – 17,8 –
– 30 + 27 = 0.
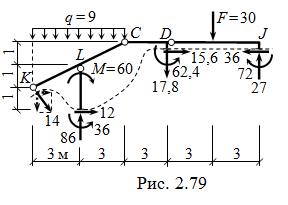
Для большей надёжности целесообразно выполнить проверку равновесия ещё одной-двух отсечённых частей и рамы в целом.
Определение перемещений от заданной нагрузки
Для отыскания угла поворота узла D рамы и вертикального перемещения точки K применяем метод Максвелла – Мора ( см. п. 1.5 и [1 – 4 ] ). Основным видом деформации всех элементов си-стемы, кроме AK, является изгиб, а стержень AK при заданной на-грузке испытывает чистое растяжение. Поэтому формулу Мак-свелла – Мора ( 1.27 ) используем в сокращённом виде ( без учёта податливости связей, так как все опоры жёсткие; а также сдвигов и продольных деформаций изгибаемых элементов ), принимая во внимание то, что в пределах j-го участка EI(xj) = const = EIj :
|

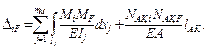
Переобозначив искомые перемещения jD 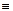 D1F и v K
D1F и v K 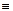 D2F , для их определения дополнительно рассматриваем два вспомогательных единичных ( фиктивных ) состояния рамы:
D2F , для их определения дополнительно рассматриваем два вспомогательных единичных ( фиктивных ) состояния рамы:
Ø с равным 1 моментом в узле D ( рис. 2.80, а );
Ø с единичной вертикальной силой в точке K ( рис. 2.80, б ).
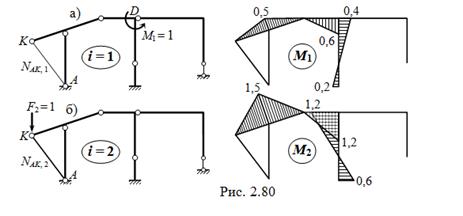
Для определения усилий в единичных состояниях рамы выполняем расчёты по той же схеме, что в случае действия заданной нагрузки ( см. выше ). При этом учитываем, что оба единичных воздействия приложены к части ВЧ1 ( см. с. 122 ), следовательно, самая второстепенная часть ВЧ2 не работает. В результате получаем эпюры изгибающих моментов M1 и M2 ( рис. 2.80, в, г ) и находим NAK, 1 = 1 / 6; NAK, 2 = –1 / 2.
Вычисление интегралов в формуле Максвелла – Мора – «пе-ремножение» единичной и «грузовой» эпюр – производим по фор-муле Симпсона ( см. с. 40 ) на участках KL, LC, DG и по правилу Верещагина ( см. с. 39 ) на участке CD ( число участков mM = 4 ):
|

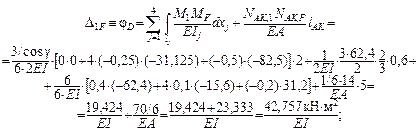
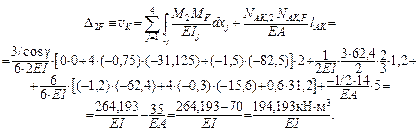 Знаки «+» у найденных jD и v K означают, что каждое из этих перемещений направлено в ту же сторону, что и соответствующее единичное воздействие, т. е. jD – против хода часовой стрел-ки, v K – вниз.
Знаки «+» у найденных jD и v K означают, что каждое из этих перемещений направлено в ту же сторону, что и соответствующее единичное воздействие, т. е. jD – против хода часовой стрел-ки, v K – вниз.
Ф а к у л ь т а т и в н о:

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

