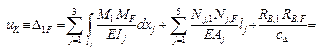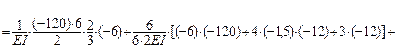Пример расчёта плоской комбинированной системы

    Требуется рассчитать комбинированную систему, изображённую на рис. 2.82, по указаниям, приведённым на с. 111. Принять EA = 1,5 м ^{– 2} EI.

 

Кинематический анализ

1. Проверка условия

W < 0, где W = 3D –

– (3П + 2H + C + C₀):

D = 8 (ADC, CK, KBG,

Dp, pr, rs, ps и sK);

П = 0; H = 10 ; C = 0 ; C₀ = 4;

W = 3∙8 – (0 + 2∙10 + 0 + 4) = 0.

 

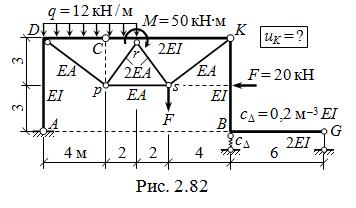
2. Структурный анализ: С K + rs + sK = D₁ ( соединение с помощью трёх шарниров); D₁ + Dp + ADC= D₂ (посредством трёх шарниров); «земля» + D₂ + KBG = ГНС (попарно с помощью двух шар-ниров A и K и пары опорных связей). Все связи наложены правильно. Напоминание: податливая опора B в структурном анализе считается жёсткой.  

Определение внутренних усилий и построение их эпюр

    В соответствии с подходом, изложенным на с. 109 – 110, выполняем расчёт системы в порядке, обратном последовательности шагов её образования, выявленной структурным анализом:

Ø в первую очередь находим реакции опор A, B, G и в шарнире K;

Ø разделив систему сечением по шарниру С и стержню Dp, определяем усилие N_Dp и реакции в шарнире C;

Ø последовательно вырезая узлы p и s, из условий их равновесия отыскиваем продольные силы в стержнях, испытывающих осевое растяжение или сжатие, – N_pr , N_ps , N_rs и N_sK ;

Ø найденные реакции связей и усилия в стержнях используем для вычисления внутренних силовых факторов в изгибаемых элементах.    

       Находим единственную горизонтальную опорную реакцию 

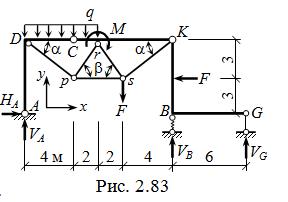
H_A ( рис. 2.83 ) : S x = 0 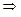H_A = F =  20 кН,

 после чего легко отыскивается V_A : 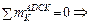V_A = ( H_A∙6 + q∙6∙9 – M + F∙4) / 12 = 66,5 кН.

    Далее определяем V_G : 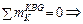  V_G = F∙3 / 6 = 10 кН и, на-конец, из условия S x = 0 для системы в целом: V_B = q∙6 + F – V_A – – V_G = 15,5 кН.

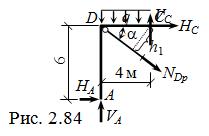
    Из равновесия части ADC ( рис. 2.84 ):

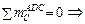N_Dp = ( V_A∙4 – H_A∙6 – q∙4∙2 ) / h₁ ,

где h₁ = 4 м∙sin a = 2,4 м; 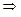N_Dp = 20,833 кН;

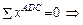        H_C = – 36,667 кН;

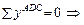        V_C = – 6 кН.

 

 

 

    Вырезав узел p ( рис. 2.85 ), имеем:

S y = 0 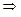N_pr = – N_Dp∙ sin a / sin b = – 15,024 кН;

                           ( sin a = 0,6;  sin b = 0,832 )

S x = 0 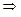N_ps = N_Dp∙cos a – N_pr ∙ cos b = 25 кН.

                     ( cos a = 0,8;  cos b = 0,5547 )

 

                     Аналогично для узла s ( рис. 2.86 ):

S y = 0 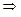  N_rs ∙ sin b + N_sK ∙ sin a  - F = 0;

S x = 0 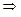N_sK ∙ cos a  - N_rs ∙ cos b - N_ps = 0,

откуда N_rs = 1,002 кН; N_sK = 31,944 кН.

 

        

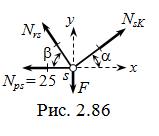
Используем найденные значения усилий в стержнях и реакций опор  для вычисления ( по схеме рис. 2.87, а ) изгибающих моментов, продольных и поперечных сил в элементах с преобладающим изгибом. Эпюры M, N и Q представлены на рис. 2.87, б – г.

 

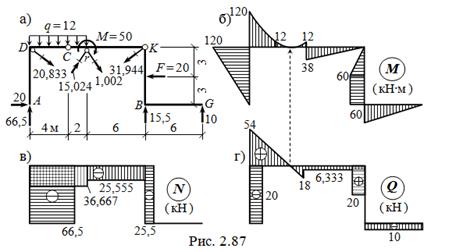
    Полученные результаты проверяются качественно – на соответствие построенных эпюр заданным нагрузкам ( см. с. 20 – 21 ) и количественно – контролем равновесия узлов, отсечённых частей и всей системы.

S m D = 120 – 120 = 0; S x = 20 + 20,833∙ cos a – 36,667 = – 0,0006 0; S y = 66,5 – 20,833∙ sin a – 54 = 0,0002 0.     Для узла r ( рис. 2.88, б ): S mr = 12 – 50 + 38 = 0; S x = 36,667 + (15,024 + 1,002) ∙ cos b – – 45,555  = 0,0016 0; S y = –18 + (15,024 + 1,002) ∙ sin b + 6,333 =   = – 0,0007 0.

    Рассматриваем узел D с приложенными к нему усилиями в концевых сечениях примыкающих элементов ( рис. 2.88, а ):

 

 

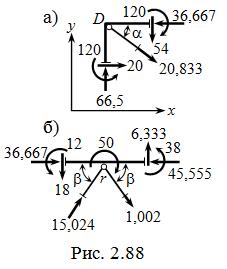
    Аналогично выполняется проверка вы-

полнения условий статики для узлов K и B.

    Далее контролируем равновесие отсе-

чённой части системы, для примера – показанной на рис. 2.89:

 

S m_r = 120 – 66,5 ∙ 6 + q ∙ 6 ∙ 3 +

+ 20,833 ∙ 6 ∙ sin a – 50 – 25 ∙ 3 –

– 20 ∙ 2 – 20 ∙ 3 + 60 + 25,5 ∙ 6 = 

= – 0,0012 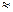0;

S x = 20 + 20,833 ∙ cos a +

+ 15,024 ∙ cos b – 25 – 20  =

= 0,0002 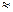0;

S y = 66,5 – 20,833 ∙ sin a – q ∙ 6 + +15,024 ∙ sin b – 20 +25,5 = 0,0002.

 

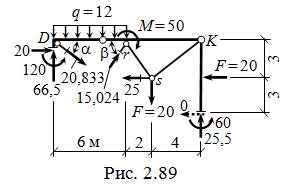
    Дополнительно можно осуществить статическую проверку для ещё одной – двух отсечённых частей и системы в целом.

Определение перемещения от заданной нагрузки

       Для отыскания горизонтального перемещения точки K используем метод Максвелла – Мора ( см. п. 1.5 и [1 – 4 ] ). В комбинированной системе объединены элементы, основным видом де-формации которых является изгиб, со стержнями, испытывающие чистое растяжение или сжатие. Кроме того, имеется упругоподатливая  опора  В.  Поэтому  формулу  Максвелла – Мора

( 1.27 ) применяем в виде         

482.3

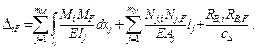
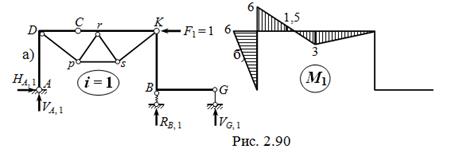
    Переобозначив искомое перемещение u_K 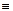D_1F , для его определения дополнительно рассматриваем вспомогательное единичное ( фиктивное ) состояние системы с горизонтальной силой в узле K, равной 1 ( рис. 2.90, а ). Выполняя расчёт по той же схеме, что в действительном состоянии ( см. с. 129 – 130 ), находим

 

 

H_{A, 1} = 1;  V_{A, 1} = – R_{B, 1} = 1 / 2;  V_{G, 1} = 0;  N_{Dp, 1} = N_{sK, 1} = – 5 / 3;  N_{ps, 1} = – 2;   N_{pr, 1} = N_{rs, 1} = 1,2019.

      

Далее определяем изгибающие моменты от F₁ = 1 – эпюра   приведена на рис. 2.90, б.

    «Перемножение» единичной M₁ и «грузовой» эпюр моментов для вычисления интегралов в формуле Максвелла – Мора производим по формуле Симпсона ( см. с. 40 ) на участке Dr ( шарнир С не является границей участков ) и по правилу Верещагина   ( см. с. 39 ) на участках AD и rK ( имеем m_M = 3 ). Число элементов с учитываемыми продольными деформациями ( на исходной рас-чётной схеме обозначены типом жёсткости EA ) m_N = 5.

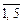    Используя эпюру M с рис. 2.87, б  в качестве M_F , а также ра-нее найденные значения V_B , N_Dp , N_pr , …, N_sK ( см. с. 130 ) соответственно как R_{B, F} и N_{j , F}  ( j = ), вычисляем

 

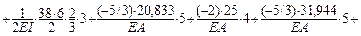
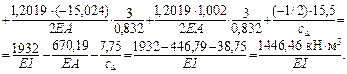
    Знак «+» результата означает, что направление перемещения u_K – такое же, как у силы F₁ = 1, т. е. влево.

 

Ф а к у л ь т а т и в н о: