Расчёт трёхшарнирной арки, статически определимой плоской рамы и комбинированной системы

1₂_.3

2.4.1. Общие сведения

Трёхшарнирной называется плоская геометрически неизменяемая система, состоящая из трёх дисков, попарно соединённых тремя шарнирами.

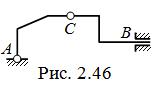
Как правило, шарниры в трёхшарнирной системе ( ТШС ) – цилиндрические ( в дальнейшем рассматриваются исключительно такие системы ), но могут присутствовать и поступательные шарниры ( рис. 2.46 ) .

Три цилиндрических шарнира не должны располагаться на одной прямой

4₂_.3

Различают два основных типа

трёхшарнирных систем:

* распорные ( внешне распорные ), в которых один из трёх дисков – «земля» ( рис. 2.47, а ); в таких системах шарниры A и B, соединяющие два диска с «землёй», называются опорными ( A и B могут быть верхними шарнирами неподвижных шарнирных опор – рис. 2.47, б ), а шарнир С между этими дисками – ключевым; горизонтальная составляющая опорной реакции при вертикальной нагрузке именуется распором;

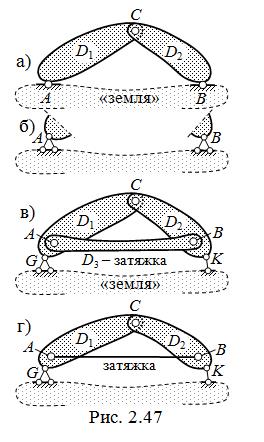
* трёхшарнирные системы с затяжкой ( внутренне распорные ) – рис. 2.47, в; обычно затяжка – прямолинейный стержень, работающий на

растяжение ( рис. 2.47, г ); соединённые в один диск три диска D₁ , D₂ и D₃ ( затяжка ) прикрепляются к «земле» тремя связями, как правило, в виде шарнирных опор – одной неподвижной и одной по

3₂_.3

движной ( рис. 2.47, в, г ).

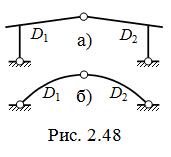
В зависимости от того, чтó представляют собой диски D₁ и D₂ , принято выделять трёхшарнирные рамы (с прямолинейными участками – рис. 2.48, а ) и арки ( диски D₁и D₂ – криволинейные стержни – рис. 2.48, б ); трёхшарнирной системой может быть также ферма ( рис. 2.25, б ).

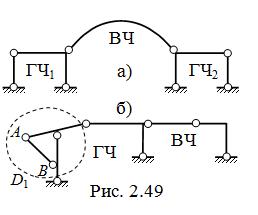
Трёхшарнирные арки и рамы могут присутствовать в составных системах в качестве главных и второстепенных частей ( рис. 2.49 ), также образовывать некоторые составные диски ( D1 на рис. 2.49, б, где стержень AB играет роль наклонной затяжки ).

6₂_.3

Определение реакций связей в трёхшарнирных системах

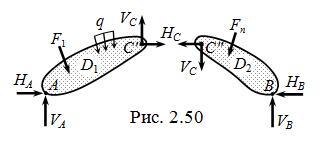
Для внешне распорной ТШС ( рис. 2.47, а, б ) применение принципа освобождения от связей – четырёх внешних в опорах А и B и двух внутренних в ключевом шарнире C – приводит к выявлению шести составляющих реакций связей: H_A , V_A , H_B , V_B , H_C , V_C ( рис. 2.50 ).

Для двух плоских дисков можно записать суммарно шесть уравнений равновесия – достаточно для отыскания всех реакций.

Максимально просто реакции связей вычисляются по следующему алгоритму ( нагрузка – общего вида в плоскости; взаимное расположение опор – произвольное, т. е. на разных уровнях ):

1) опорные реакции R_A и R_B раскладываются на составля-ющие – вертикальные 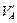, 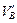и наклонные 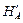, 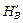вдоль линии, соединяющей опорные шарниры ( рис. 2.51, а );

2) записываются уравнения равновесия всей системы:

S m_A = 0; S m_B = 0; S x = 0; ( 2.13 )

из первого сразу находится вертикальная реакция правой опоры

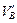= S m_A_,_F / l ; из второго – аналогично 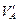= S m_B_,_F / l , ( 2.14 )

где S m_A_,_F и S m_B_,_F – соответственно суммы моментов всех нагру-

зок относительно точек A и B. Третье уравнение ( 2.13 ) даёт

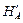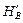= – S F_x / cos a₀ ( 2.15 )

( здесь S F_x – сумма проекций нагрузок на ось x );

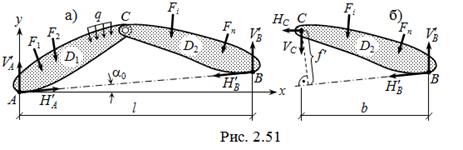
3) производится разделение системы на два диска сечением по ключевому шарниру С ( эта операция является обязательной в расчёте трёхшарнирной системы ) и рассматривается равновесие правого или левого диска ( удобнее – с меньшим числом нагрузок ) – рис. 2.51, б:

– из уравнения 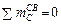моментов относительно точки С нахо-дится реакция опоры 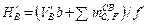, ( 2.16 )

где 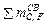– сумма моментов нагрузок, приложенных к части СВ,

относительно точки С ( положительные моменты – против хода

часовой стрелки );

– два других уравнения S x ^CB = 0 и S y ^CB = 0 позволяют определить H_C и V_C ;

4) по зависимости ( 2.15 ) вычисляется последняя реакция .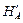

Уравнения равновесия другой ( здесь – левой ) части ТШС могут быть использованы для проверки правильности найденных реакций связей.

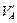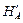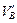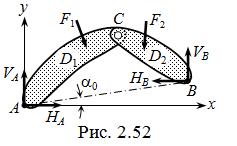
От вычисленных , , , 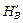можно перейти к ортого-

гональным составляющим опорных реакций ( рис. 2.52 ), более

удобным для последующих расчётов

внутренних усилий :

V_A = 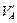+ 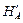sin a₀ ; ( 2.17 )

V_B = 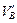– 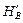sin a₀ ; ( 2.18 )

H_A = 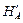cos a₀ ; H_B = 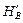cos a₀ ( 2.19 )

( на схеме a₀> 0 ).

Ч а с т н ы е с л у ч а и

1. Все нагрузки – вертикальные ( S F_x = 0 ): из ( 2.15 ) следует 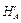= 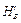( = H – распор ).

9₂_.3

2. Опоры A и B – на одном уровне ( a₀ = 0 ): в ( 2.14 ) – ( 2.16 ) вместо

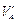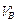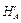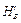вводятся V_A , V_B , H_A , H_B ; f ' заменяется на f.

Особый случай:

два из трёх шарниров располагаются на одной вертикали ( рис. 2.53, а ) или горизонтали ( рис. 2.53, б ):

целесообразно отступить от вышеизложенного алгоритма и, используя ортогональные составляющие опорных реакций, начинать их определение с уравнения равновесия той части, которой принадлежат упомянутые пары шарниров. Для трёхшарнирной рамы, изображённой на рис. 2.53, а: 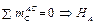; для системы

10₂_.3

на рис. 2.53, б:

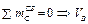. Остальные три реакции находятся из условий равновесия системы целом – для левой рамы

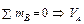, для правой –

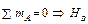, далее S x = 0 и S y = 0.

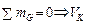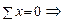
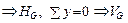Для ТШС с затяжкой ( рис. 2.47, в, г ) в первую очередь определяются реакции трёх внешних связей (

), затем из уравнений равновесия затяжки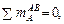

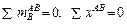отыскиваются

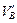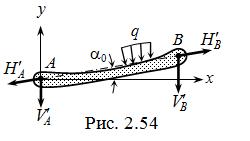
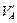, ( рис. 2.54 ) и зависимость между 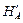и 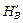. Реакция 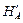или 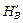находится тем же приёмом, что и в расчёте внешне распорной ТШС ( см. выше ) – из рассмотрения одного из дисков D₁или D₂ ; при этом вместе с нагрузками учитываются уже найденные реакции опор G или K.

12₂_.3

2) если нагрузка на затяжке отсутствует, то

Частные случаи: 1) при вертикальной нагрузке на затяжке

13₂_.3

Внутренние силовые факторы в трёхшарнирных системах

В поперечном сечении стержневого диска трёхшарнирной системы при заданных нагрузках возникают изгибающий момент, поперечная и продольная силы ( рис. 2.55 ).

При произвольной нагрузке усилия M, N и Q отыскиваются по правилам сопротивления материалов – из условий равновесия отсечённой части.

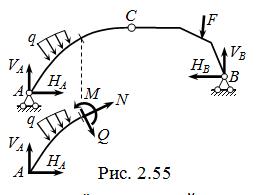
В случае действия только вертикальных нагрузок для вычисления «вручную» силовых факторов в произвольном сечении трёхшарнирной арки или рамы с опорами на одном уровне ( рис. 2.56, а ) удобно использовать

специальные формулы, выражающие искомые усилия в ТШС через изгибающие моменты и поперечные силы в шарнирно опёртой по концам балке того же пролёта и при действии такой же нагрузки, что и рассчитываемая ТШС ( рис. 2.56, б ), а также через распор H арки (рамы) и геометрические параметры сечения ТШС – координаты x и y(x) его центра тяжести и угол наклона q (x) сечения к вертикали ( или такой же угол между касательной к оси стержня и горизонтальной осью x ):

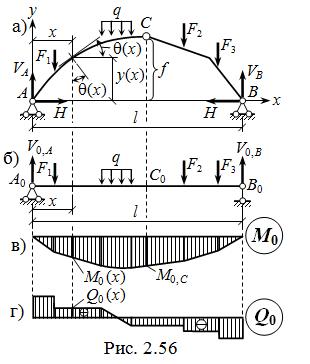
M (x) = M₀ (x) – H ∙ y (x); ( 2.20 )

Q (x) = Q₀ (x) ∙ cos q (x) – H ∙ sin q (x); ( 2.21 )

N (x) = – [ Q₀ (x) ∙ sin q (x) + H ∙ cos q (x) ], ( 2.22 )

где M (x), Q (x), N (x) – усилия в сечении арки (рамы) с абсциссой x;

M₀ (x) и Q₀ (x) – балочные изгибающий момент и поперечная

14₂_.3

сила в сечении с координатой x (рис. 2.56, в, г).

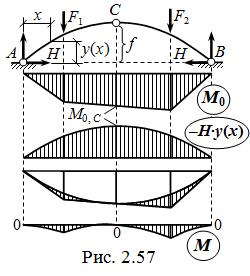
Зависимость ( 2.20 ) не только облегчает вычисление изгибающего момента в любом сечении ТШС, но и позволяет предсказывать вид всей эпюры M ( пример – на рис. 2.57, где, как и везде далее, эпюра построена не на оси арки, а на её горизонтальной проекции ). Заметим, что, во-первых, из условия MC = 0 распор определяется как

H = M₀, C / f , ( 2.23 )

а во-вторых, из-за криволинейности оси арки изгибающие моменты в ней изменяются по длине нелинейно даже при отсутствии распределённых

18₂_.3

нагрузок. Нелинейными, согласно ( 2.21 ) и ( 2.22 ), должны быть также и эпюры Q и N в арке. При построении и проверке эпюр внутренних силовых факторов на криволинейных участках трёх-шарнирных систем ( в частности, в арках ), полезно учитывать дифференциальные уравнения равновесия ( рис. 2.58 )

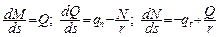, ( 2.24 )

из которых первое аналогично ( 1.13 ) для

20₂_.3

прямолинейного стержня, а из двух других

достаточно просто использовать последнее: на участке без распределённой нагрузки ( q_t = 0 ), в точке, где Q = 0, N – экстремальная.

Заметим, что из ( 2.24 ) при r = 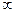получаются уравнения ( 1.12 ) – ( 1.14 ) для прямого стержня, практическое примене

21₂_.3

ние которых описано в форме рекоменда

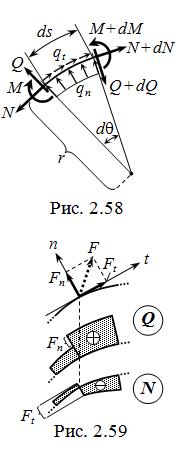
ций и правил на с. 19 – 21. Изложенные там указания относительно особенностей эпюр (изломов и скачков ) в точках приложения сосредоточенных сил и моментов имеют силу как для прямых, так и для криволинейных стержней – на эпюре Q от силы F, наклонной к оси стержня ( рис. 2.59 ) – скачок на проекцию F_n , на эпюре N – на F_t .

Описания характера эпюр ( прямые, кривые ), приведённые в табл. 1.1, относятся только к прямым стержням, для арок они недействительны.

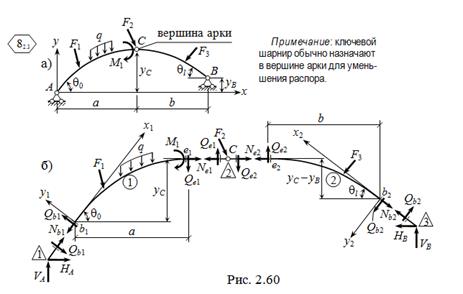
Определение усилий в трёхшарнирных системах на базе об-щего конечно-элементного подхода осуществляется по алгорит-му, изложенному в п. 1.3.1; для рам – как в примере, приведённом на с. 13 – 18; для арки ( рис. 2.60, а ) – по расчётной схеме, показанной на рис. 2.60, б, где заведомо равные нулю моменты в концевых сечениях двух элементов-полуарок у шарнирных узлов не обозначены, и в вектор искомых силовых факторов они не включаются:

S = [ Q_b₁ N_b₁ Q_e₁ N_e₁ Q_b₂ N_b₂ Q_e₂ N_e₂ V_A H_A V_B H_B ]^т ( n_S = 12 ).

Полная система уравнений A∙S + B_F = 0 формируется из условий равновесия двух элементов

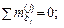
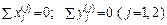( 2.25 )

и трёх узлов: 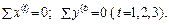( 2.26 )

Уравнения третьей группы ( см. с. 18 ) не записываются, так как равенство нулю моментов в концевых сечениях у шарниров уже учтено при составлении вектора S. Раскрывая ( 2.25 ) и ( 2.26 ),

получаем матрицу коэффициентов

m x y m x y x y x y x y

A =

Q_b₁ N_b₁ Q_e₁ N_e₁ Q_b₂ N_b₂ Q_e₂ N_e₂ V_A H_A V_B H_B

		– a	– y_C
	– 1	-sin q₀	cos q₀
1		-cos q₀	-sin q₀
						– b	y_C – y_B
					– 1	sin q_l	cos q_l
				1		-cos q_l	sin q_l
sin q₀	cos q₀								1
-sin q₀	sin q₀							1
			– 1				1
		1				– 1
				sin q_l	-cos q_l						–1
				cos q_l	sin q_l					1

и вектор свободных членов уравнений ( от нагрузки ):

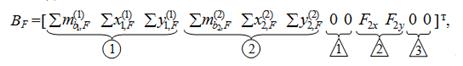
где 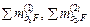– суммы моментов нагрузок, приложенных к

1-му и 2-му элементам-полуаркам, относительно точек b₁ и b₂ ;

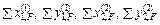– суммы проекций внеузловых на-

грузок на собственные оси x₁, y₁, x₂, y₂элементов 1 и 2;

F₂_x , F₂_y – проекции нагрузки в узле 2 на глобальные оси x и y.

Предыдущая 1 234 5 6 7 8 9 10 Следующая