 |
Главная |
Определение продольных сил загружением линий влияния. Расчётные усилия
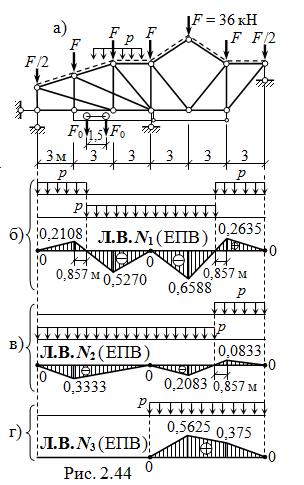
Используем построенные линии влияния для определения усилий в стержнях фермы от постоянной нагрузки в виде сосредоточенных сил по верхнему поясу фермы ( рис. 2.44, а ), а также максимальных и минимальных значений продольных сил от вре-менных нагрузок – снеговой по верхнему поясу ( учитывается как распределённая по длине горизонтальной проекции фермы, интенсивностью p = p0 ∙ B0 = 1,5 кН / м2 ∙ 6 м = 9 кН / м ), и крановой в виде двух одинаковых сил давления колес крана по F0 = Fк / 2 = 10 кН ( по вспомогательным элементам, прикреплённым в узлах нижнего пояса ).
Усилия N1, N2 и N3 от постоянной нагрузки
Используем линии влияния в варианте «езда поверху» и вычисляем продольные силы по формуле N = S F ∙ yF: а)
N1, const = 36 кН ∙ (0,2108 – 0,5270 – 0,6588 + 0,2635) = – 25,61 кН;
N2, const = 36 кН ∙ (– 0,3333 – 0,1667 – 0,2083 + 0,0833) =
= – 22,50 кН;
N3, const = 36 кН ∙ ( 0,5625 + 0,375) = 33,75 кН – полное совпадение со значениями усилий, вычисленными ранее «вручную» и по программе FERSO.
Усилия от временных нагрузок
Невыгоднейшие положения снеговой нагрузки, которым отвечают максимальные и минимальные значения продольных сил в стержнях, показаны на рис. 2.44, б – г.
Максимальные и минимальные усилия от крановой нагруз-ки находим с помощью линий влияния при загружении нижнего пояса с учётом узловой передачи нагрузки ( рис. 2.45 ):

Экстремальные усилия от снеговой нагрузки определяем как
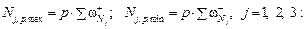
– по рис. 2.44, б:
N1, p, max = 9 кН / м ∙ (0,2108 ∙ 3,857 м / 2 + 0,2635 ∙ 3,857 м / 2) = 8,23 кН;
N1, p, min = – 9 кН / м ∙ (0,527 ∙ 5,143 м / 2 + 0,6588 ∙ 5,143 м / 2) = –27,44 кН;
– по рис. 2.44, в:
N2, p, max = 9 кН / м ∙ 0,0833 ∙ 3,857 м / 2 = 1,45 кН;
N2, p, min = – 9 кН / м ∙ (0,3333 ∙ 9 м / 2 + 0,2083 ∙ 5,143 м / 2) = –18,32 кН;
– по рис. 2.44, г:
N3, p, max = 9 кН / м ∙ (0,5625 + 0,375) ∙ 3 м = 25,31 кН;
N3, p, min = 0 ( при отсутствии снега на покрытии ).
N1, к, max = 10 кН∙ (0,1976 + 0,2635) = 4,61 кН;
N1, к, min = 0 ( при демонтирован-
ном кране );
N2, к, max = 10 кН∙ (0,125 + 0,1667) =
= 2,92 кН;
N2, к, min = – 10 кН∙ (0,3333 + 0,25) =
= – 5,83 кН;
N3, к, max = 10 кН∙ (0,2812 + 0,375 ) =
= 6,56 кН;
N3, к, min = 0.
Расчётные значения про-
дольных сил
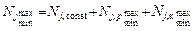
вычисляем в табличной форме:
| j (№ стер-жня) |
Nj,const | Усилия от временных нагрузок | Расчётные усилия | ||||
| Nj, p, max | Nj, p, min | Nj, к, max | Nj, к, min | Nj max | Nj min | ||
| 1 | –25,61 | 8,23 | –27,44 | 4,61 | 0 | –12,77 | –53,05 |
| 2 | –22,50 | 1,45 | –18,32 | 2,92 | –5,83 | –18,13 | –46,65 |
| 3 | 33,75 | 25,31 | 0 | 6,56 | 0 | 65,62 | 33,75 |
2. 3 .5 . Контрольные вопросы по теме 2. 3
1. Что такое ферма? (71)
2. Что называется поясами, решёткой фермы? (71)
3. Классификация ферм по типу решётки. (71)
4. Какие решётки ферм относятся к простым, а какие к сложным? (перечислить). (71)
5. Необходимое условие геометрической неизменяемости фермы; формула для W. (72)
6. Структурный анализ ферм. Основной приём синтеза ферм. (72)
7. Особенности загружения и характер работы стержней фермы. (71)
8. Какие внутренние силовые факторы возникают в поперечных сечениях стержней фермы? (71)
9. Растянуты или сжаты стержни верхнего пояса простой однопролётной фермы при вертикальной нагрузке между опорами, направленной вниз? А стержни нижнего пояса? [1 – 4]
10. Классификация методов и способов определения усилий в стержнях ферм. (72)
11. Частные случаи равновесия узлов фермы. (73)
12. Как можно обнаружить неработающие стержни фермы при заданной нагрузке? (объяснить на примере).
13. Способ моментной точки (способ Риттера) – основной случай (идея способа); особые случаи. (73)
14. Способ проекций; условие его рационального применения. (73)
15. Способ совместных сечений. (74)
16. Какие способы рациональны для определения усилий в стержнях а) пояса фермы с простой решёткой? б) простой решётки фермы с параллельными поясами? (Самостоятельно)
17. Особенности конечно-элементного алгоритма формирования пол-ной системы уравнений статики для фермы. (75)
18. Особенности линий влияния усилий в стержнях ферм. (75)
19. Учёт узловой передачи нагрузки при построении линий влияния усилий в стержнях ферм. (31, 91)
20. Как получаются соединительные прямые на линии влияния усилия в стержне фермы при езде поверху и понизу? (77)
21. Правила построения линии влияния усилия в стержне фермы, определяемого способом
а) вырезания узла; (75) б) моментной точки; (77) в) проекций. (77)
22. Изобразить типовые линии влияния усилий в балочных фермах (76):
– в поясе;
– в раскосе фермы с простой решёткой.
– в раскосе фермы с параллельными поясами и треугольной решёткой;
– в стойке трапецеидальной балочной фермы;
– в стойке треугольной фермы с раскосной решёткой;
– в одиночном стержне трёхстержневого узла частного вида.
23. Основная расчётная формула кинематического метода для построения линий влияния усилий в стержнях ферм. (79)
24. Что такое dN при построении линии влияния усилия в стержне фермы кинематическим методом? (24)

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

