Динамика розничного товарооборота области

(включая общественное питание)

Годы	Розничный товарооборот, млн. руб.	Темп роста, %
по сравнению с предшествующим периодом – цепные	по сравнению с 2000 – базисные
	270,5	-
	286,0	105,7	105,7
	295,7	103,4	109,3
	305,8	103,4	113,0
	316,0	103,4	116,8
200х	324,2	102,6	119,9

 

Данные таблицы подтверждают, что розничный товаро­оборот за 2000 – 200х гг. непрерывно возрастал.

Пример 7. Имеются следующие данные о числе предприятий розничной торговли государственных орга­низаций и ЧП по типам предприятий по состоянию на конец 2004 г. (тыс.):

Типы предприятий	Число розничных торговых предприятий
государственная торговля	торговля ЧП
Магазины	237,8	315,4
Палатки	97,5	65,6
Итого	335,3	381,0

Исчислите относительные показатели структуры типов розничных торговых предприятий государственной и коопе­ративной торговли на конец 2004 г.

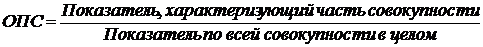
Решение. Для расчета относительных показателей структуры сопоставим численности торговых предприятий по типам (f_i) с общим итогом (åf), т. е. определим удельный вес в процентах ( ).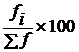

Магазины:

в государственной торговле в торговле ЧП

; .

 

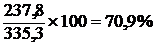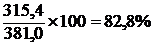Палатки:

в государственной торговле в торговле ЧП

; .

 

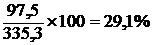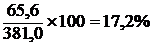Исчисленные относительные показатели структуры следует представить в таблице.

Таблица 9

Структура розничных торговых предприятий государственной торговли

и торговли ЧП по состоянию на 1 января 2005 г. (%)

Типы предприятий	Число розничных торговых предприятий
государственная торговля	торговля ЧП
Магазины	70,9	82,8
Палатки	29,1	17,2
Итого

 

Данные таблицы показывают, что в кооперативной тор­говле удельный вес магазинов выше, чем в государственной торговле, и значительно ниже удельный вес палаток.

 

Пример 8. На начало мая 2005 г. численность граждан, состоящих на учете в службе занятости, составляла 3064 человека, а число заявленных предприятиями вакансий – 309.

 

= .

 

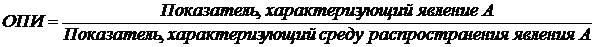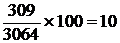Этот показатель свидетельствует о том, что на каждых 100 незанятых приходилось 10 свободных мест.

Пример 9. Имеются данные о среднегодовой численности рабочих и служащих района за 2005 г. (тыс. чел.):

 

Всего рабочих и служащих 10,9

в том числе:

рабочих, включая младший обслуживающий

пер­сонал и работников охраны 7,6

служащих 3,3

 

Исчислите, сколько служащих приходится на 100 ра­бочих.

 

 

Решение. Относительная величина координации будет определена так: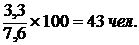

Следовательно, на каждые 100 рабочих (включая млад­ший обслуживающий персонал и работников охраны) по району 2005 г. приходилось 43 служащих.

 

 

Тема 3. СРЕДНИЕ ВЕЛИЧИНЫ

ЗАДАЧИ

№ 1. Пять бригад рабочих обрабатывают один и тот же вид деталей. Дневная выработка деталей на день обследо­вания отдельными рабочими характеризуется следующими данными:

Порядковый номер рабочего	Дневная выработка рабочего, шт.
1-я бригада	2-я бригада	3-я бригада	4-я бригада	5-я бригада
	—			—	—
	—		—	—	—

 

Определите среднее дневное число деталей, обрабо­танных одним рабочим: 1) для каждой бригады, дайте сравнительную характеристику этих средних; 2) для всех бригад в целом, используя: а) непосредственно данные ус­ловия задачи, б) вычисленные показатели средней дневной выработки по пяти бригадам.

Ответьте на вопрос, как изменится среднедневная вы­работка рабочего по каждой бригаде, если все индивидуаль­ные значения выработки: а) увеличить на 5 единиц; б) умень­шить на 5 единиц; в) увеличить в два раза; г) уменьшить в два раза.

№ 2. Имеются следующие данные о тарифном разряде трех групп рабочих:

Порядковый номер рабочего	Тарифный разряд
1-я бригада	2-я бригада	3-я бригада

 

Определите средний тарифный разряд рабочих каж­дой бригады: а) методом простой (невзвешенной) средней; б) методом взвешенной средней.

№ 3. Месячная выработка продавцов по трем отделам магазина бытовой техники характеризуется следующими дан­ными:

I отдел	II отдел	III отдел
выработка, тыс. руб.	число про­давцов, чел.	выработка, тыс. руб.	число про­давцов, чел.	выработка, тыс. руб.	число про­давцов, чел.

 

Определите среднюю выработку продавцов по каж­дому отделу и по магазину в целом. Укажите, какие виды средней нужно применять.

№ 4. Распределение студентов по успеваемости (резуль­тат экзамена) характеризуется следующими данными:

Номер академической группы	Экзаменационный балл	Число студентов
	-

Определите средний балл экзаменационной оценки 1) для каждой академической группы студентов, дайте сравнительную характеристику; 2) для всех академических групп в целом, используя: а) непосредственно данные условия задачи, б) вычисленные показатели среднего экзамена­ционного балла по пяти академическим группам.

 

№ 5. Распределение пред­приятий по размеру прибыли характеризуется следующими данными:

Группы предприятий по размеру прибыли, тыс. руб.	Количество предприятий
I регион	II регион	III регион
До 300
300 – 500
500 – 700
Свыше 700
Итого

Определите средний размер прибыли, приходящейся на одно предприятие: а) по каждому региону; б) по трем регионам вместе, используя полученные показатели средне­го размера прибыли по регионам.

№ 6. Имеются следующие данные о сроке службы стан­ков по пяти основным цехам промышленного объединения:

Срок службы станков, лет	Количество станков, шт.
цех № 1	цех № 2	цех № 3	цех № 4	цех № 5
До 5
5 – 10
10 – 15
15 и более

Определите средний срок службы станков по каждому цеху, используя в качестве весов: а) абсолютные показатели (количество станков); б) относительные показатели структуры распределения станков (проценты, коэффициен­ты).

 

№ 7. Имеются следующие данные о производстве и себе­стоимости продукции «А» по двум предприятиям:

Предприя-тие, №	I квартал	II квартал
себестои­мость еди­ницы, тыс. руб.	производст­во, тыс. шт.	себестои­мость еди­ницы, тыс. руб.	производст­во, тыс. шт.
	7,0		6,5
	11,0		10,8

Определите среднюю себестоимость продукции за кварталы.

Объясните, почему при более низкой себестоимости по каждому предприятию во втором квартале средняя себестои­мость оказалась выше, чем в первом квартале.

№ 8. Имеются следующие данные о заработной плате ра­бочих по двум цехам завода:

Цех, №	Сентябрь	Октябрь
средняя заработная плата, у.е.	число рабочих, чел.	средняя заработная плата, у.е.	число рабочих, чел.

Определите среднюю заработную плату рабочих по двум- цехам: а) за сентябрь; б) за октябрь; в) за два меся­ца. Какие виды средней используются в каждом случае? По­ясните полученные результаты.

 

№ 9. Имеются следующие данные о работе промышлен­ных предприятий объединения:

Предприятие, №	План вы­пуска про­дукции, тыс. руб.	Фактиче­ский вы­пуск про­дукции, тыс. руб.	Выполнение плана, %	Продукция высшего сорта, %
А
I			100,0	65,1
II			100,7	64,2
III			98,8	58,5
IV			103,3	70,3

Определите: 1) средний процент выполнения плана предприятиями отрасли, используя показатели: а) гр. 1 и 2, б) гр. 1 и 3, в) гр. 2 и 3; 2) средний процент продукции высшего сорта.

 

№ 10. В результате статистического обследования пяти районов области получены следующие данные по распреде­лению семей по числу детей:

Число детей	Количество семей, в % к итогу
1-й район	2-й район	3-й район	4-й район	5-й район
6 и более
Итого

Определите моду и медиану по каждому ряду расп­ределения.

№ 11. Распределение рабочих предприятия по степени выполнения норм выработки за I квартал характеризуется следующими показателями:

Группы рабочих по выполнению норм выработки, %	Число рабочих, в % к итогу
январь	февраль	март
До 90			—
90 – 100
100 – 110
110 – 120
120 – 130
130 – 140
140 – 150
Итого

Определите моду и медиану по каждому ряду распре­деления.

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

Пример 1. Заработная плата бригады строителей по отдельным профессиям за месяц характеризуется следующими данными:

Маляры	Штукатуры	Кровельщики
заработная плата, у.е.	число рабо­чих, чел.	заработная плата, у.е.	число рабо­чих, чел.	заработная плата, у.е.	число рабо­чих, чел.
Итого		-		-

 

Определите среднюю заработную плату рабочих по -каждой профессии и в целом по бригаде.

Решение. Число рабочих известно. Исчислим фонд зара­ботной платы маляров путем суммирования заработка каждо­го рабочего. В данном случае веса (частоты) равны едини­це Следовательно, расчет средней заработной платы рабочих производится по формуле средней арифметической простои:

 

 

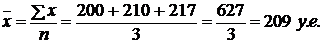
Если веса (частоты) в рядах распределения равны между собой, как это имеет место в бригаде штукатуров, расчет средней производится по формуле средней арифметической простой. Следовательно, средняя заработная плата штукату­ров будет равна:

 

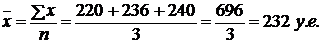
Если частоты имеют различные количественные значения, как в группе кровельщиков, то средняя заработная плата определяется по формуле средней арифметической взвешенной:

 

 

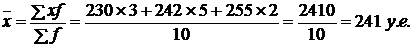
В этом примере фонд заработной платы равен сумме произведений заработной платы каждого рабочего на их число.

Средняя заработная плата рабочих бригады строителей может быть определена двумя способами:

а) отношением фонда заработной платы рабочих по груп­пам профессий к общей численности рабочих этих групп:

 

 

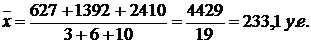
б) как средняя арифметическая взвешенная из группо­вых средних:

 

 

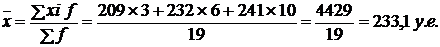
Пример 2. По данным обследования получены следующие данные о распределении студентов-заочников по возрасту:

Группа, № п/п	Группы студентов по возрасту, лет, x	Число студентов, чел., f	Удельный вес студентов в группе
в %, f¢	в коэффициентах, f¢¢
А	Б
I	20 – 25			0,10
II	25 – 30			0,45
III	30 – 35			0,40
IV	35 - 40			0,05
	Итого			1,00

Определите средний возраст студентов-заочников.

Решение. Среднее значение признака по данным вариа­ционного ряда распределения определяется по средней арифметической взвешенной:

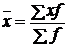
Чтобы применить эту формулу, надо значения признака в интервале (варианты) выразить одним числом, т. е. диск­ретной величиной, за которую принимается середина интер­вала каждой группы. Так, варианта первой группы 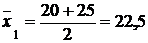и т. д. по остальным группам. Расчеты удобнее располагать в таблице:

Группы студентов по возрасту, лет, x	Число студентов, чел., f	Средина интервала, x	xf	xf¢	xf¢¢
20 – 25		22,5			2,25
25 – 30		27,5		1237,5	12,375
30 – 35		32,5			13,00
35 - 40		37,5		187,5	1,875
Итого		-		2950,0	29,5

 

Таким образом,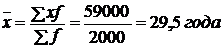

Аналогично производятся расчеты, если в качестве весов (частот) взяты относительные величины, которые могут быть выражены в процентах или коэффициентах (гр. 2,3 условия задачи). Следовательно, средний возраст студентов- заочни­ков, исчисленный по относительным величинам, будет равен:

а) если весами являются проценты -

 

 

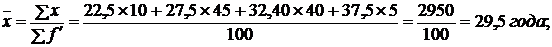
б) если весами являются коэффициента –

 

 

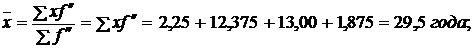
Получен тот же результат.

В рядах распределения с открытыми интервалами вели­чина интервала условно принимается равной интервалу со­седних групп. Если, например, первая группа студентов име­ет возраст до 25 лет, а четвертая – свыше 35 лет, то интер­вал первой группы приравнивается к интервалу следующей за ней второй группы, а четвертой – величине интервала предшествующей третьей группы. Дальнейший расчет ана­логичен изложенному выше.

Пример 3. Распределение промышленных предприятий отрасли по численности работающих характеризуется следующими данными:

 

Группы предприятий по числу работающих, чел.	Число предприятий
До 5000
5000 – 6000
6000 – 7000
7000 – 8000
Свыше 8000
Итого

 

Определить среднюю- численность работающих на предприятиях отрасли, применяя способ моментов.

Решение. Способ моментов основан на применении мате­матических свойств средней арифметической взвешенной и позволяет значительно упростить технику вычисления. Рас­чет производится по формуле:

 

 

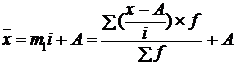
где А – постоянная величина, на которую уменьшаются все значения признака. В вариационных рядах с равными интервалами в качестве такой величины принимается варианта ряда с наиболь­шей частотой;

i – величина интервала ряда.

 

Метод расчета представим в следующей таблице:

Группы предприятий по числу работающих, чел., x	Число предприятий, f	Середина интервала, x	х – А = = х – 6500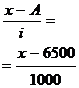
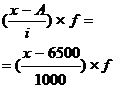
До 5000			- 2000	- 2	- 40
5000 – 6000			- 1000	- 1	- 40
6000 – 7000
7000 – 8000
Свыше 8000
Итого					- 10

 

По данным примера А = 6500, i = 1000.

Подставив данные таблицы в формулы, получим:

,

 

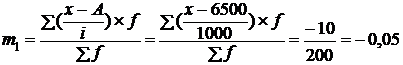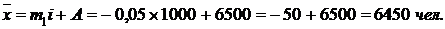
Средняя численность работающих на предприятии отрас­ли составляет 6450 чел.

Пример 4. Средняя выработка продукции на одного рабочего за смену в двух цехах завода, вырабатывающих однородную продукцию, характеризуется следующими данными:

Брига­да, №	Цех № 1	Бригада, №	Цех № 2
дневная выработ­ка продук­ции, шт., х	число рабо­чих, чел., f	дневная выработ­ка продук­ции, шт., х	объем произведенной продукции, шт., М
I			IV
II			V
III			VI

Определим среднедневную выработку продукции рабочих: а) по первому цеху; б) по второму цеху.

Решение. Основой расчета является экономическое содер­жание показателя:

 

 

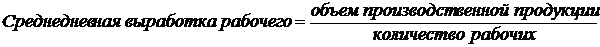
По первому цеху расчет производим по средней арифме­тической взвешенной:

 

 

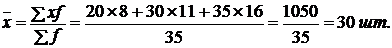
По второму цеху —по средней гармонической взвешенной:

 

 

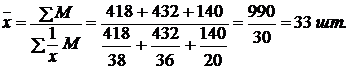
Пример 5. Имеются следующие данные о распределении ра­бочих по тарифному разряду:

Тарифный разряд, х	Число рабочих, в % к итогу, f	Сумма накопленных частот, å f
Итого

 

Определите моду и медиану.

Решение. В дискретных рядах модой является варианта с наибольшей частотой. В задаче наибольшее число рабочих имеют четвертый разряд (49%). Следовательно, мода равна четвертому разряду. Для вычисления медианы надо опре­делить сумму накопленных частот ряда, составляющую по­ловину общей суммы частот. В графе 3 накопленная сум­ма частот составляет 63. Варианта х, соответствующая этой сумме, т. е. четвертому разряду, есть медиана.

Если сумма накопленных частот против одной из ва­риант равна половине суммы частот, то медиана определя­ется как средняя арифметическая этой варианты и после­дующей.

Пример 6. Имеются следующие данные о распределении ра­бочих по затратам времени на обработку одной детали:

Затраты времени на одну деталь, мин., х	Число рабочих, чел., f	Сумма накопленных частот, å f
4,5 – 5,5
5,5 – 6,5
6,5 – 7,5
7,5 – 8,5
8,5 – 9,5
9,5 – 10,5
10,5 – 11,5
Итого

 

Определите моду и медиану.

 

Решение. В интервальных рядах распределения с равны­ми интервалами мода (М_о) и медиана (М_е) определяются по формулам:

 

 

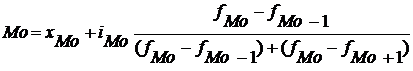
где 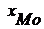= 7,5 – начальное значение модального интервала;

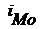= 1 – величина модального интервала;

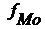= 30 – частота модального интервала;

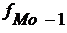= 23 – частота интервала, предшествующего модальному;

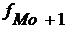= 12 – частота интервала, следующего за модальным.

 

Следовательно,

 

 

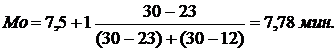
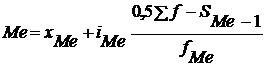
где 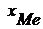= 7,5 – тачальное значение интервала, содержащего медиану;

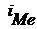= 1 – величина медианного интервала;

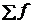= 100 – сумма частот ряда;

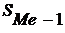= 49 – сумма накопленных частот, предшествующих медианному интервалу;

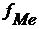= 30 – частота медианного интервала.

Следовательно,

 

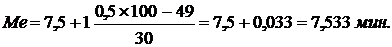
Таким образом, одна половина рабочих затрачивает на обработку детали до 7,53 мин., другая – свыше 7,53 мин.