Из этих двух свойств  следует, что

(формула 3.32)

в частности, если  п = 1 и a_i = 0 то

(формула 3.33)

Таким образом,  если входное воздействие на систему отсут­ствует, то и реакция системы равна будет равна нулю.

Оператор L_H  называется линейным неоднородным, если он состоит из линейного однородного оператора и некоторой вполне определенной неслучайной функ­ции  

(формула 3.34)

Будем называть систему нелинейной и обозначать ее S_n если оператор этой системы является нелинейным. ( N )Если оператор системы линейный ( L ), то систему будем называть ли­нейной и обозначать S_L .

Линейные системы S_L играют значительную роль в инженерных приложениях. Оператор системы S во мно­гих случаях может быть либо строго линейным, либо линеаризуемым.

На рисунке  3.4 показана зависимость ско­рости вращения вала турбо­реактивного двигателя в зависимости от количества подаваемого топлива х. В диапазоне «рабочих» зна­чений величины (а, b ) функция у(х) может быть линеаризована или представлена рядом прямых (ломаной). Практически анализ линейных систем выполняется легче, чем анализ нелинейных систем.

Рисунок 3.4

Здесь имеется определенная аналогия с функция­ми случайных величин. Известно, что чис­ловые характеристики линейной функции случайных величин определяются через числовые характеристики аргументов. Если случайная величина

то

 

где

 

Ранее  было показано, что случайный  процесс  X ( t ) может быть с достаточной точностью представлен своим канони­ческим разложением

 

(формула 3.35)

Этот случайный процесс X ( t ) подается на вход линейной системы S_L

имеющей линейный неоднородный оператор L_H

Рисунок 3.4

Следовательно, случайный процесс X(t) подвергнется
линейному неоднородному преобразованию (3.34):

 

(формула 3.36)

В соответствии с первым свойством линейного одно­родного оператора (3.30) получаем:

(формула 3.37)

Так как случайная величина  V _k не зависит от времени t, по которому проводится линейное однородное преобразование, то эту случайную величину можно вынести за знак линейного однород­ного оператора:

 

Обозначим

(формула 3.38)

                 

 (формула 3.39)

Тогда получим

 

 

(формула 3.40)

Выражение (3.40) представляет собой канониче­ское разложение случайного процесса  Y ( t ), у которого:

1. Математическое ожидание

(формула 3.41)

2. Координатные функции определяются из выражения(3.38)

 

 

3. Коэффициенты разложения

остались без изменения, следовательно

(формула 3.42)

Таким образом, можно сформулировать следую­щее правило неоднородного линейного преобразова­ния случайного процесса заданного своим каноническим разложением (3.35)

Если случайный процесс, за­данный своим каноническим разложением

       

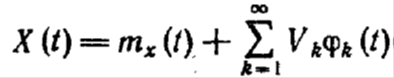
подвергнут  линейному  неоднородному преобразованию L_H ,    то получится случай­ный процесс тоже в виде канонического разложения:

при этом математическое ожидание случайного процесса Y ( t ) получается в результате того же линейного неоднородногопреобразования математического ожидания случай­ного процесса X ( t ):

                          

а координатные функции канонического разложения случайного процесса Y ( t ) получаются в результате соответствующего линейного однородного преобразо­вания координатных функций канонического разложе­ния случайного процесса X ( t ):

                            

коэффициенты канонического разложения случайного процесса Y(t)остаются теми же, что коэффициенты канонического разложения случайного процесса X(t).

Так как случайный процесс Y(t) представлен своим канониче­ским разложением

то  и его корреляционная функция может быть также представлена каноническим разложением:

(формула 3.43)

В  соответствии с равенствами (3.38)  и (3.39) выраже­ние (3.43) можно записать в виде

 

(формула 3.44)

В этом выражении   означает, что линейный однородный оператор берется по аргументу t, а     аргументу t'.

Применяя к выражению (3.44)  первое свойство линейного однородного оператора, получим

 

 

 

Выражение, стоящее под знаком суммы, представ­ляет собой корреляционную функцию случайного процесса X(t), сле­довательно,

 

 

Так как корреляционная  функция симметрична относительно своих аргу­ментов, то

(формула 3.45)

Таким образом, корреляционную функцию K_y ( t , t ') случайного процесса Y ( t ) , полученного в результате линейного неоднородного преобразования случайного процесса X ( t ): Y ( t ) = L_H { X (t) } , можно найти в ре­зультате соответствующего двойного линейного одно­родного преобразования корреляционной функции K_x ( t , t ') случайного процесса X ( t ) , взятого сначала по аргументу t , а затем - по t ' (или наоборот).

Так как дисперсия D_y ( t ) случайного процесса Y ( t ) равна его корреляционной  функции при равенстве аргументов, то

(формула 3.46)

Следовательно, дисперсия D_y ( t ) случайного процесса Y (у) , полученного в результате линейного неоднород­ного преобразования случайного процесса X ( t ):Y(t) =L_H{X(t)}, получается в результате двукратного применения соответствующего линейного однородногопреобразования к корреляционной функции K_x ( t , t ') и затем нахождения предела полученного выражения при t - t'.

Таким образом, схема решения задачи линейного преобразования случайного процесса X ( t ) следующая:

· даны характе­ристики преобразуемого случайного процесса X ( t ) (математическое  ожидание m_x ( t ) и корреляционная функция K_x ( t , t ').  

· задано линейное неоднородное преобразование

Требуется найти характеристики случайного процесса Y(t) (математическое ожидание m_y ( t ) и корреляционную функцию K _y (t,t') . )

В соответствии с равенствами (3.41) и (3.44) получаем

 

(формула 3.47)

 

Особо отметим, что указанная схема имеет место как для случая, когда случайный  процесс Х( t ) задан своим каноническим разложением, так и для случая, когда неизвестно каноническое разложение случайного процесса Х( t ) Это следует из того, что практически любой случайный процесс может быть с достаточной точностью представлен своим каноническим разложением.

Проведем  анализ нелинейного преобразования  случайного процесса Х( t ), заданного своим каноническим разложением:

где N_t { X ( t )} -нелинейный оператор от функции X ( t )по аргументу t.

Нелинейные операторы N_t {X( t )} не обладают общими свойствами, которыми обладают линейные операторы L _t {X(t)} Каждый нелинейный оператор N_t {X( t )}обладает своими свойствами. Поэтому общих правил нахождения характеристик случайного процесса, полученного в результате преобразования случайного процессаX ( t ) нелинейной системой S _n, нет.

Однако и в этом случае можно утверждать, что случайный процесс. Y ( t ) на выходе нелинейной системы S _n, тоже можно представить в виде канонического разложения, параметры которого: математическое  ожидание. m_v ( t ), координатные функции и коэффициенты разложения будут зависеть от параметров канонического разложения случайной функции X ( t ), подаваемой на вход нелинейной системы S _n и оператора этой системы Nt { X ( t )}.Это утверждение следует из того, что с достаточной точностью любой случайный процесс можно представить в виде канонического разложения.