Движения, описываемые линейным дифференциальным уравнением с постоянными коэффициентами

Весьма часто в физике вообще и в механике в частности возникают обыкновенные линейные дифференциальные уравнения с постоянными коэффициентами.

 

Определение 5.1 Обыкновенным однородным линейным дифференциальным уравнением n -порядка с постоянными коэффициентами называется уравнение вида:        (5.9) где an, an-1, …, a0 – числа .

Простым примером такого уравнения может служить второй закон Ньютона в рассмотренном случае движения тела под действием силы вязкого трения (5.3). Решение уравнения вида (5.9) удобно искать в виде экспоненты – функции, производная которой отличается от нее самой на константу:

  (5.10)

Подстановка пробного решения (5.10) в уравнение (5.9) превращает его в алгебраическое уравнение вида:

                                 (5.11)

называемое характеристическим уравнением.

В общем случае алгебраическое уравнение n-степени имеет n различных корней: λ₁, λ₂, …, λ_n. Случаи случайно совпадающих – «вырожденных» корней будут обсуждаться позже. С помощью совокупности найденных корней можно построить набор из n линейно-независимых решений вида C_jeхр(λ_jt) уравнения (5.9). В силу линейности последнего сумма решений так же является решением уравнения, которое зависит от n произвольных констант и называется общим решением однородного дифференциального уравнения (5.9):

                                          (5.12)

    Из математики известно, что некоторые корни алгебраического уравнения (5.11) могут оказаться комплексными.

 

Определение 5.2 Комплексными числами называются упорядоченные пары действительных чисел вида z = z ’ + iz ’’, для которых определены операции сложения и умножения на число: . (5.13)

 

Из определений (5.13) в частности следует, что i² = i·i = -1. Так введенный математический объект «i» называют мнимой единицей.

Для перехода от формально получаемых по описанной процедуре (5.10) – (5.12) комплекснозначных решений к физически осмысленным вещественным весьма полезны формулы Эйлера.

 

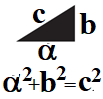
Теорема 5.1. Формулы Эйлера Экспоненциальная функция от чисто-мнимого аргумента выражается через тригонометрические функции согласно соотношениям: .          (5.14)

Доказательство формул Эйлера не может быть выполнено абсолютно строго, поскольку в математике соотношения (5.14) принято рассматривать как определение экспоненциальной функции от комплексного аргумента и доказывается, что такая функция обладает всеми «привычными» свойствами экспоненты от аргумента вещественного. Тем ни менее на «физическом уровне математической строгости» могут быть представлены следующие «правдоподобные» соображения.

       Одним из возможных определений экспоненты является утверждение о том, что эта функция, равная своей производной для всех значений ее аргумента: de^x/dx = e^x. Очевидно, что это свойство должно сохраняться и в случае обобщений на случай чисто мнимых значений x = iφ: de^iφ/d(iφ) = e^iφ. Дифференцирование тригонометрического представления экспоненциальной функции от чисто мнимого аргумента демонстрирует полностью аналогичное поведение производной:

Из равенства производных двух функций еще не следует равенство между ними: функции могут отличаться на константу. Однако при φ=0 любое из равенств (5.14) обращается в тождество, т.е. значение константы является нулевым. В качестве дополнительного аргумента в пользу справедливости формул Эйлера может быть приведен факт равенства в нуле производных любого порядка от правых и левых частей любого из равенств (5.14), в чем легко убедиться с помощью простых вычислений.

 

Пример 5.3. Свободные незатухающие колебания пружинного маятника Груз массой m , прикрепленный к вертикальной стенке идеальной пружиной жесткости k, расположен в точке устойчивого равновесия на гладкой горизонтальной поверхности (рис.5.3). Описать движение груза, если известно, что в начальный момент времени t =0 ему сообщили начальную скорость v0, направленную в направлении точки крепления пружины.

Решение. Проектирование уравнения движения (5.4) на горизонтальную ось, направленную вдоль вектора начальной скорости приводит к обыкновенному линейному однородному дифференциальному уравнению второго порядка:

                                                   (5.15)

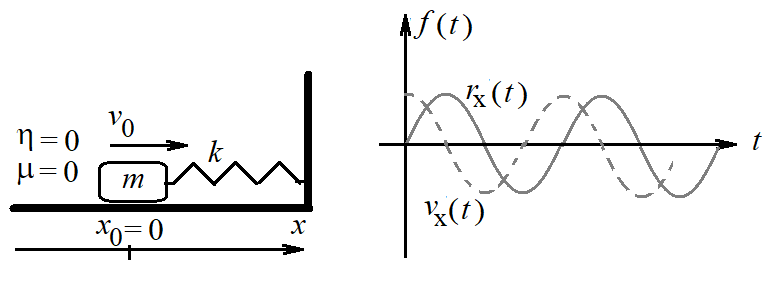
Рис. 5.3.  Идеальный пружинный маятник
и его свободные незатухающие колебания

 

       Подстановка в (5.15) пробного решения в виде экспоненты (5.10) приводит характеристическое уравнение (5.11) к простейшему виду квадратного уравнения, имеющего два чисто мнимых корня:

                                                  (5.15)

Общее решение однородного дифференциального уравнения (5.12) зависит от двух констант, значения которых однозначно определяются из двух начальных условий: r_x(0) = 0 и v_x(0) = v₀. В результате возникает решение в виде незатухающих гармонических (синусоидальных) колебаний на собственной частоте ω₀ = (k/ m)^1/2:

                   (5.16)

Обязательно выполните самостоятельно все пропущенные выкладки! Помните, что существует лишь один способ научиться решать дифференциальные уравнения (и брать интегралы): решать эти уравнения (и вычислять интегралы) самостоятельно. J

 

Определение 5.2 Обыкновенным неоднородным линейным дифференциальным уравнением n -порядка с постоянными коэффициентами называется уравнение вида:  (5.17 ) где an , an -1 , …, a 0 – числа, а F ( t ) – известная (заданная) функция.

       Зависящее от n произвольных констант (необходимых для удовлетворения n начальным условиям) общее решение неоднородного уравнения следует искать в виде суммы общего решения соответствующего однородного уравнения (5.9), содержащего нужное число произвольных констант, и частного (т.е. какого угодно) решения неоднородного уравнения:

 

             (5.18 )

 

Легко убедиться, что подстановка (5.18) превращает (5.17) в верное тождество. Универсальный метод нахождения общего решения однородного уравнения (5.9) – (5.12) уже был рассмотрен. Частное решение из (5.18) нередко удается найти методом угадывания. Позже будут рассмотрены более удобные и надежные методы нахождения частных решений неоднородных уравнений.

    Способный вызвать недоумения некоторый произвол, допущенный в виде выбора вида решений дифференциальных уравнений (5.9) и (5.17) не должен вызывать сомнений в правильности полученных описанными способами решений в силу теоремы единственности решения задач механики.

Весьма простым примером такого уравнения может служить второй закон Ньютона в рассмотренном случае падения тела в вязкой среде (5.3).

 

Пример 5.4. Вынужденные колебания пружинного маятника Груз массой m, прикрепленный к вертикальной стенке идеальной пружиной жесткости k, расположен в точке устойчивого равновесия на гладкой горизонтальной поверхности (рис.5.3).Описать движение груза, если известно, что в начальный момент времени t =0 на него начала действовать направленная вдоль пружины внешняя сила, изменяющаяся во времени по гармоническому закону: F ( t )= F 0 sin (ω t ).

s

Решение. Проектирование уравнения движения (5.4) на горизонтальную ось, направленную вдоль вектора начальной скорости приводит к обыкновенному линейному неоднородному дифференциальному уравнению второго порядка:

                          (5.19)

Зависящее от двух произвольных констант общее решение соответствующего (5.19) однородного уравнения может быть записано как в экспоненциальном, так и в тригонометрическом виде:

где подлежащие определению из начальных условий постоянные A₀ и φ₀, называются соответственно вещественной амплитудой и фазой свободных колебаний_-.

           Частное решение неоднородного уравнения (5.19) разумно искать в виде синусоидальной функции с частотой, равной частоте вынуждающей силы:

 

                                       (5.20 )

Подстановка пробного решения (5.20) в уравнение (5.19) позволяет найти амплитуду вынужденных колебаний и построить частное решение неоднородного уравнения:

В результате общее решение неоднородного уравнения (5.19) имеет вид:

         (5.21)

 

После нахождения входящих в (5.21) произвольных констант А₀ и φ₀ из начальных условий окончательное решение принимает вид:

 

                   (5.22)

 

Используя разобранный пример вынужденных колебаний идеального пружинного маятника, целесообразно перечислить общие особенности поведения линейных систем вблизи состояний их устойчивого равновесия при внешних воздействиях на них.

При отсутствии внешних воздействий система покоятся в одной из точек устойчивого равновесия или совершают колебания вблизи нее. В случае малых амплитуд колебания оказываются практически гармоническими. При внешнем воздействие отклик системы представляет собой суперпозицию (сумму) гармонических колебаний (5.22) на собственной частоте системы и частоте вынуждающей силы (рис. 5.4.a). При несовпадении частоты собственных колебаний и вынуждающей силы возникают биения – негармонические колебания, амплитуды которых периодически усиливается и ослабевает в зависимости от того, как происходит наложение двух решений: в фазе или противофазе:

                     (5.23)

Рис. 5.4. Особенности вынужденных колебаний линейной системы на примере пружинного маятника без трения

 

       Важной особенностью вынужденных колебаний (5.23) является наличие сильной зависимости амплитуды А от частоты (рис.5.4.б). При приближении частоты вынуждающей силы к собственной резонансной частоте системы происходит резкое возрастание амплитуды вынужденных колебаний, называемое резонансом. В рассматриваемом случае при совпадении частот амплитуда оказывается бесконечно большой, что соответствует неограниченному раскачиванию системы внешней силой, сопровождается линейным по времени ростом амплитуды колебаний (рис. 5.4.в):

 

                         (5.24)

В реальности никакого неограниченного возрастания амплитуды не наблюдается. Включение в модель (5.19) всегда имеющихся в механических системах диссипативных сил в виде линейной по скорости силы вязкого трения приводит к экспоненциальному затуханию собственных (5.21) колебаний системы. При этом переходный режим (5.22) с биениями (5.23)оказывается ограниченным во времени и постепенно сменяется стационарным  режимом  гармонических колебаний на частоте вынуждающей силы.

Резонансные кривые при учете затухания перестают претерпевать разрывы, амплитуда вынужденных колебаний всегда остается ограниченной. В случае точного резонанса формула (5.24) видоизменяется так, что  амплитуда эффективно раскачивающихся колебаний со временем возрастает, асимптотически выходя на стационарное значение.

  

5.5. Движение, описываемое нелинейным дифференциальным
уравнением (реальный маятник)

При решении задач на расчет движения систем, описываемых нелинейными уравнениями, как правило, приходится использовать численное интегрирование уравнения движения. Идея приближенного численного решения основной задачи механики состоит в аппроксимации реального движения материальной точки на небольшом интервале времени движения Δt_j = t_j+1 - t_j и, следовательно, малом участке траектории Δr(t_j) более простым движением, например равноускоренным. В этом случае силу, действующую на тело на каждом небольшом участке Δr(t_j), можно считать приближенно постоянной. Используя известные формулы равноускоренного движения (2.13), и (2.14) и известные значения сила (а, следовательно, и ускорения) на рассматриваемом участке легко рассчитать новые значения скорости v(t_j+1) и радиус-вектора r(t_j+1) в конечной точке этого участка, являющегося начальным для следующего. По новым значениям времени, радиус-вектора тела и его скорости вычисляется сила, действующая на следующем участке F(t_j+1, r_j+1, v_j+1) и ускорение на нем, что дает возможность приближенного расчета перемещения и приращения скорости на следующем интервале времени:

       (5.25)

    Точность описанного алгоритма возрастает с уменьшением интервалов времени Δt_j, что приводит к необходимости выполнения больших объемов простых и однотипных вычислений, для которых естественно использование компьютеров. Алгоритм (5.25), по сути обеспечивающий аппроксимацию реальной траектории участками парабол, не является оптимальным с точки зрения соотношения «точность/объем вычислений». На практике при решении уравнений движения (и других задач физики) сегодня наиболее популярным является метод Рунге-Кутта четвертого порядка, аппроксимирующий траекторию полиномами более высокой, чем вторая, степени
 (http://www.math.spbu.ru/user/pan/Page8-cauchy.pdf).

 

 

Пример 5.5. «Реальные» колебания математического маятника Точечный груз массой m , прикреплен к точечной опоре невесомым стержнем длиной R (рис. 5.5) и находится в точке минимума его потенциальной энергии. Описать движение груза, если ему сообщили начальную горизонтальную скорость v 0.

Решение. В случае математического маятника удобной характеристикой положения груза является угол между вертикалью и нитью (рис. 5.5). Соответствующее уравнение движения имеет вид:

                                                                         

который удобно переписать в стандартных обозначениях:

                                            (5.26)

Решение уравнение 5.26 при начальных скоростях, недостаточных для переворота маятника, представлено на графиках на рис. 5.5. При малых начальных скоростях колебания практически неотличимы от гармонических мз-за того, что при малых углах синус может быть аппроксимирован линейной функцией, что приводит уравнение (5.26) к виду (5.15). При увеличении начальной скорости период колебаний заметно увеличивается, что нехарактерно для линейного осциллятора….

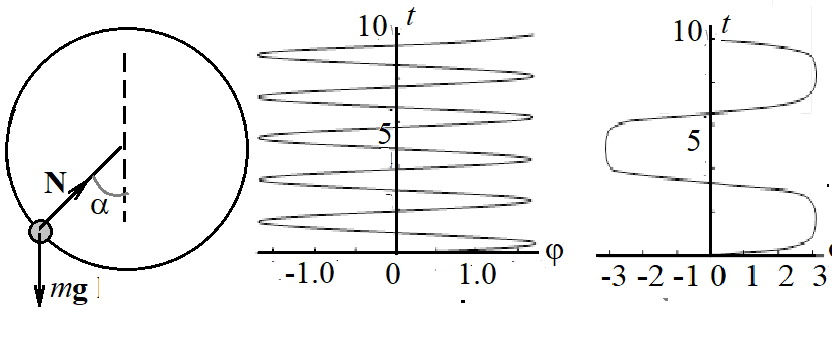
Рис. 5.5.Колебания маятникапри малых начальных скоростях, недостаточных для совершения переворотов

При еще больших значениях начальной скоростей маятник начинает делать полные перевороты (рис. 6). При дальнейшем увеличении начальной скорости все меньшую роль торможение маятника гравитационными силами. В пределе больших скоростей маятник будет почти равномерно вращаться в вертикальной плоскости.

Рис. 5.6.Перевороты маятникапри достаточно
больших начальных скоростях

Вопросы и задачи для самостоятельной работы

1. Решить задачу о зависимости от времени координаты тела, движущегося пол действием силы вязкого трения, величина которой зависит от скорости по квадратичному закону:

Построить графики зависимости от времени координаты, скорости и ускорения тела, падающего с вязкой среде.

2. Решить задачи о торможении тела и о  падении тела в линейной вязкой среде (см. Примеры 5.1 и 5.2), используя стандартные методы решения линейных дифференциальных уравнений с постоянными коэффициентами.

3. Решить задачу об одномерном движении тела под действием упругих сил в случае произвольных начальных условий (v0 ¹ 0, x0 ¹ 0). Попытайтесь получить графики зависимости от времени координаты и скорости частицы при различных начальных условий, решая дифференциальное уравнение движения при помощи какого-либо стандартного математического пакета.

4. Вблизи точек неустойчивого равновесия действующая на тело сила может быть приближенна задана (постарайтесь досуматься, почему?) в виде f = + kx, где k – «коэффициент антиупругости» ( J ). Решите уравнение движения и опишите поведение тела, находившегося в точке неустойчивого равновесия, если ему сообщена начальная скорость v₀.

5. Пружинный маятник, испытывавший действие внешней гармонической силы с частотой ω, совершал вынужденные колебания с амплитудой А на частоте вынуждающей силы. После того, как частота вынуждающей силы была увеличена в n = 2 раза, амплитуда вынужденных колебаний в стационарном режиме возросла в m раз. Чему равна собственная частота колебаний пружинного маятника?

6. Тело массой М подвешено к потолку на невесомой нерастяжимой нити длиной L и равномерно вращается по круговой траектории. Найти зависимости периода обращения тела от угла, который нить составляет с вертикалью.

7. Найдите период малых колебаний поплавка цилиндрической формы с заданными размерами, плавающего на поверхности жидкости. Плотности жидкости и поплавка заданы.

8. На невесомой нити длиной L подвешен неподвижный точечный груз массы m. Точку подвеса начинают перемещать горизонтально с постоянным ускорением  . Найти период и амплитуду возникших малых колебаний.

9. Обруч радиуса R расположен вертикально.  На обруч надета бусинка в виде небольшого шарика массой m, совершающая вблизи нижней точки обруча малые гармонические колебания. С каким постоянным вертикальным ускорением нужно двигать обруч для того, чтобы частота малых колебаний бусинки была в 2 раза меньше?

10. Повторите решение, разобранное в Примере 5.4 для случая, когда внешняя сила изменяется во времени по закону F= F₀ cos(ωt).

11. Попытайтесь повторить решение, разобранное в Примере 5.3 для случая, если на груз помимо силы упругости действует сила вязкого трения, зависящая от скорости по линейному закону.

12. Небольшое тело массой m бросили вертикально верх со скоростью v₀ в жидкости, плотность которой в 2 раза меньше плотности тела. Во сколько раз отличаются время подъема тела и время его падения обратно в точку бросания, если на него кроме силы тяжести действует линейная по скорости сила трения? Коэффициент вязкого трения η известен.

Лекция 6