Стандартные задачи с нестандартными решениями.

Носова Л.И.

В распоряжении учителя имеется достаточное количество нестандартных задач, однако в большинстве случаев они рассчитаны на внеурочные занятия, в связи, с чем для непосредственного использования на уроках могут оказаться слишком трудными, либо не имеющими органической связи с изучаемым материалом. В то же время существуют задачи, которые можно решать как стандартным, так и не стандартным способом. Эти задачи всегда органически связаны с изучаемым материалом; кроме того, допуская нестандартное решение, приучают школьников не довольствоваться шаблоном, нацеливают на вдумчивый подход, воспитывают стремление как можно лучше выполнить порученное дело.

Общие задачи с нестандартным решением полезно решать на материале любого класса. Особенно это уместно на уроках повторения. В ряде случаев они уже давно находят применения в школьной практике, в частности при обучении приемам устного счета. Сюда можно отнести упражнения на применении законов действий и признаков делимости (например: 428*75=107*4*25*3=321*100=32 100), особые случаи нахождения нескольких процентов от числа (10%, 25%, 33 %, 12,5% и т.п.), применение формул сокращенного умножения (47²=(50-3)²=2500-300+9=2209;899=30²-1²=29*31), извлечение корня ( = =105).

Рассмотрим теперь ряд примеров, не получивших еще должного применения в практике преподавателя.

1. Среди упражнений со скобками на выполнение арифметических действий следует время от времени использовать примеры, где вычисление целесообразно начинать не с первой скобки. Например:

а) ;

б) .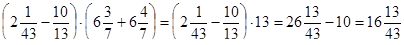

2. Среди упражнений на сложение и вычитание обыкновенных дробей должны встречаться и такие, где уместен отказ от приведения дробей к общему знаменателю. Например:

            .

3. При упрощении выражений вида   обычно числитель и знаменатель умножают на сопряженное знаменателю выражение, поэтому полезно рассмотреть один - другой пример такого же вида, допускающий нестандартное решение:

а) .

б) .

4. Уравнения   и  очень похожи одно на другое. Их можно решать стандартным способом сведения к квадратному уравнению. Однако нетрудно заметить, что второе уравнение допускает и нестандартное решение: его корни х₁=3 и х₂=  очевидны. А поскольку всякое квадратное уравнение имеет не более двух корней, то на этом решение и заканчивается. Через некоторое время можно предложить учащимся уравнение , при решении которого указанный прием применяется в усложненном виде: прибавив к обеим частям уравнения по 3, легко обнаружить, что  или , т.е. х₁=2, х₂= .

5. При решении иррационального уравнения учащихся, прежде всего, начинают «уединять» радикал, «возводить» обе части уравнения в степень и т.д., тогда как нередко в этом нет никакой необходимости, особенно в тех случаях, когда уравнение не имеет решений или имеет только одно решение, которое к тому же легко отыскивается подбором. Поэтому наряду с уравнениями, требующими стандартного подхода, должны быть и, например, такие:

а) ;

б) ;

в) .

Прежде чем непосредственно приступить к решению уравнения такого рода, ученик должен всмотреться в него, проследить поведение отдаленных членов уравнения при допустимых значениях неизвестного. Так, в первом из данных уравнений второй радикал имеет смысл при , тогда как первый радикал при этих значениях 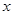смысла не имеет, т.е. уравнение не определено ни при каких значениях .

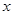Второе уравнение определено при 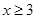, однако нетрудно видеть, что при указанных значениях 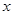левая часть уравнения больше 5, т.е. она не может равняться правой части.

Наконец, в третьем уравнении, которое определено при ,левая часть отрицательна и не может быть равной неотрицательной правой части.

6. При решении некоторых уравнений и неравенств нестандартное решение иногда становится возможным на основе следующего факта: монотонная функция каждое свое значение принимает только один раз.

Рассмотрим уравнение . Функция  возрастающая на всей области определения (т.е. при ), так как она является суммой двух возрастающих функций. Следовательно, эта функция значение 4 может принять не более одного раза. Легко заметить, что такое значение она принимает при . Итак, данное уравнение имеет единственный корень .

Еще более убедительно выглядит рациональность рассмотренного приема на примере уравнения . Переписав его в виде , легко приходим к очевидному единственному решению .

7. Путем аналогичных рассуждений получим, что каждое из уравнений 2^х+4^х=20 и 2^х+3^х=13 имеет единственное решение , хотя первое из них можно решить и стандартным способом, сведя его к квадратному относительно 2^х.

8. Неравенства  и  при поверхностном взгляде представляются однотипными и могут быть решены обычным стандартным способом. Однако второе из них можно решить и с помощью свойства монотонной функции. Действительно, переписав его в виде , мы получим в левой части неравенства возрастающую функцию , определенную при . Теперь не так уж трудно заключить, что неравенство выполняется при .

Попутно отметим, что оба неравенства легко могут быть решены графически (рис.1 и 2).

Рис. 1                                                                                  Рис. 2

9. Графическое решение бывает иногда уместным и в тех случаях, когда стандартное решение выходит за рамки школьной программы. Пусть требуется вычислить интеграл . Учащиеся не умеют находить первообразную для данной подынтегральной функции, следовательно, стандартное решение по формуле Ньютона-Лейбница осуществить не могут. Однако графическое представление подынтегральной функции сразу ведет решение задачи. Действительно, если , то , т.е. . Поскольку , то графиком подынтегральной функции является верхняя полуокружность с центом в точке (2;0) и радиусом 3 (рис. 3). Итак, искомый интеграл равен .

                                                                                       Рис. 3

Одним из довольно распространенных недостатков при повторении материала является полное копирование того пути, который был ранее использован при первом знакомстве с этим материалом, что, конечно, не вызывает у школьников особого интереса. Поэтому заслуживают внимания уместные отклонения от «стандарта» посредством интересных сопоставлений, взаимосвязей, обобщений. В качестве примера остановимся на повторении в ХI классе темы «Решение прямоугольных треугольников». Его целесообразно начать с задачи, которая вызвала живую реакцию учащихся, например:

Доказать, что сумма синусов острых углов прямоугольного треугольника всегда больше единицы.

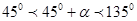Как правило, учащиеся дают следующее решение. Пусть - один из острых углов прямоугольного треугольника, тогда второй угол равен . Далее имеем ,так как если , т.е. , то .

Однако такое решение учителя не удовлетворяет. Он просит вспомнить, как определяется синус угла прямоугольного треугольника через катет и гипотенузу. Через некоторое время учащиеся с радостным удивлением обнаруживают чрезвычайно простое решение: если a, b, c – соответственно катеты и гипотенуза прямоугольного треугольника, сумма синусов острых углов равна (так как сумма катетов больше гипотенузы). После этого учащиеся более серьезно отнесутся к заданию учителя повторить к следующему уроку соотношение между сторонами и углами прямоугольного треугольника.

Посредством оригинальных упражнений и нешаблонных вопросов уроки повторения можно сделать столь же интересными, как и уроки по изучению нового материала.