Распространение тепла в неограниченном стержне. Фундаментальное решение уравнения теплопроводности

Для решения краевых задач математической физики широко применяется преобразование Фурье. Причина этого заключается в том, что образ Фурье искомой функции часто удовлетворяет более простому уравнению, чем сама искомая функция. При решении краевых задач математической физики преобразование Фурье используется по следующей схеме:

1. Подвергают преобразованию Фурье обе части уравнения, которому удовлетворяет искомая функция; отсюда получают уравнение для ее Фурье-образа;

2. Из этого уравнения находят образ Фурье искомого решения первоначального уравнения;

3. Используя обратное преобразование Фурье находят искомую функцию.

Рассмотрим распределение температуры в неограниченном в обе стороны прямолинейном стержне в произвольный момент времени 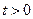, если ее распределение в начальный момент времени  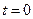известно. Стержень считаем теплоизолированным от окружающей среды по боковой поверхности и его сечение считаем настолько малым, что всем точкам сечения в каждый момент времени можно приписать одну и ту же температуру.

Задача заключается в нахождении решения уравнения теплопроводности в бесконечной области по известному начальному условию:

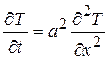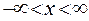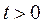, , ,                                             (1.2)

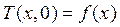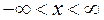, ,                                               (1.3)

где 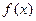 – заданная функция, абсолютно интегрируемая на оси .

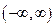Решаем эту задачу, применяя преобразование Фурье по переменной x. Обозначим через 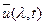 образ Фурье функции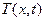

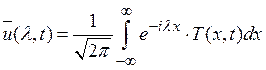.                                         (1.4)

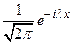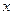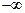Умножим обе части уравнения (1.2) на  и проинтегрируем по  от  до 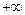, предполагая, что функция  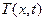и ее производные достаточно быстро стремятся к нулю при 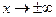. Интегрируя левую часть, получим

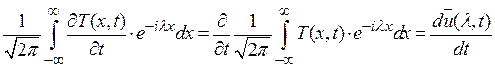.        (1.5)

Для преобразования правой части уравнения используем интегрирование по частям:

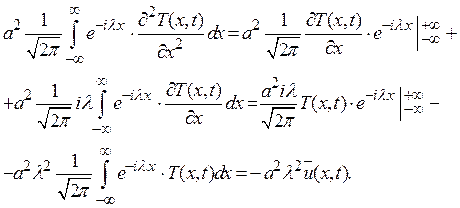         (1.6)

При получении (1.6) учли, что неинтегральные члены обращаются в нуль, в силу ограниченности функции 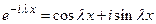 и предполагаемого поведения функции :

.

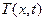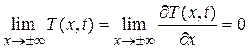Приравнивая (1.5) и (1.6), получим обыкновенное дифференциальное уравнение для образа Фурье искомой функции

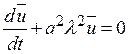.                                       (1.7)

Начальное условие для функции 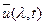 получим из начального условия (1.3), выполнив преобразование Фурье

,

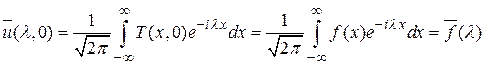 (1.8)

.

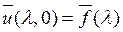Разделяя переменные в уравнении (1.8), получаем

,    .

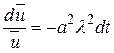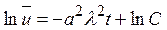Отсюда

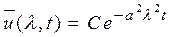.                                                    (1.9)

Определим постоянную С с помощью начального условия (1.8)

.

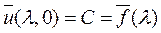Подставив это значение С в равенство (9), получим для Фурье-образа искомой функции следующее выражение

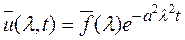.                                    (1.10)

Теперь осталось перейти к третьему этапу решения задачи - найти саму функцию 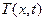 по найденному ее образу Фурье (1.10). Для этого применим к равенству (1.10) обратное преобразование Фурье, подставив вместо  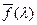его явное выражение из (1.8). Умножив (1.10) на  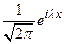и интегрируя по 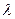, получаем

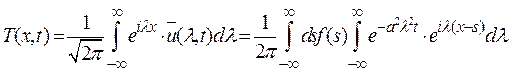.      (1.11)

Подставим в правую часть выражение для экспоненты с мнимым аргументом по формуле Эйлера

.

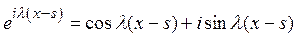Учитывая, что

,

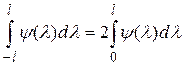если 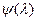 - четная функция, а также равенство ,

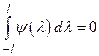если 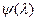 - нечетная функция, имеем

, .

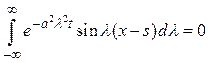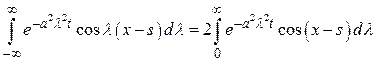Последний интеграл является известной и часто встречающейся в теории теплопроводности и теории диффузии функцией. Воспользуемся формулой

.

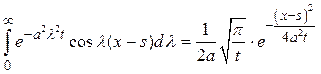Подставив эти результаты в выражение (1.11), получим решение уравнения (1.2) при начальном условии (1.3)

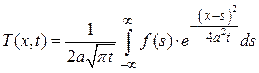 .                                        (1.12)

Формулу (1.12) называют формулой Пуассона. Функция аргументов 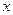 и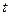

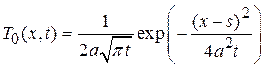                                   (1.13)

называется фундаментальным решением уравнения теплопроводности (1.2). Она удовлетворяет уравнению теплопроводности. Решение уравнения теплопроводности с начальным условием 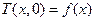 в виде (1.12) является сверткой фундаментального решения с начальной функцией.

Рассмотрим физический смысл фундаментального решения уравнения теплопроводности. Выделим малый элемент стержня 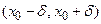 вблизи точки  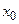и зададим начальное распределение температуры в виде

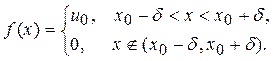
Физически это означает, что в начальный момент времени 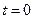 этому элементу стержня передали количества тепла  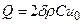( 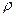- линейная плотность материала, 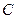- удельная теплоемкость), которое привело к повышению температуры на этом элементе на величину 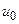. В последующие моменты времени распределение температуры в стержне определяется формулой (1.13), которая в данном случае принимает вид

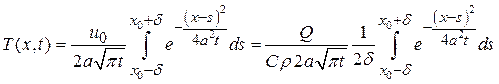
Если распределять то же самое количество тепла Q на все меньшем участке 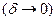, то в пределе в точке  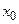стержню сообщается количества тепла Q. Это означает, что в точке  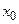стержня в момент  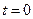действует мгновенный точечный источник тепла напряжения Q. От действия такого мгновенного точечного источника тепла в стержне получается распределение температур

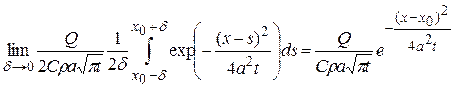,      (1.14)

где применена теорема о среднем для определенного интеграла

, .

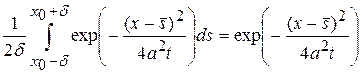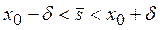Предел последнего выражения при 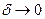, а значит 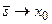, и приводит к выражению (1.14).

Итак, фундаментальное решение (1.13) дает распределение температуры, которое вызывается мгновенным точечным источником тепла напряжения 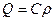, помещенным в начальный момент времени  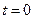в точке  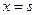стержня.

В соответствии с этим можно дать физическое толкование и решению (1.12). Для того, чтобы придать сечению 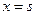 стержня температуру  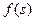в начальный момент времени, мы должны на малом элементе  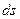около этой точки распределить количество тепла 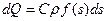, т.е. поместить в точке  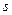мгновенный точечный источник тепла напряжения 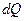. Распределение температуры, вызываемое этим мгновенным точечным источником будет равно

.

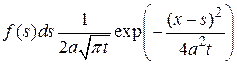Общее действие от начальной температуры 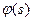 во всех точках стержня складывается от этих элементов, что и приводит к формуле (1.12).