 |
Главная |
Классификация численных методов
|
из
5.00
|
С помощью математического моделирования решение научно-технической задачи сводится к решению математической задачи, являющейся её моделью. Для решения математических задач используются следующие основные группы методов˸ аналитические, графические и численные.
При использовании аналитических методов решения задачи удается выразить с помощью формул. В частности, в случае если математическая задача состоит в решении простейших алгебраических или трансцендентных уравнений, дифференциальных уравнений и т.п., то использование известных из курса математики примеров сразу приводит к цели. К сожалению, на практике это бывает достаточно редко.
Графические методы позволяют в ряде случаев оценить порядок искомой величины. Основная идея этих методов состоит в том, что решение находится путем геометрических построений. Например, для нахождения корней уравнения f(x)=0 строится график функции y=f(x), точки пересечения которого с осью абсцисс и будут искомыми корнями.
Графически методы могут применяться для получения начальных приближений к решению, которые затем уточняются с помощью численных методов.
Основным инструментом для решения сложных математических задач в настоящее время являются численные методы, позволяющие свести решение задач к выполнению конечного числа арифметических действий над числами; при этом результаты получаются в виде числовых значений. Подчеркнем важные отличия численных методов от аналитических. Во-первых, численные методы позволяют получить лишь приближенное решение задачи. Во-вторых, они обычно позволяют получить решение задачи с конкретными значениями параметров и исходных данных.
Численные методы незаменимы в сложных задачах, которые не допускают аналитического решения.
Многие численные методы разработаны давно. С появлением ЭВМ начался бурный период их развития и внедрения в практику. Только ЭВМ под силу выполнить за короткое время объём вычислений в миллиарды, триллионы и более операций, необходимых для решения многих современных задач.
Численные методы наряду с возможностью получения результата за приемлемое время должны обладать и ещё одним важным качеством – не вносить в вычислительный процесс значительных погрешностей.
С некоторой степенью условности все численные методы можно разбить на следующие классы:
1) методы эквивалентных преобразований;
2) методы аппроксимации;
3) прямые методы;
4) итерационные методы;
5) методы статистических испытаний (методы Монте-Карло)
Дадим о них общее представление.
1. Методы эквивалентных преобразований. Эти методы основаны на замене исходной задачи другой, имеющей то же решение, но решающейся существенно проще.
Пример 1. Эквивалентное преобразование приведенного квадратного уравнения  с помощью выделения полного квадрата к виду
с помощью выделения полного квадрата к виду  сводит задачу к проблеме вычисления квадратного корня и приводит к известным формулам нахождения корней квадратного уравнения.
сводит задачу к проблеме вычисления квадратного корня и приводит к известным формулам нахождения корней квадратного уравнения.
Эквивалентные преобразования иногда позволяют свести решение исходной вычислительной задачи к решению задачи совершенно иного типа.
2. Методы аппроксимации. Эти методы позволяют приблизить (аппроксимировать) исходную задачу другой, решение которой в определенном смысле близко к решению исходной задачи. Погрешность, возникающая при такой замене, называется погрешностью аппроксимации. Как правило, аппроксимирующая задача содержит некоторые параметры, позволяющие регулировать величину этой погрешности или воздействовать на другие свойства задачи. Принято говорить, что метод аппроксимации сходится, если погрешность аппроксимации стремится к нулю при стремлении параметров метода к некоторым предельным значениям.
Пример 2. Учитывая определение производной  , для ее приближенного вычисления можно использовать формулу
, для ее приближенного вычисления можно использовать формулу  , где
, где 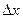 – параметр приближенной формулы. Погрешность аппроксимации стремится к нулю при
– параметр приближенной формулы. Погрешность аппроксимации стремится к нулю при  .
.
При решении нелинейных задач широко используются различные методы линеаризации, состоящие в приближенной замене исходной задачи более простой линейной.
3. Прямые методы. Метод решения задачи называется прямым, если после выполнения конечного числа элементарных операций он позволяет получить решение, которое при отсутствии ошибок округления будет точным.
Примером прямого метода может служить поиск корней квадратного уравнения по формулам.
Заметим, что элементарная операция прямого метода может на самом деле оказаться довольно сложной (вычисление значений специальной функции, решение системы уравнений и т.д.). То, что она принимается за элементарную, предполагает, что ее выполнение, по крайней мере, существенно проще вычисления решения всей задачи.
При построении прямых методов существенное внимание должно уделяться минимизации числа элементарных операций.
4. Итерационные методы. К ним относятся методы построения последовательных приближений к решению задачи. Применение метода начинается с выбора одного или нескольких начальных приближений. Каждое следующее приближение вычисляется по рекуррентным формулам с использованием найденных ранее приближений. Неограниченное продолжение этого итерационного процесса теоретически позволяет построить бесконечную последовательность приближений к решению – итерационную последовательность. Если эта последовательность сходится к решению задачи, то говорят, что итерационный метод сходится. Множество начальных приближений, для которых метод сходится, называется областью сходимости метода.
Пример 3. Требуется приближенно вычислить значение  на ЭВМ, способной выполнять лишь простейшие арифметические операции. Пусть
на ЭВМ, способной выполнять лишь простейшие арифметические операции. Пусть  – некоторое начальное приближение к
– некоторое начальное приближение к  . Для вычисления каждого следующего приближения построим рекуррентную формулу:
. Для вычисления каждого следующего приближения построим рекуррентную формулу:
 ,
,
называемой алгоритмом Герона. Известно, что данный итерационный метод сходится при любом начальном приближении  , так что область его сходимости – множество всех положительных чисел.
, так что область его сходимости – множество всех положительных чисел.
Вычислим с его помощью  с точностью до 8 значащих цифр, взяв
с точностью до 8 значащих цифр, взяв  . Последовательно получим
. Последовательно получим  ;
;  ;
;  ;
;  . У двух последних приближений совпали первые 8 цифр, следовательно,
. У двух последних приближений совпали первые 8 цифр, следовательно,  будем считать решением задачи.
будем считать решением задачи.
Практическая реализация итерационных методов всегда связана с необходимостью выбора критерия окончания итерационного процесса. Вычисления не могут продолжаться бесконечно долго и должны быть прерваны в соответствии с некоторым критерием, связанным, например, с достижением заданной точности.
5.  Метод Монте-Карло – это численный метод решения математических задач при помощи моделирования случайных величин. В подавляющем большинстве задач, решаемых методами Монте-Карло, вычисляют математические ожидания некоторых случайных величин. Так как чаще всего математические ожидания представляют собой обычные интегралы, в том числе и кратные, то центральное положение в теории методов Монте-Карло занимают методы вычисления интегралов.
Метод Монте-Карло – это численный метод решения математических задач при помощи моделирования случайных величин. В подавляющем большинстве задач, решаемых методами Монте-Карло, вычисляют математические ожидания некоторых случайных величин. Так как чаще всего математические ожидания представляют собой обычные интегралы, в том числе и кратные, то центральное положение в теории методов Монте-Карло занимают методы вычисления интегралов.
Пример 4. Предположим, что нам необходимо вычислить площадь плоской фигуры. Это может быть произвольная фигура, заданная графически или аналитически (связная или состоящая из нескольких частей). Пусть это будет фигура, заданная на рис. 2.1. Предположим, что эта фигура расположена внутри единичного квадрата.
Выберем внутри квадрата N случайных точек. Обозначим через N1 число точек, попавших внутрь фигуры. Геометрически видно, что площадь фигуры приближенно равна отношению N1/N. Причем, чем больше число , тем больше точность этой оценки.

Рисунок. 2.1. Вычисление площади фигуры методом Монте-Карло
Интерполяция функции
Одной из важнейших проблем вычислительной математики является приближение функций. Часто при решении прикладных задач приходится сталкиваться со следующей ситуацией. В результате расчета, эксперимента, опыта и т.д. получены значения некоторой функциональной зависимости.
Из теоретических соображений следует, что некоторая величина y является функцией f(x) непрерывного аргумента x, причем явный вид функции f(x) неизвестен. В то же время известно конечное количество значений функции yi на ограниченном интервале аргумента  в точках xi (i = 0, 1, ... , n). Эти точки xi (i = 0, 1, ... , n) называются узлами. Иначе говоря, исходная информация об исследуемой функции может быть записана в виде таблицы, содержащей n +1 упорядоченных пар чисел.
в точках xi (i = 0, 1, ... , n). Эти точки xi (i = 0, 1, ... , n) называются узлами. Иначе говоря, исходная информация об исследуемой функции может быть записана в виде таблицы, содержащей n +1 упорядоченных пар чисел.
| X | x0 | x1 | … | xn |
| Y | y0 = f(x0) | y1 = f(x1) | … | yn = f(xn) |
Пример графического изображения исходных данных таблицы приведен на рис. 2.2. Черными кружками обозначены значения yi функции f(x) в узлах интерполяции xi (i = 0, 1, ... , n).

Рисунок 2.2. Пример графика исходных данных, предназначенных для интерполяции.
Значения же функции в промежуточных точках неизвестны и их получение может быть связано с проведением сложных расчетов и экспериментов. В некоторых случаях даже при известной зависимости  ее использование в практических расчетах затруднительно из-за ее громоздкости (содержит трудно вычисляемые выражения, сложные интегралы и т.д.). Проблема заключается в вычислении значения функции y=f(x) для произвольного аргумента
ее использование в практических расчетах затруднительно из-за ее громоздкости (содержит трудно вычисляемые выражения, сложные интегралы и т.д.). Проблема заключается в вычислении значения функции y=f(x) для произвольного аргумента  , но не совпадающего ни с одним из узлов xi (i = 0, 1, ... , n).
, но не совпадающего ни с одним из узлов xi (i = 0, 1, ... , n).
Принцип интерполяции заключается в построении новой функции F(x), которая называется интерполирующей функцией или интерполянтом. Функция F(x) принадлежит к определенному классу и в точках xi (i = 0, 1, ... , n) принимает те же значения, что и функция f(x).
Рассмотрим случай, когда известны значения интерполируемой функции f(x). в равноотстоящих узлах. При этом узлы интерполяции xi выражаются формулой:
 (2.1)
(2.1)
Постоянный параметр h называется шагом интерполяции. В такой задаче исходными данными являются (n + 3) чисел: начальный узел интерполяции x0, шаг интерполяции h и (n + 1) значений неизвестной функции yi (i = 0, 1, ... , n) в узлах интерполяции.
Будем строить полином Pn(x) степени n
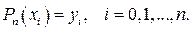 (2.2)
(2.2)
где значения xi заданы формулой (2.1). Полиномы для интерполяции по равноотстоящим узлам впервые были построены И.Ньютоном.
Первый полином Ньютона строится в форме:
 (2.3)
(2.3)
или в развернутом виде:
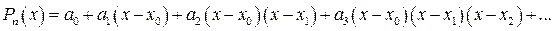
Коэффициенты полинома ai необходимо выразить через известные величины x0, h, n, yi (i = 0, 1, ... , n) пользуясь требованием (2.2), т.е. прохождением графика полинома через все точки заданной системы. Сразу заметим, что подстановка  в выражение (2.3) дает
в выражение (2.3) дает  . Следовательно, согласно (2.2), мы получаем значение свободного члена искомого полинома:
. Следовательно, согласно (2.2), мы получаем значение свободного члена искомого полинома:  . Остальные коэффициенты полинома Ньютона выразим через конечные разности.
. Остальные коэффициенты полинома Ньютона выразим через конечные разности.
Составим конечные разности первого порядка функции:

Из них, в свою очередь, таким же образом можно получить  конечных разностей второго порядка:
конечных разностей второго порядка:
 Аналогично определяются разности III и IV и т.д. порядков. Разность порядка
Аналогично определяются разности III и IV и т.д. порядков. Разность порядка  определяется формулой:
определяется формулой:
 ,
,
где  и
и 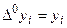 .
.
В некоторых случаях требуется знать выражения конечных разностей непосредственно через значения функции. Для нескольких первых порядков разностей их можно получить непосредственной подстановкой
 ;
;



Аналогично для любого  можно записать:
можно записать:
 .
.
Такую же формулу можно записать и для значения разности в узле  :
:
 .
.
Для функции  , заданной таблицей своих значений
, заданной таблицей своих значений  в узлах
в узлах 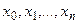 , конечные разности разных порядков удобно помещать в одну общую таблицу с узлами и значениями функции. Обычно используют горизонтальную таблицу или диагональную таблицу конечных разностей
, конечные разности разных порядков удобно помещать в одну общую таблицу с узлами и значениями функции. Обычно используют горизонтальную таблицу или диагональную таблицу конечных разностей
Интерполяционный многочлен Ньютона для заданной функции имеет вид
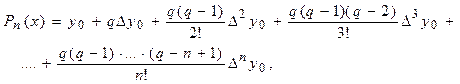 (2.4)
(2.4)
где  .
.
Анализ формулы (2.4) показывает, что погрешность построенного интерполянта Ньютона принимает наименьшие значения аргументов, близких к нулевому узлу x0. Примеры показывают, что не всегда целесообразно строить полином по всем узлам, так при этом могут возникать необоснованные «выбросы». В практических расчетах часто заранее выбирается степень интерполирующего полинома. Затем в качестве нулевого x0 берется узел, ближайший слева к значению аргумента x, для которого требуется вычислить значение неизвестной функции f(x). Интерполянт n-й степени (2.21) строится с помощью значений функции yi в узле x0 и в n узлах, расположенных правее аргумента x. Значения функции в узлах левее x0 не используются.
|
из
5.00
|
Обсуждение в статье: Классификация численных методов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

