Решение нелинейных уравнений

Решение уравнений – это одна из древнейших математических задач. Ещё в Древней Греции умели решать линейные и квадратные алгебраические уравнения. В эпоху Возрождения (XV век) Джироламо Кардано и его ученик Луиджи Феррари получили точные решения для алгебраических многочленов 3 и 4 степени. Позднее много усилий было затрачено на получение точного решения многочленов 5 степени и выше. Но только в 20-х годах XIX века было доказано, что решение алгебраического многочлена n-ой степени

a_n x ⁿ + a_n-1x^n-1 +...+ a₀ = 0, где   a_n ¹ 0

при n ³ 5 нельзя выразить через коэффициенты с помощью арифметических действий и операций извлечения корня.      

Известно, что алгебраический многочлен n-ой степени имеет n корней, причём они могут быть вещественными и комплексными (теорема Гаусса).

Рассмотрим вначале методы решения нелинейных уравнений с одним неизвестным. Пусть задана непрерывная f(x) и требуется найти корни уравнения

f(x) =0                                                                                         (2.12)

на всей числовой оси или на некотором интервале .

Выделяют две группы численных методов решения уравнений:

· прямые (формула Виета для квадратного уравнения и Кардано для кубического и другие)

· итерационные – для решения любого уравнения

Основные этапы решения. Решение задачи отыскания корней осуществляется в два этапа. Первый этап называется этапом отделения (локализации) корней, второй – этап итерационного уточнения корней.

   Известно, что если функция  непрерывна и принимает на концах отрезка  значения разных знаков, т.е. , то внутри этого промежутка имеется хотя бы один корень уравнения.

Геометрически это означает, что график непрерывной функции, расположенной по разные стороны оси , пересекает эту ось, по меньшей мере в одной точке.

Отрезок , содержащий только один корень уравнения , называется отрезком локализации корня. Цель этапа локализации считается достигнутой, если для каждых подлежащих определению корней удалось указать отрезок локализации.

К сожалению, создать универсальный метод локализации не представляется возможным. В простых ситуациях хороший результат может давать графический метод. Часто в качестве аналитического метода применяется метод Лагранжа локализации корней.

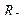    Пусть   - верхняя граница положительных корней полинома ,   - верхняя граница положительных корней ,   - верхняя граница положительных корней функции ,   - верхняя граница положительных корней функции .

Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида

f(x) = a₀x ⁿ + a₁x^n-1 +... + a_kx^{n- k} +…+ a_n , (a₀ >0)                       (2.14)

верхняя граница положительных действительных корней  определяется по формуле Лагранжа (Маклорена):

,                                                 (2.15)

где: k ³ 1 – меньший номер отрицательных коэффициентов полинома;

B – максимальный по модулю отрицательный коэффициент.

Все отличные от нуля действительные корни уравнения  (если они существуют) лежат внутри интервалов  и .

Приведем пример графического способа локализации корней уравнения

.

Для этого преобразуем уравнение к виду  и построим графики функций  и  (рис.2.5)

Абсциссы точек пересечения этих графиков являются корнями данного уравнения.

 

Рисунок 2.5. Графическое решение уравнений

 

Из рис.2.5 видно, что уравнение имеет два корня, расположенные на отрезках  и .

После локализации корней производится итерационное уточнение каждого корня одним из существующих методов. Мы рассмотрим метод касательных и метод итераций.

Метод касательных. Если известно хорошее начальное приближение решения уравнения , то эффективным методом повышения точности является метод Ньютона (метод касательных). Метод состоит в построении итерационной последовательности .

Достаточные условия сходимости этого метода содержатся в следующей теореме.

Теорема. Пусть функция  определена и дважды дифференцируема на отрезке , причем , а производные  сохраняют знак на отрезке . Тогда, исходя из начального приближения , удовлет-воряющего неравенству , можно построить последовательность  сходящуюся к единственному на  решению  уравнения .

Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой  касательной, проведенной в некоторой точке кривой (рис. 2.6).

  Выберем, например, , для которого . Проведем касательную к кривой  в точке 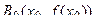. В качестве первого приближения  корня  возьмем абсциссу точки пересечения этой касательной с осью . Через точку  снова проведем касательную, абсцисса точки пересечения которой даст второе приближение  корня  и т. д. (рис. 2.6).

 

Рисунок 2.6. Геометрическая интерпретация метода Ньютона

 

Метод итераций. . Уравнение имеет действительный корень, лежащий в промежутке . Для уточнения его методом итераций приведем уравнение к виду . При этом должно выполняться условие  для . Функцию  будем искать из соотношения , считая, что , где  число  имеет тот же знак, что и  в промежутке .

 

                                          2.6. Численное интегрирование

Необходимость вычисления значений определенных интегралов при моделировании возникает достаточно часто. Формула Ньютона-Лейбница

                       (2.16)

имеет ограниченное применение, так как:

· не позволяет вычислить интегралы от таблично заданной подынтегральной функции f(x);

· не всякая подынтегральная функция имеет первообразную F(x).

Численные методы интегрирования универсальны: позволяют вычислить значение определенного интеграла непосредственно по значениям подынтегральной функции f(x), независимо от способа ее задания или вида аналитического выражения.

Геометрический смысл определенного интеграла – площадь криволинейной трапеции, ограниченной осью OX, кривой f(x) и прямыми x= a и x= b (Рис.2.7.).

 

 

Рисунок 2.7. Геометрический смысл определённого интеграла

 

Отрезок [a, b] делят на n необязательно равных частей – элементарных отрезков. Принято такое деление отрезка называть сеткой, а точки x₀, x₁,…, x_n – узлами сетки.

Если сетка равномерная, то  – шаг сетки, при интегрировании – шаг интегрирования, а координата i-го узла вычисляется по формуле:

                                                         (2.17)

Полная площадь криволинейной трапеции состоит из n элементарных криволинейных трапеций – элементарных площадей:

                                                                                (2.18)

Численные методы интегрирования основаны на различных способах оценки этой площади, поэтому полученные формулы численного интегрирования называются квадратурными (формулами вычисления площади). Квадратурные формулы отличаются друг от друга способом оценки значения S_i – площади элементарной криволинейной трапеции.

Рассмотрим получение и применение простейших формул.

Рассмотрим получение простейших формул для часто используемой равномерной сетки.

Формулы прямоугольников

Площадь i-той элементарной трапеции можно оценить (приближенно вычислить) как площадь прямоугольника со сторонами  и f_i. Тогда   и значение интеграла:

(2.19)

 

Рисунок 2.8. Оценка элементарной площади S_i левым прямоугольником.

 

Полученная формула называется формулой левых прямоугольников, т.к. для оценки площади использовалось левое основание элементарной криволинейной трапеции.

Аналогично можно получить формулу правых прямоугольников:

 

 

Рисунок 2.9. Оценка элементарной площади S_i правым прямоугольником.

 

Для данного случая  и тогда значение интеграла:

(2.20)

Эти формулы не находят широкого применения, т.к. имеют большую погрешность, пропорциональную величине шага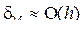

Как появляется эта погрешность, видно на рисунках.

Для повышения точности площадь S_i можно оценить, используя прямоугольник со стороной, равной значению подынтегральной функции в середине элементарного отрезка

Для данного случая  и формула центральных прямоугольников имеет вид:

    (2.21)

 

Рисунок 2.10. Оценка элементарной площади S_i центральным прямоугольником.

 

Как видно из рис. 2.10, погрешность в оценке площади S_i в данном случае существенно меньше, чем в двух предыдущих (погрешность оценивается разницей площадей δ₁ и δ₂).

Погрешность метода пропорциональная квадрату величины шага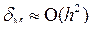

Для повышения точности необходимо увеличить n или использовать более точные квадратурные формулы.

Формула трапеции

В данном методе элементарная криволинейная трапеция заменяется трапецией (кривая f(x) заменяется хордой CD).

Рисунок 2.11. Оценка элементарной площади S_i трапецией.

 

Из рисунка видно, что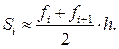

Отсюда:

                   (2.22)

Погрешность формулы трапеций пропорциональная квадрату шаг h  т.е. формулы центральных прямоугольников и трапеций имеют близкую точность.

Формула трапеций имеет такую же точность, как и формула центральных прямоугольников. Абсолютная погрешность метода трапеций оценивается как.

 

 

Метод Симпсона

Метод Симпсона применим при разбиении интервала  на четное число частей . Каждая пара полосок ограничивается сверху параболой, проходящей через три точки. Затем вычисляется площадь каждой пары полосок, ограниченной сверху параболой. Сумма площадей всех пар полосок является приближенным значением определенного интеграла (рис. 2.12).

 

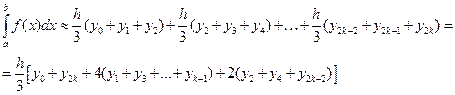
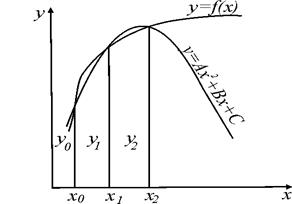
Рисунок 2.12. Метод Симпсона