Численное решение дифференциальных уравнений

Уравнение, содержащее производные от искомой функции y = y(x), называется обыкновенным дифференциальным уравнением (ОДУ). Общий вид дифференциального уравнения:

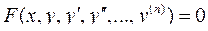                                                         (2.23)

где n – наивысший порядок производной, определяет порядок уравнения.

Решением ОДУ называется функция y= y(x), которая после ее подстановки в уравнение (2.23) обращает его в тождество.

Общее решение ОДУ имеет вид:

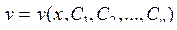                                                                (2.24)

где C₁, C₂, …, C_n – постоянные интегрирования.

Частное решение получается из общего при конкретных значениях C_i, 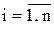. Эти значения определяются из n дополнительных условий. В качестве таких условий могут быть заданы значения функции и ее производных при некоторых значениях аргумента x, иначе говоря, в некоторых точках.

В зависимости от того, как заданы эти дополнительные условия, выделяют 2 типа задач:

· задача Коши. Все условия заданы в одной, начальной точке, поэтому они называются начальными условиями.

· краевая задача. Условия заданы в более чем одной точке, обычно в начальной и конечной. Условия в этом случае называются краевыми или граничными. Такая задача может возникнуть только при решении ОДУ с порядком выше первого.

Разработано множество методов решения подобных задач:

1. Графические методы. Например, метод изоклин – путем графических построений находят точки исходной функции и строят ее график.

2. Аналитические методы позволяют получить формулу исходной функции путем аналитических преобразований.

3. Приближенные методыпозволяют получить приближенное аналитическое решение в результате принятых упрощений. К приближенным относятся асимптотические методы и метод малых возмущений.

4. Численные методы позволяют получить таблицу приближенных значений искомой функции для ряда заранее выбранных значений ее аргумента.

На практике чаще всего применяются численные методы: они просты в использовании и не имеют ограничений.

Задача решения ОДУ 1-го порядка (задача Коши) формулируется следующим образом:

Найти y= y(x), удовлетворяющую уравнению

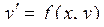                                                                              (2.25)

для 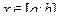 при заданном начальном условии y(a) = y₀.

Рассмотрим численные методы решения этой задачи.

Метод Эйлера (метод Рунге-Кутта 1-го порядка).

Разобьем отрезок [a, b] на n необязательно равных частей – элементарных отрезков, точки x₀, x₁,…, x_n – узлы сетки, если сетка равномерная, то 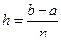 – шаг сетки Очевидно, что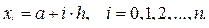

Заменим в уравнении (2.25) 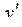 в точке x_i  её приближенной оценкой – отношением приращений (это следует из определения производной):

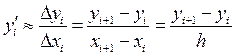
Тогда получаем:

.

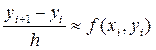Отсюда формула Эйлера:

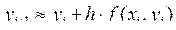                                       (2.26)

Зная y₀ в точке x₀ (начальное условие) можно найти y₁, затем, используя уже известные значения x₁ и y₁, вычислить x₂ и y₂ и так далее.

Рассмотрим геометрическую иллюстрацию метода Эйлера. В координатах (x,y) отобразим известные данные: отрезок [a,b] на оси ОХ и начальное условие y₀ – точка А с координатами (a, y₀). Отрезок [a,b] разобьем на n равных частей, получим узлы равномерной сетки a = x₀, x₁, x₂, … , x_n = b. Вычислим значения первой производной искомой функции в точке А, используя координату этой точки и исходное уравнение (2.25)

.

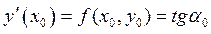Полученное значение позволяет построить касательную к искомой функции в точке А. Эту касательную можно использовать для вычисления приближенного значения искомой функции в новом узле х₁ (кривую y(x) заменяем на отрезком АВ на элементарном отрезке [x₀, x₁]).

Рисунок 2.13. Геометрическая иллюстрация метода Эйлера.

Зная (x₁,y₁), можно аналогично получить новую точку (x₂,y₂) и т.д.

Из геометрической иллюстрации следует, что:

1. на каждом шаге есть погрешность (на рисунке это отрезок BD). Погрешность тем больше, чем больше шаг.

2. ошибка может накапливаться.

Формула Эйлера (2.26) имеет погрешность метода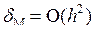

Для практического выбора h с целью обеспечения заданной точности решения задачи e применяется следующий прием.

Выполняются два расчета: с n и 2n узлами. Если полученные значения функции во всех узлах отличаются не более чем на e, задача считается решенной. Если нет, число узлов вновь удваивают и опять сравнивают полученные значения функций.

Таким образом, расчет продолжается до достижения условия

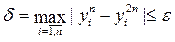
Значение n может достигать большой величины – более 1000. Чтобы не печатать столько значений функции, в алгоритме решения ОДУ методом Эйлера нужно предусмотреть печать не всех рассчитанных значений, а только части их, например, десяти значений, распределенных равномерно по всему отрезку.