Общее решение волнового уравнения в случае одной пространственной переменной. Решение Даламбера

Рассматривая решения обыкновенных дифференциальных уравнений в курсе высшей математики, мы видели, что общее решение содержало произвольные постоянные. Например, общее решение дифференциального уравнения

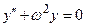
имеет вид

,

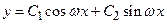где 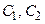, произвольные константы, которые могут принимать любые значения из интервала (-∞, + ∞) или даже комплексные значения.

В отличие от обыкновенных дифференциальных уравнений, общее решение дифференциального уравнения с частными производными, как увидим ниже, содержит уже не произвольные постоянные, а произвольную функцию.

Рассмотрим решение одномерного волнового уравнения, описывающего свободные колебания однородной струны

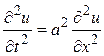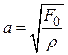, ,                                            (1.31)

где 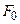 – сила натяжения, действующая на струну,  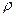– постоянная линейная плотность струны,  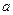– постоянная с размерностью скорости, .

Запишем уравнение (1.31) в виде

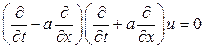                                         (1.32)

и введем новую функцию

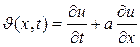 .                                              (1.33)

Уравнения (1.32) и (1.33) образуют систему дифференциальных уравнений в частных производных первого порядка, эквивалентную уравнению (1.31):

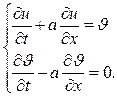                                                  (1.34)

Первое из этих уравнений является неоднородным дифференциальным уравнением. Второе уравнение, получаемое из уравнения (1.32) с помощью замены (1.33), является однородным уравнением (”без правой части”). Для решения системы уравнений (1.34) нужно решить сначала второе уравнение, а затем – первое, подставив в правую часть найденную функцию .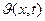

Разыскиваем решение второго уравнения системы (1.34) в виде , где 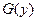 – произвольная функция, имеющая производную по аргументу . Используя правило дифференцирования сложной функции, получаем:

где штрих означает производную по аргументу. Подставляя полученные выражения для частных производных во второе уравнение системы (1.34), убеждаемся, что функция 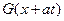 является его решением

.

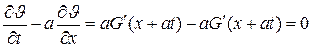Таким образом, доказано, что произвольная дифференцируемая функция  является решением этого уравнения.

Для решения первого уравнения системы (1.34) удобно вместо функции 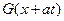 ввести другую функцию с помощью соотношения

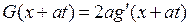.                                (1.35)

В соответствии с этой заменой первое уравнение системы (1.34) запишется в виде

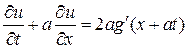.                                (1.36)

Преобразуем теперь уравнение (1.36) так, чтобы оно стало однородным дифференциальным уравнением для новой неизвестной функции, введенной вместо функции 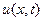. Для этого заметим, что производные функции  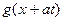по временной и пространственной переменным имеют вид:

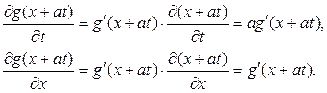
 Поэтому уравнение (1.36) можно записать в виде

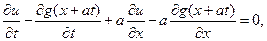
или, объединяя члены с производными по одинаковым переменным,

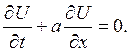                                      (1.37)

Здесь новая неизвестная функция выражается через старую и введенную соотношением (1.35) функцию следующим образом

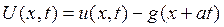.                                       (1.38)

Уравнение (1.37) имеет такой же вид, как и второе уравнение системы (1.34), но с заменой постоянной 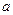 на (- ). Поэтому его решением является произвольная дифференцируемая функция .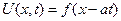

Теперь из соотношения (1.38) можно получить общее решение первого уравнения системы (1.34)

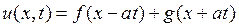,                                                (39)

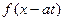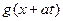где  и – произвольные дважды непрерывно дифференцируемые функции.

Поскольку первое уравнение системы (1.34) является уравнением (1.32), равносильным уравнению (1.31), то заключаем, что формула (1.39) дает общее решение волнового уравнения в одномерном случае.

Формула (1.39) называется решением Даламбера одномерного волнового уравнения. Она была получена Даламбером в 1747 году.

Физический смысл решения Даламбера

Рассмотрим сначала решения уравнения вида 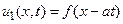. Пусть наблюдатель выходит в начальный момент  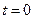из точки  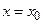и передвигается в положительном направлении оси ОХ со скоростью 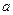. Пройденный наблюдателем путь за время t равен  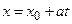или 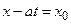. Для этого наблюдателя смещение струны – постоянно. Все время своего движения наблюдатель видит одно и то же смещение струны. Таким образом, функция 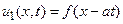 описывает распространение смещения струны вдоль положительного направления оси ОХ. Это решение называется прямой волной,  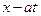называется фазой прямой волны.

Аналогично, функция 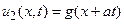 называется обратной волной,  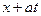– фазой обратной волны. Эта функция описывает распространение смещения струны в отрицательном направлении оси ОХ со скоростью .

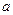Таким образом, сумма прямой и обратной волн представляет собой общее решение однородного волнового уравнения в одномерном случае. В этом и заключается физическое содержание решения Даламбера (1.39).

Отсюда вытекает следующий графический способ построения формы струны в любой момент времени:

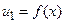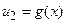Строим кривые  и  при ;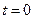

1. Не меняя формы этих линий, передвигаем их со скоростью 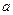 в разные стороны —  вправо, 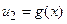 влево;

2. Для получения графика формы струны в момент времени t строим алгебраические суммы раздвинутых кривых в данный момент времени.