Понятие уравнения в частных производных и его решения. Основные уравнения математической физики

СПЕЦИАЛЬНЫЕ ГЛАВЫ МАТЕМАТИКИ

 

Учебно-методическое пособие

Для студентов направления подготовки «Нефтегазовое дело»

Семестр

Воронеж, 2019

 

УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

Понятие уравнения в частных производных и его решения. Основные уравнения математической физики

Уравнение, связывающее неизвестную функцию , независимые переменные  и частные производные от функции  называется дифференциальным уравнением с частными производными

                       (1.1)

где – заданная функция своих аргументов.

   Порядок старшей производной, входящей в уравнение (1.1), называется порядком уравнения с частными производными.

   Уравнение с частными производными называется квазилинейным, если оно линейно относительно всех старших производных от неизвестной функции. Например, уравнение

является квазилинейным уравнением второго порядка, - заданные функции.

Уравнение с частными производными называется линейным, если оно линейно и относительно неизвестной функции, и относительно ее частных производных. Примером линейного уравнения второго порядка является уравнение

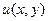где  - заданные функции, - неизвестная функция.

Решением уравнения с частными производными (1.1) называется всякая функция 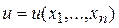, которая, будучи подставлена в уравнение вместо неизвестной функции и ее частных производных, обращает это уравнение в тождество по независимым переменным.

   Например, уравнение

имеет решение , где 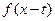 - любая дифференцируемая функция.

   Многие задачи математики, физики, различных областей техники приводят к исследованию дифференциальных уравнений с частными производными второго порядка. Удивительно то, что весьма многие задачи из разных отраслей знания приводят к одним и тем же уравнениям.

Из всех известных уравнений с частными производными, наиболее часто встречающимися при описании различных физических явлений и наиболее хорошо изученными математиками, являются уравнения, названные основными уравнениями математической физики.

Математическая физика – это область феноменологической физики, работающей с идеей непрерывных сред, в противоположность атомистической физики, выдвинувшейся на передний план в начале 20-го века.

Перечислим основные уравнения математической физики.

Обозначим через  – пространственные декартовы координаты точки, через  – время,  – заданную функцию,  – заданную постоянную (имеющую в каждом уравнении свой физический смысл),  – неизвестную функцию,  – оператор Лапласа

Тогда основные уравнения математической физики записываются в следующем виде:

1. Уравнение Лапласа

.

Потенциалы поля тяготения и стационарного электрического поля (в котором отсутствуют массы и электрические заряды)

удовлетворяют этому уравнению. Оно описывает также потенциальное течение жидкости, потенциал стационарного тока и другие явления;

2. Уравнение Пуассона

описывает установившееся тепловое состояние однородного и изотропного твердого тела при наличии источников тепла, потенциал электрического поля при наличии зарядов и др.;

3. Уравнение теплопроводности

описывает процессы распространения тепла в однородном изотропном теле, а также явление диффузии газов;

4. Волновое уравнение

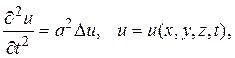
описывает распространение упругих, звуковых и электромагнитных волн, а также другие колебательные явления.

 

1.2. Уравнения современной математической физики

Кроме классических уравнений математической физики известны и другие уравнения, которые изучались уже в 20-ом столетии и которые имеют первостепенное значение и для науки, и для технических приложений. К таковым относятся:

1. Уравнение Шредингера

описывает движение субатомных частиц в поле потенциала , где  - комплексная функция, квадрат модуля которой определяет плотность вероятности нахождения частицы в данный момент времени в точке

2. Уравнение Синус - Гордона

описывает квантовые поля, самоиндуцированную прозрачность идеального диэлектрика при взаимодействии его с электромагнитным полем на резонансных частотах, двумерные поверхности с постоянной отрицательной кривизной, описывает также солитоны – уединенные волны, ведущие себя подобно обычным частицам и т.д.;

3. Уравнение Кортевега - де Фриза

описывает уединенные волны на поверхности жидкости, плазменные волны, слабонелинейные магнитогидродинамические волны и другие процессы.

4. Уравнение Бюргерса

описывает турбулентное течение, звуковые волны в вязкой среде, магнитогидродинамические волны в среде с конечной электропроводимостью и другие явления.

 

1.1.1. Уравнение Шредингера

Основная идея волновой механики заключается в том, что для таких малых тел, как электрон, нельзя с определенностью сказать, где оно находится в данное время и куда направляется. Можно установить только относительную вероятность его нахождения в том или ином месте и наличие определенного количества движения в определенный момент времени. В соответствии с волновой механикой какая-либо система – атом, молекула, электрон и т.д. – описывается функцией состояния или волновой функцией, обозначаемой  («пси»), которая является функцией координат всех частиц, образующих эту систему. Следовательно, величина  зависит только от положения всех частиц в пространстве. В 1924 г. де Бройль предположил, что точно также, как свет, который, как обычно считают, имеет волновую природу, на самом деле при определенных обстоятельствах ведет себя, как будто он состоит из частиц – квантов, – так и очень малые частицы, такие, как электроны, также могут обладать волновыми свойствами. Де Бройль предположил, что с пучком электронов следует связывать длину волны, определяемую уравнением

                                                                             (1)

где  – постоянная Планка (  Дж  с ), а  – количество движения (импульс) электрона в пучке, т.е. его масса, умноженная на его скорость. Физическое подтверждение волновой природы электрона было продемонстрировано в 1927 – 1928 гг. Дейвиссоном, Джермером и Томсоном, которые показали, что пучок электронов может испытывать дифракцию на подходящей решетке (атомы в кристалле золота), аналогичную дифракции пучка света.

 

Рисунок 1.1.  Дифракция пучка электронов

 

На преграду с двумя узкими щелями направлен параллельный пучок моноэнергетических (т.е. обладающих одинаковой кинетической энергией) электронов (рис. 1. а). За преградой находится фотопластина . При закрытии щели номер 2 и экспонировании в течение времени t почернение на проявленной фотопластине будет характеризоваться кривой 1 (рис. 1. б). При закрытии щели номер 1, соответственно, почернение на фотопластине будет соответствовать кривой 2. Однако в случае, когда открыты обе щели картина почернения фотопластины (рис. 1. в) отнюдь не эквивалентна наложению двух первых картин. Зато она аналогична картине, получающейся при интерференции двух когерентных световых волн.

Тот факт, что системы малых частиц проявляют, по крайней мере, при определенных условиях, волновые свойства, предполагает возможность описания таких систем уравнениями, подобными те, которые описывают другие виды волнового движения, например, волны, которые распространяются вдоль колеблющейся струны, или волновое движение, приписываемое электромагнитному излучению. Действительно, можно начать с волнового уравнения, соответствующего электромагнитным волнам, и путем определенных замен, превратить его в уравнение, соответствующее нашему случаю. Хотя эти замены диктуются физическими причинами, они в основном произвольны и могут быть приняты только потому, что приводят к уравнению, которое, как показывает опыт, позволяет получить правильное решение физических задач. Поэтому следует принять волновое уравнение как постулат, так как у химиков основной интерес вызывает применение волнового уравнения к атомным и молекулярным системам, а не физические и математические соображения, которыми руководствовался Шредингер, впервые его предложивший в 1925 г.

Рисунок 1.2. Эрвин Шрёдингер (1887 - 1961)

 

Согласно фольклору, распространенному среди физиков, случилось это так: в 1924 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны – они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики – и с блеском справился с этой задачей.

Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) – в такой передаче энергии участвуют частицы – или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа – корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений – волновыми уравнениями. Все без исключения волны – волны океана, сейсмические волны горных пород, радиоволны из далеких галактик – описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности, эти волны также должны описываться соответствующим волновым уравнением.

Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому, как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица.

Приведем уравнение Шрёдингера в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой ψ, является решением следующего дифференциального уравнения:

,

где x – расстояние, h – постоянная Планка, а m, E и U – соответственно масса, полная энергия и потенциальная энергия частицы.

Волновое уравнение, применяемое для расчета стационарных состояний системы, можно записать в символическом виде:

                                          (1)

где H представляет собой определенный способ выражения общей энергии системы, а E – числовое значение этой энергии. Для всех систем, которые обычно интересуют химиков, общая энергия представляет собой сумму кинетической энергии Т и потенциальной энергии U:

H= T+ U                                             (2)

Это соотношение было широко использовано физиком-теоретиком Гамильтоном, поэтому H часто называют функцией Гамильтона, а 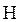 – гамильтонианом системы.

Рассмотрим уравнение Шредингера на примере атома водорода. Модель атома водорода предложил Бор. Для простоты предположим, что тяжелое ядро закреплено (оно почти, но не совершенно неподвижно, когда электрон движется вокруг него). Тогда полная кинетическая энергия Т системы представляет собой просто кинетическую энергию электрона

 ,                                                   (3)

где m – масса электрона и v – его скорость. Потенциальная энергия системы есть просто энергия, возникающая вследствие электростатического взаимодействия (гравитационные силы приблизительно в раз меньше), и ее можно выразить как

 ,                                                   (4)

где e – заряд электрона, r – радиус орбиты, знак минус появляется вследствие того, что заряд одной из частиц положителен (+), а другой отрицателен (-). Поэтому для атома водорода функция Гамильтона в классической (т.е. доквантовомеханической) физике равна:

 ,                                                   (5)

 Если использовать понятие количества движения электрона p= mv, данное уравнение запишется в следующем виде:

 ,                                                   (6)

Теперь для перехода от классического описания этой или какой-либо другой системы к описанию при помощи волновой механики, необходимо взять функцию Гамильтона (уравнение 6) и произвести в ней определенные замены: в функции Гамильтона количество движения p следует заменить выражением

 ,                                                   (7)

Таким образом, гамильтониан для атома водорода в его квантовомеханической форме следует записать в виде

.                                (8)

Если теперь это выражение гамильтониана подставить в общее волновое уравнение (уравнение 1), то получим:

.                            (9)

Это и есть волновое уравнение для атома водорода.

Если найдена функция , то говорят, что она является решением волнового уравнения, и ее называют волновой функцией. Вообще, может быть несколько различных функций , , ... , , которые являются решениями уравнения 9, причем каждой соответствует свое значение энергии Е₁, Е₂, ... , Е _n.

Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.

Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа Вернера Гейзенберга, в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий – то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче изучать.

Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч – это частица, звук – это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле – и эксперименты это вскоре показали – в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны.

Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира. В микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, – яркое тому доказательство. В этом нет особого противоречия, ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей

1.1.2. Уравнение  синус – Гордона

За последние десятилетия в теоретической физике при исследованиях нелинейных волновых процессов наблюдается бурный прогресс, характеризуемый рядом фундаментальных достижений. Одним из таких достижений бесспорно является прогресс в изучении динамики солитонов – уединенных частице подобных устойчивых волн, способных распространяться с постоянной скоростью и упруго взаимодействовать с себе подобными волнами. Специальные решения, способные описывать поведение подобных волн, были открыты для ряда нелинейных дифференциальных уравнений в частных производных, часто называемых также «солитонными» уравнениями, одним из самых известных пред-ставителей которых является уравнение синус-Гордона (УСГ). Замечательным свойством данного уравнения является его полная интегрируемость.

Уравнение синус-Гордона описывает такие физические явления и процессы,  как распространение импульсов в двухуровневых резонансных средах, технологию сверхдальней связи по оптическим линиям, поведение блоховски хстенок в ферромагнитных кристаллах, движение дислокаций, процессы в джозефсоновских контактах, описание нелинейных эффектов в геофизических средах и ряд других физических явлений. Лишь в 1936 г. немецкий математик Штойервальд нашел решения, соответствующие по современным критериям одному, двум солитонам и бризеру. Впервые в физику его ввели в 1938 г. Я. И. Френкель и Т. М. Канторова как уравнение, описывающее распространение дислокаций в одномерном кристалле. В настоящее время уравнение синус-Гордона широко используется в геометрии сейсмологии, в оптике и биологии (Скотт, 2007; Браун, Кившарь, 2008; Аэро и др., 2009), в физике и метеорологии. Каждая из этих наук по-своему подошла к открытию уравнения синус-Гордона, но, открыв, стала активно его использовать и находить все новые и новые стороны его применения, а также его модификаций.

Однако в сейсмологии и геомеханике (наиболее актуальных для специалистов в нефтегазовой области) уравнение sin-Гордона применено относительно недавно при моделировании сейсмических и деформационных процессов, обусловленных вращением блоков в фрагментированной геологической среде (Николаевский, 1995; Гарагаш, 1996; Гарагаш, Николаевский, 2009).

Исчерпывающие сведения об уравнении sin-Гордона, его решениях и их свойствах можно найти в замечательных монографиях и статьях [Уизем, 1977; Лэм, 1983; Додд и др., 1988; Kivshar, Malomed 1989; Braun, Kivshar, 1998; Браун, Кившарь, 2008].

Приведены только те решения уравнения sin-Гордона, которые использованы при построении моделей сейсмической активизации разломов и отражают основные черты процесса деформирования разломных зон, и относительную роль различных факторов в волновой динамике очага землетрясений. Рассмотрим основные модели деформационных процессов в земной коре, соответствующие классическому уравнению sin-Гордона.

Классическое уравнение sin-Гордона имеет вид

                                (1)

где t , x – временная и пространственная координаты; u – динамическая переменная (угол поворота или смещение блока (фрагмента) среды). Если искать решение в виде бегущей волны (β — скорость волны)

то уравнение (1) переходит в

                                               (2)

Уравнение (2) имеет следующие общеизвестные решения:

1) периодические быстрые кноидальные волны

2) периодические медленные кноидальные волны;

3)  уединенные волны –  солитоны, перемещающиеся со скоростью β;

4) уединенные волны –  кинки, волны с неизменным профилем в виде перегиба по переменной u;

t

t

t

Рисунок 1.3 . Профили скоростей V частиц в «быстрой» (1) и «медленной» (2) кноидальных и уединенной (3) волнах, смещениягu частиц (4) — кинк.

 

Поиски аналогий и построение новых (именно нелинейных) математических моделей деформирования разломных и фрагментированных геологических сред были мотивированы невозможностью объяснить наблюдаемые эффекты в рамках линейной теории упругости (вязкоупругости или упругопластичности).

Математическая модель поворотных колебаний блоков в разломах земной коры, генерирующих деформационные волны, впервые предложена В.Н. Николаевским [Николаевский, 1995]. Исследование таких волн имеет принципиальное значение для выявления механизмов миграции как предвестников землетрясений в земной коре [Nikolaevskiy, 1998], так и крупномасштабных тектонических волн [Михайлов, Николаевский, 2000]. Соответствующее данному механизму уравнение синуса-Гордона дает решение в виде медленно распространяющейся тектонической волны солитонного типа – кинка.

В статье [Wu, Chen, 1998] на основе одномерной пружинно-блоковой модели Барриджа-Кнопова получено классическое уравнение синуса-Гордона и показана возможность применения его решения в виде уединенной волны (кинка) для исследования землетрясений. Из решения следует, что скорость распространения волны всегда меньше скорости сейсмических волн.

Ротационная модель сейсмического процесса, в которой возбуждение волн деформации в цепочке сейсмофокальных блоков связано с вращением Земли вокруг собственной оси, представлена в [Викулин, 2008]. Показано, что уравнение синуса-Гордона объясняет некоторые особенности сейсмического процесса.

Совсем недавно решение уравнения синуса-Гордона в виде медленных кноидальных волн – последовательности импульсов с некоторым пространственным периодом – применено при математическом моделировании динамики деформационных процессов на границе плит в зонах трансформных разломов и связанных с этим эффектов [Gershenzon et al., 2009]. Модель количественно описывает основные стадии сейсмического процесса и медленные землетрясения. В статье [Gershenzon et al., 2011] на основе классического уравнения синуса-Гордона проведено моделирование особенностей динамики литосферных плит и зон субдукции, и интенсивно изучаемых в настоящее время медленного скольжения и миграции сейсмического тремора.

Вторая проблема, успешно развиваемая с применением уравнения синуса-Гордона, связана с исследованием тектонической активности особого типа – «медленных землетрясений». Медленное скольжение по разлому и сейсмический тремор (episodic tremor and slow slip – ETS), сопровождающие «медленные

землетрясения», наблюдались в Тихоокеанских зонах субдукции, в разломе Сан-Андреас [Schwartz, Rokosky, 2007]. ETS возникают с замечательной регулярностью: в различных зонах субдукции интервал повторяемости составляет от 3 до 18 мес. Миграция тремора вдоль разломов происходит со скоростью, изменяющейся от 5 до 16 км/сут, и в среднем равна 10 км/сут [Rogers, Dragert, 2003]. Что контролирует скорость миграции тремора и почему в различных зонах субдукции, удаленных друг от друга на многие тысячи километров, скорости миграции практически одинаковы, а интервал повторяемости существенно различный? Можно ожидать, что ответы на эти вопросы и построение адекватного механизма миграции ETS связаны, прежде всего, с установлением причин периодичности их возникновения и миграции ETS со скоростью порядка 10 км/сут.

Тремор и медленное скольжение, развивающиеся на границе плит в зонах субдукции и трансформных разломов, могут служить новым проявлением и признаком деформационных волн Земли. Несмотря на большие успехи в теоретических исследованиях, здесь остаются проблемы, требующие дальнейшего развития и анализа. Представленные в обзоре механизмы генерации деформационных

волн еще недостаточно разработаны, для точного расчета динамических характеристик этих волн следует определить реальные значения ряда введенных в модели параметров.

Дальнейшее математическое моделирование деформационных волн Земли с применением уравнения синуса-Гордона необходимо для определения оптимальных условий их наблюдения, выявления основных физических механизмов, вызывающих сейсмическую миграцию и генерацию сигналов различного происхождения, сопровождающих волны деформации на различных масштабных уровнях.

 

1.1.3. Уравнение Кортевега - де Фриза

Первое наблюдение уединенной волны в 1834г. сделал шотландский ученый и инженер Дж. Скотт Рассел (1808–1882). Окончив Университет Глазго в 16 лет, он работал в Отделении естественной истории в Эдинбурге, где изучал пропускную способность канала Юнион. Вот в процессе этих исследований он доложило следующем: «Я наблюдал за движением баржи, которую быстро тащила вдоль узкого канала пара лошадей, когда внезапно баржа остановилась – вся масса воды в канале пришла в движение; вода собралась у носа корабля в состоянии бурного волнения, затем вдруг оторвалась от него и покатилась вперед с большой скоростью, приняв вид большого уединенного возвышения; округлый, гладкий, четко выраженный холм воды продолжал свое движение по каналу без видимого изменения формы или уменьшения скорости. Я бросился за этой волной верхом на лошади и догнал ее, когда она все еще двигалась со скоростью около восьми или девяти миль в час, сохраняя первоначальную форму, и имела около тридцати футов в длину и от фута до полутора футов в высоту. Ее высота постепенно уменьшалась, и после одной или двух миль погони я потерял ее в изгибах канала. Так в августе месяце 1834 г. произошла моя первая встреча с этим необыкновенным и прекрасным явлением, которое я назвал Волной Переноса (The Wave of Translation)».

Работа Рассела, опубликованная в 1844 году как "Доклад о волнах", вызвала осторожную реакцию в среде ученых. На континенте ее не заметили совсем, а в самой Англии на нее обратили внимание Г.Р. Эйри и Дж.Г. Стоке. Эйри подверг критике результаты экспериментов, которые наблюдал Рассел. Он отмечал, что из теории длинных волн на мелкой воде выводы Рассела не получаются, и утверждал, что длинные волны не могут сохранять неизменную форму. И в конечном итоге подверг сомнению правильность наблюдений Рассела. Один из основателей современной гидродинамики, Джордж Габриэль Стоке, также не согласился с результатами наблюдений, полученными Расселом, и критически отнесся к факту существования уединенной волны.

После столь негативного отношения к открытию уединенной волны долгое время о ней просто не вспоминали. Определенную ясность в наблюдения Рассела внесли Дж. Буссинеск (1872 год) и Дж.У. Рэлей (1876 год), которые независимо друг от друга нашли аналитическую формулу для возвышения свободной поверхности на воде в виде квадрата гиперболического секанса и вычислили скорость распространения уединенной волны на воде.

В 1872 г. Жозеф  Буссинеск  предложил уравнение, описывающее длинные волны на поверхности жидкости и показал, что оно имеет решение типе уединенной волны:

 

Однако, скорость этой волны входит параметром в само уравнение.

Дидерик Иоханнес Кортевег – нидерландский математик, выполнивший первые работы по исследованиюуравнения Кортевега – де Фриза.  Д. Кортевег родился в семье судьи в городе Хертогенбос. Начинал свое обучение в Делфтской политехнической школе, собираясь стать инженером, однако впоследствии любовь к математике заставила его бросить учебу и стать школьным учителем математики. В 1878 году получил диплом доктора философии в Амстердамском университете с дипломной работой, посвященной распространению волн в эластичных трубах. С 1881 по 1918 годы Кортевег работал в Амстердамском университете в качестве профессора математики, механики и астрономии. В это время совместно со своим студентом Густавом де Фризом им была опубликована его самая известная работа «On the Change of Form of Long Waves advancingin a RectangularCanal and on a New Type of Long Stationary Wave».

Густав де Фриз – нидерландский матема-тик, известный тем, что первым исследовал уравнение Кортевега–де Фриза. Родился в Амстердаме. Учился в Амстердамском университете. В 1894 году под руководством Дидерика Кортевега защитил докторскую по теме «Bijdrage tot de kennis der lange golven» («Вклад в знания о длинных волнах»). На следующий год вышла его совместная с руководителем классическая работа, в которой было предложено уравнение, называемое с тех пор уравнением Кортевега–де Фриза. Эта работа стала крупнейшим достижением ученого. Впоследствии де Фриз работал преподавателем математики в высшей школе в Харлеме. В 1931 году ушел в отставку. В 1895г. Кортевег и де Фриз получили уравнение распространения волн в одном направлении по поверхности мелкого канала (для невязкой, несжимаемой, однородной жидкости в постоянном поле тяжести)

Они показали, что это уравнение обладает уединенной волной, т.е. решением вида

.

Именно эту волну и наблюдал Рассел.

В настоящее время кажется странным, что открытие Рассела и его последующее подтверждение в работе Кортевега и де Фриза не получили заметного резонанса в науке. Эти работы оказались забытыми почти на 70 лет. Один из авторов уравнения, Д.Д. Кортевег, прожил долгую жизнь и был известным ученым. Но когда в 1945 году научная общественность отмечала его 100-летний юбилей, то в списке лучших публикаций работа, выполненная им с де Фризом, даже не значилась. Составители списка сочли эту работу Кортевега не заслуживающей внимания. Только спустя еще четверть века именно эта работа стала считаться главным научным достижением Кортевега.

Однако если поразмыслить, то такое невнимание к уединенной волне Рассела становится понятным. Дело в том, что в силу своей специфичности это открытие долгое время считалось довольно частным фактом. В самом деле, в то время физический мир казался линейным и принцип суперпозиции считался одним из фундаментальных принципов большинства физических теорий. Поэтому никто из исследователей не придал открытию экзотической волны на воде серьезного значения.

Возвращение к открытию уединенной волны на воде произошло в какой-то степени случайно и вначале, казалось, не имело к нему никакого отношения. Виновником этого события стал величайший физик нашего столетия Энрико Ферми. В 1952 году Ферми попросил двух молодых физиков С. Улама и Д. Паста решить одну из нелинейных задач на ЭВМ. Они должны были рассчитать колебания 64 грузиков, связанных друг с другом пружинками, которые при отклонении от положения равновесия приобретали возвращающуюся силу. Создавая начальное колебание, исследователи хотели посмотреть, как эта начальная мода будет распределяться по всем другим модам. После проведения расчетов этой задачи на ЭВМ ожидаемого результата они не получили, но обнаружили, что перекачивание энергии в две или три моды на начальном этапе расчета действительно происходит, но затем наблюдается возврат к начальному состоянию. Об этом парадоксе, связанном с возвратом начального колебания, стало известно нескольким математикам и физикам. В частности, об этой задаче узнали американские физики М. Крускал и Н. Забуски, которые решили продолжить вычислительные эксперименты с моделью, предложенной Ферми.

После расчетов и поиска аналогий эти ученые установили, что уравнение, которое использовали Ферми, Паста и Улам, при уменьшении расстояния между грузиками и при неограниченном росте их числа переходит в уравнение Кортевега–де Фриза. То есть по существу задача, предложенная Ферми, сводилась к численному решению уравнения Кортевега–де Фриза, предложенного в 1895 году для описания уединенной волны Рассела. Примерно в те же годы было показано, что для описания ионно-звуковых волн в плазме используется также уравнение Кортевега–де Фриза. Тогда стало ясно, что это уравнение встречается во многих областях физики и, следовательно, уединенная волна, которая описывается этим уравнением, является широко распространенным явлением.

Продолжая вычислительные эксперименты по